Aire d’un polygone irrégulier

Cet article décrit une solution simple à un problème géométrique, un problème que je trouve décrit de manière trop complexe en ligne. Le problème consiste à calculer l’aire et la longueur du périmètre d’une figure fermée bidimensionnelle comme le plan d’une pièce, ou une parcelle de terrain, ou toute autre figure délimitée bidimensionnelle (un « polygone irrégulier »), quelle que soit sa complexité.

Je ne revendique certainement pas l’originalité de cette méthode. Des versions existent depuis l’époque de Gauss ou avant. Mais la plupart des articles en ligne décrivent la méthode de manière inutilement complexe. Les références incluent l’article Wikipedia Shoelace Formula, une méthode aussi complexe dans l’article Polygon, et un certain nombre d’articles qui semblent calculés plus pour démontrer l’érudition de l’auteur que pour fournir l’incarnation la moins complexe de la méthode. Cet article (PDF) montre l’une des expressions les moins complexes (mais en aucun cas simples) :

(1) $A = \frac{1}{2} \x_0 & x_1 \\\N y_0 & y_1\N\N\N\N\N- fin{array} \N-right| + \N-ft|\\N-begin{array}{cc} x_1 & x_2 \N y_1 & y_2\N- \end{array} \N- Droite| + \N-Gauche|\N- Début{array}{cc} x_2 & x_3 \N- y_2 & y_3\N- fin{array} \Droit| + … + \left|\begin{array}{cc} x_{n-2} & x_{n-1} \\\N y_{n-2} & y_{n-1}\\\N \end{array} \N-right| + \N-ft|\N-begin{array}{cc} x_{n-1} & x_0 \\\N y_{n-1} & y_0\\\N \right| \right\}$

Où $x_n,y_n$ est un sommet de polygone exprimé en coordonnées cartésiennes, et $\left|\begin{array}{cc} x_0 & x_1 \\\\ y_0 & y_1\\\\\ \end{array} \right|$ fait référence à un déterminant, avec la valeur $x_0 \times y_1 – y_0 \times x_1$

Ne vous laissez pas décourager par l’exposé ci-dessus – utiliser cette méthode est plus facile que de comprendre ses fondements mathématiques. Lors de la recherche de cet article, j’ai trouvé un certain nombre de réponses à des questions d’étudiants qui étaient si complexes qu’elles ne pouvaient pas avoir éclairé l’étudiant. Dans cet article, je vais faire tout ce que je peux pour rendre cette méthode aussi simple et accessible que possible.

La méthode s’exprime le plus facilement sous forme d’algorithme :

• Les sommets d’un polygone irrégulier peuvent être représentés par des coordonnées cartésiennes : $x,y$.
• Chaque paire de coordonnées est traitée dans un algorithme de sommation de surface qui ressemble à ceci :
  

  $A = A + \frac{(x_1 \times y_0 – y_1 \times x_0)}{2}$
  $A = A + \frac{(x_2 \times y_1 – y_2 \times x_1)}{2}$
  …

• Une expression mathématique simple pour ce qui précède serait :
  

  (2) Surface d’un polygone irrégulier $\displaystyle A = \frac{1}{2} \sum_{i=m}^{n-1}{x_{i+1} \times y_i – y_{i+1} \times x_i}$

• NOTE : Dans l’équation (2), la figure traversée se termine avec le dernier élément de données fourni, elle ne répète pas l’élément initial comme indiqué dans l’équation (1) ci-dessus. Pour mes objectifs, expliqués ci-dessous, cette forme est intentionnelle – dans un levé de terrain, les données de terrain devraient fermer la figure, c’est-à-dire que le dernier élément devrait être égal au premier. Dans une telle application, fermer automatiquement la figure comme dans l’équation (1) dissimulerait des erreurs qui doivent être évaluées.

  Les utilisateurs peuvent préférer la forme montrée dans l’équation (1) ci-dessus, à des fins autres que la réduction des données d’arpentage. À ces fins, pendant le traitement, il suffit de réévaluer le premier élément de données à la fin de la traversée, ou de fournir des ensembles de données qui répètent le premier élément de données comme le dernier.

• Voici une fonction Python complète et fonctionnelle :
  

  def find_area(array) : a = 0 ox,oy = array for x,y in array : a += (x*oy-y*ox) ox,oy = x,y return a/2 

• L’argument « array » ci-dessus est un ensemble de coordonnées cartésiennes $x,y$, soit.e. ((10,10),(10,20),(20,20),(20,10),(10,10)). Remarquez à propos de cet ensemble de données que le premier élément de données est répété à la fin.

• Voici une fonction Python un peu plus complexe qui calcule à la fois l’aire et la longueur du périmètre :
  

  def find_area_perim(array) : a = 0 p = 0 ox,oy = array for x,y in array : a += (x*oy-y*ox) p += abs((x-ox)+(y-oy)*1j) ox,oy = x,y return a/2,p 

• Encore ce rappel : pour les deux exemples de code ci-dessus, dans des applications autres que la réduction de données de levés terrestres, l’ensemble de données fourni devrait inclure une copie du premier élément de données en tant que dernier, c’est-à-dire que la figure devrait être explicitement remplacée par un autre élément de données.c’est-à-dire que la figure devrait être explicitement fermée.

• J’ai choisi Python pour ces exemples parce qu’un listing Python maximise la signification algorithmique tout en minimisant le cruft.

• Les fonctions ci-dessus peuvent facilement être converties dans d’autres langages, presque directement – sauf la sommation de périmètre montrée ci-dessus, qui exploite le fait que Python supporte les nombres complexes. Pour les langages qui ne supportent pas les nombres complexes, on peut créer le résultat du périmètre de cette façon :

  C/C++ : p += sqrt(pow(x-ox,2)+pow(y-oy,2));

  Java : p += Math.sqrt(Math.pow(x-ox,2)+Math.pow(y-oy,2));

• Formellement, la longueur du périmètre est la somme des magnitudes des vecteurs :
  

  (3) Longueur du périmètre $\displaystyle P = \sum_{i=m}^{n-1}{\sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2}}$

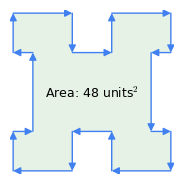
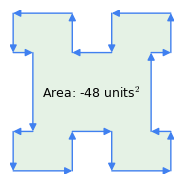Figure 1 : Vecteurs dans le sens des aiguilles d’une montre vs. vecteurs dans le sens inverse des aiguilles d’une montre

Voici quelques propriétés importantes de cette méthode :

• Le sommet d’origine choisi dans le polygone n’a aucune importance pour le calcul de l’aire ou du périmètre, il suffit que la figure soit fermée, c’est-à-dire que la dernière coordonnée soit égale à la dernière coordonnée.C’est-à-dire que la dernière coordonnée doit être égale à la première.
• « Règle du sens des aiguilles d’une montre » : l’ordre des vecteurs est significatif – si le périmètre est parcouru dans le sens des aiguilles d’une montre, le résultat de l’aire est positif, si c’est dans le sens inverse, il est négatif (figure 1). C’est cette propriété de la méthode qui permet de soustraire l’aire des inflexions d’une figure complexe comme dans la figure 1 – les « inflexions » représentent une traversée dans le sens inverse des aiguilles d’une montre à l’intérieur du polygone.
• De nombreuses applications de cette méthode utilisent des sources de données originales constituées de vecteurs polaires (un exemple est celui des descriptions légales d’arpentage), mais cette méthode nécessite des coordonnées cartésiennes. La conversion des coordonnées polaires en coordonnées cartésiennes est triviale, mais il est important de garder cette exigence à l’esprit.
• En outre, pour un calcul précis de la superficie, le polygone décrit doit être une figure fermée – la dernière coordonnée doit être égale à la première. Pour les applications utilisant des données de terrain constituées de vecteurs de longueur qui sont ensuite convertis en forme cartésienne, il est bon de comparer les coordonnées cartésiennes de début et de fin – elles doivent être égales. Par exemple, les anciens levés de terrain (avant l’ère de la puissance informatique bon marché) échouent régulièrement à ce test.

Cette section est un ordinateur d’aire/périmètre entièrement fonctionnel qui peut traiter des paires de données de coordonnées cartésiennes ou polaires entrées, ou des descriptions légales de levés. Il suffit de choisir un type de données (coordonnées cartésiennes x,y, coordonnées polaires m,θ ou une description légale d’arpentage) et de saisir (ou de coller) les données dans la zone de saisie ci-dessous. Vous pouvez également sélectionner des ensembles de données échantillons pour vous familiariser et vous entraîner.

Pour des raisons de sécurité du navigateur, pour éviter une saisie excessive et pour importer des quantités importantes de données d’une autre source, les lecteurs devront utiliser le presse-papiers de leur système. Il suffit de copier les données dans le presse-papiers de l’application source, puis de cliquer sur la zone de saisie des données en dessous et d’appuyer sur Crtl+A pour tout sélectionner, Ctrl+V pour coller les données d’ailleurs, et Ctrl+C pour copier vos propres données saisies. La plupart des navigateurs incluent également des fonctions de presse-papiers comme éléments de menu.

Choisissez le type de données :

cartésiennes (x,y)

polaires (m,θ)

Description du levé

Zone de saisie des données : Sélectionner tout : Ctrl+A | Copier : Ctrl+C | Coller : Ctrl+V

Zone de graphique:

Désolé – votre navigateur ne supporte pas la capacité graphique que cette fonctionnalité requiert –
considérez l’installation de Google Chrome ou Firefox.

Options:

Lignes

Flèches

Origine

Centre

Unité de longueur :

Largeur de ligne :

Inverse

Résultats:Sélectionner tout : Ctrl+A | Copier : Ctrl+C | Coller : Ctrl+V

Le calculateur d’aire/périmètre a trois modes d’entrée:

• Paires de coordonnées cartésiennes (x,y) :

  • Chaque coordonnée est une position bidimensionnelle avec une partie horizontale (x) et verticale (y) (une coordonnée cartésienne).
  • Les coordonnées ne sont pas cumulatives – chacune décrit indépendamment son emplacement.
  • Donc un carré serait :
    • 0,0 (origine)
    • 0,100 (haut)
    • 100,100 (droite)
    • 100,0 (bas)
    • 0,0 (retour à l’origine)
  

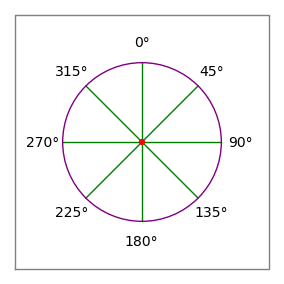  Figure 2 : Rose des vents

  • Les virgules dans l’exemple ci-dessus sont uniquement destinées à regrouper les paires de données pour le lecteur – elles n’ont aucune signification pour l’analyseur de données de l’ordinateur de la zone.
  • L’analyseur syntaxique est suffisamment robuste pour que l’exemple ci-dessus puisse être collé dans la zone de saisie des données de l’ordinateur et qu’il fonctionne (essayez-le).
  • La seule limitation est que les commentaires explicatifs ne peuvent pas contenir de chiffres.

• Paires de coordonnées polaires (m,θ) :

  • Chaque coordonnée est constituée d’une distance et d’un angle en degrés (un vecteur polaire).
  • Les angles suivent la convention de la boussole – 0 degré est vers le haut ou « nord », 90 degrés est vers la droite ou « est » (figure 2).
  • Contrairement à la forme cartésienne antérieure, ces coordonnées sont cumulatives – chaque nouveau vecteur s’ajoute à la position actuelle.
  • Donc un carré serait :
    • 100,0 (haut)
    • 100,90 (droite)
    • 100,180 (bas)
    • 100,270 (retour à l’origine)
  • Comme précédemment, cet exemple fonctionnera s’il est collé dans la zone de saisie de l’ordinateur et que le mode polaire est sélectionné.
  • Notez à propos des coordonnées polaires que l’origine est implicite et prédéfinie à x = 0, y = 0.
  

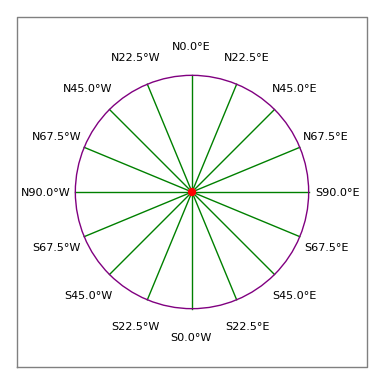  Figure 3 : Rose des vents de l’arpenteur

• Description légale :

  • D’abord, une explication de la relation entre la sélection « Unités de longueur » et l’affichage des résultats :
    • Pour chaque polygone, une liste de résultats de surface est calculée en utilisant un ensemble fixe d’unités de surface communes (pieds2, mètres2, etc.). Pour que cette liste d’aires soit significative, les unités de longueur d’entrée doivent être connues.
    • En mode cartésien et polaire, les entrées de données n’ont pas d’unités, donc l’utilisateur choisit les unités à attribuer aux longueurs. Ainsi, lorsque l’utilisateur change les unités de longueur, les valeurs de surface changent, les étiquettes de longueur changent, mais pas les valeurs de longueur.
    • En mode arpentage, la description légale contient des unités de longueur (pieds, mètres, etc.), ce qui signifie que les unités de longueur sont prédéfinies par la source. Donc, lorsque l’utilisateur change les unités de longueur, cela change les étiquettes et les valeurs de longueur, pas les valeurs de surface.
  • L’analyseur de description d’enquête est de loin le moins fiable des trois méthodes d’analyse des données – c’est plus une expérience qu’une méthode de conversion de données robuste.
  • J’ai écrit cet analyseur syntaxique en téléchargeant un certain nombre de descriptions légales (qui sont fournies à titre d’exemples dans le calculateur ci-dessus) et en réglant le code de l’analyseur syntaxique jusqu’à ce que toutes puissent être décodées avec succès.

  Les critères de « succès » étaient que le résultat ait la même surface carrée que celle revendiquée par la description, et que la figure se « ferme ».

  • Le terme « fermeture », et en particulier l’erreur de fermeture, est utilisé dans le travail d’arpentage pour décrire le degré auquel le point final de la traverse d’arpentage est égal au point initial. C’est rarement vrai dans la réalité – les erreurs de fermeture proviennent généralement d’erreurs dans le travail sur le terrain, et les levés plus anciens, publiés avant l’avènement de la puissance informatique bon marché, ont tendance à avoir des fermetures plutôt mauvaises ainsi que des estimations de la superficie carrée sauvagement inexactes.
  • Une description légale d’arpentage est une façon formelle de décrire une parcelle de terrain – sa forme et sa syntaxe ont surgi au fil des décennies par des conventions mutuellement acceptées, quelque peu arbitraires, partagées par les arpenteurs.
  • Pour cet ordinateur de surface/périmètre, les données saisies doivent suivre certaines conventions strictes auxquelles adhèrent certaines descriptions légales, mais pas toutes. Les éléments essentiels sont :
    • L’existence de l’expression « point de départ », qui sépare certains contenus préliminaires de ceux décrivant les dimensions de la parcelle décrite. Certains documents disent « True point of beginning », d’autres « Real point of beginning » et d’autres encore « Point of beginning ». Un analyseur syntaxique réussi doit supprimer le contenu qui précède cette phrase et conserver tout ce qui la suit.
    • Série de phrases qui décrivent un type particulier de vecteur polaire utilisé par les géomètres :
      • Le mot « Nord » ou « Sud », ou son abréviation « N » ou « S ».
      • Puis un angle exprimé en degrés, minutes et secondes.
      • Puis le mot « Est » ou « Ouest », ou son abréviation « E » ou « W ».
      • Puis une distance.
      • Puis une unité de distance – pieds, mètres, etc.
  • Voici quelques exemples différents de vecteurs d’arpenteur provenant de l’échantillon de descrtiptions légales :
    • N 2°0’0″ W – 63.50 pieds
    • N90°00’00 « W LE LONG D’UNE LIGNE PARALLÈLE À LADITE NORD D’UNE DISTANCE DE 6.00 PIEDS
    • Nord 0°06’O0″ Ouest une distance de 554.86 pieds
    • S. 22 degrés 41′ 55″ E. 174,10 pieds
  • Notez à propos des exemples ci-dessus qu’ils ont tous une syntaxe différente. Il existe de nombreuses descriptions légales que ce parseur ne réussira pas à décoder, uniquement parce que je n’ai pas essayé d’intégrer leur syntaxe. Mais il est important d’ajouter qu’un analyseur syntaxique vraiment robuste pour la multitude de descriptions légales existantes devrait être aussi intelligent que Watson.
  • Les utilisateurs de cet ordinateur de zone/périmètre peuvent vouloir éviter de soumettre des descriptions légales en texte brut et espérer que l’analyseur syntaxique trouvera la solution. Pour faire des entrées directes à la main (ou pour créer une liste de traverses ailleurs pour l’importation), utilisez cette convention :
    • Rappellez-vous qu’une entrée de traverse acceptable consiste en le mot « Nord » ou « Sud », ou la lettre « N » ou « S », suivi d’un maximum de trois nombres fournissant les degrés, minutes et secondes de l’angle, suivi du mot « Est » ou « Ouest » ou de la lettre « E » ou « W », suivi d’une distance, suivi d’une unité de distance.
    • Donc une entrée acceptable serait « N 30 15 45 W 100 pieds », signifiant une traversée de 100 pieds pointant à 30 degrés, 15 minutes et 45 secondes à l’ouest du Nord (c’est-à-dire environ 330 degrés de compas, voir la figure 3).
    • Les entrées des minutes et des secondes peuvent être sautées si elles sont égales à zéro, ou si l’entrée est en degrés décimaux, ou en degrés et minutes décimaux.
  • Il n’est pas difficile de convertir une description légale imprimée en de telles entrées, et il y a plusieurs façons de détecter les erreurs. Après que toutes les traverses ont été entrées, si la figure n’a pas d’erreur de fermeture et rapporte la même surface carrée que l’original, il y a des chances que les entrées soient correctes (ou qu’elles aient les mêmes erreurs que la description originale).
  • Après avoir entré une description légale de cette façon, s’il y a une erreur de fermeture inacceptable ou si la surface carrée est fausse, rappelez-vous que les données originales pourraient être fausses. Il existe un nombre indéterminé de descriptions légales qui n’ont jamais été vérifiées par une méthode informatique comme celle-ci et qui n’ont jamais été correctes.

En parcourant les exemples cartésiens (x,y), remarquez le rapport entre la surface et le périmètre des différentes formes. Le « polygone de forme bizarre » a un rapport intermédiaire, le cercle a le plus petit rapport, et l’espace de Hilbert a de loin le plus grand rapport. Cette relation s’étend aux dimensions supérieures, où l’on sait qu’une sphère a le plus grand volume par surface.

A propos de l’exemple du cercle – il s’agit d’un « cercle unitaire », un cercle dont le rayon est de un. Pour l’exemple fourni, l’aire est approximativement de $\pi$ et le périmètre approximativement de $2\pi$, les bonnes valeurs pour un cercle unitaire. Pour que ces valeurs soient plus que des approximations, pour qu’elles soient exactement égales $\pi$ et $2\pi$, il faudrait que le nombre de côtés du polygone soit infini. J’ai décidé de ne pas le faire. 🙂

L’exemple de l’espace de Hilbert a été généré à l’aide d’un algorithme Sage avec un choix d’ordre modeste (pour éviter de générer trop de données). En principe, un espace de Hilbert peut avoir un rapport infini entre le périmètre et la surface en deux dimensions, ou entre la surface et le volume en trois dimensions. Pour voir à quel point un espace de Hilbert peut devenir complexe, cliquez ici pour voir un espace de Hilbert d’ordre 7.

Notez à propos de l’exemple de Hilbert que l’aire calculée est proche de 1/2 pour une surface 1×1. Idéalement, sans la nécessité de convertir une figure de ligne en une figure d’aire et avec le bon algorithme, l’aire de la surface serait exactement la moitié de celle d’un carré de mêmes dimensions.

Le mode d’entrée polaire est plus ou moins égal au graphisme de la tortue, si l’on substitue zéro degré à « haut », 90 degrés à « droite », etc. et si chaque séquence de rotation et de déplacement est regroupée en une seule commande. L’utilisation du mode de saisie polaire est un moyen facile de construire à la main une forme complexe, parce que les distances et les angles sont plus faciles à suivre que les coordonnées cartésiennes.

J’ai utilisé pour la première fois la méthode de calcul de la zone d’arpentage décrite ci-dessus il y a des années lorsque je vivais dans l’Oregon rural, entouré de personnes qui avaient besoin de connaître la superficie et le périmètre de leurs propriétés. J’ai rencontré de nombreux exemples choquants où les agents immobiliers trompaient effrontément les gens qui n’avaient aucun moyen de savoir ce qui se passait. À plusieurs reprises, j’ai calculé une superficie à partir d’une description légale, pour découvrir que la revendication de l’acte de garantie concernant la superficie était très inexacte – et toujours supérieure à la réalité.

À une occasion, on m’a demandé de diviser une propriété en deux sections égales et de créer des descriptions légales pour chacune. Parce que j’avais un Apple II nouvellement acquis (qui avait la puissance de traitement d’un taille-crayon moderne), cela a été très facile – mais en travaillant, j’ai réalisé que la superficie totale était erronée d’environ trois acres, soit environ 25% du total. J’ai confronté la compagnie de titre, qui a répondu effrontément, « Vous voyez ici, où l’acte dit « plus ou moins » ? »

A une autre occasion, j’ai commencé un achat de terrain, mais prévenu par l’expérience ci-dessus, lorsque j’ai reçu la police de titre, j’ai décidé d’entrer sa description légale dans mon programme pour voir si la revendication de la superficie était exacte. Mais à mon grand désarroi, j’ai découvert que toutes les polices de titre pour les parcelles de cette section avaient la même description légale – celle de la première propriété arpentée. Il s’avère que la société de développement foncier a décidé d’économiser de l’argent en arpentant un seul des dizaines de lots proposés à la vente, et d’inclure cette description légale dans toutes les polices de titre. Ils étaient sûrs de s’en sortir – après tout, qui s’y connaît en mathématiques ?

Après avoir discuté avec la société de titres et le promoteur, en essayant de les persuader de payer pour des levés afin que les descriptions légales ne soient pas des fictions polies, j’ai abandonné et décidé de ne pas acheter le terrain. C’était comme découvrir comment la saucisse est faite – il est possible d’en savoir trop.

• 04.15.2013 Version 1.3. Ajout d’une explication détaillée du format de données par défaut, c’est-à-dire des listes qui répètent le premier point de données comme le dernier.
• 03.24.2013 Version 1.2. Optimisation plus poussée de l’analyseur syntaxique de description d’enquête, ajout de plus de champs de données de résultat.
• 03.23.2013 Version 1.1. Amélioration de l’analyseur syntaxique de description légale pour traiter plus de types de descriptions, ajout d’un sélecteur d’unités de longueur et d’une liste de résultats des zones en unités communes.
• 03.22.2013 Version 1.0. Version publique initiale.