Événements dépendants vs indépendants
Il y a quelques posts, j’ai commencé à parler des probabilités. Je veux passer un peu plus de temps sur le sujet parce que c’est l’un de ces concepts qui peuvent être évidemment faciles une minute et carrément déroutants la minute suivante.
Chaque fois que vous abordez un problème de probabilité impliquant plus d’un événement, commencez par vous demander si les événements sont dépendants ou indépendants, c’est-à-dire si un événement modifie la probabilité de l’autre événement ? Est-ce que le premier événement qui se produit change le système ?
(Tirer plusieurs cartes d’un jeu sans remplacement est un exemple classique d’un événement dépendant. Lorsque nous tirons la première carte, le système passe de 52 options possibles à 51 avant que le deuxième événement ne se produise.)
Dans la vie réelle, les humains ont tendance à confondre la dépendance tout le temps. Par exemple, vous tirez à pile ou face une pièce de monnaie équitable. Elle tombe face 10 fois de suite. Vous êtes certain que le prochain lancer sera forcément pile… n’est-ce pas ?
Quelles sont les chances que le prochain lancer soit à nouveau pile ?
C’est toujours 1/2. Tirer à pile ou face est un événement indépendant. En d’autres termes, le résultat du prochain pile ou face n’est pas influencé par ce qui s’est passé précédemment. C’est comme si c’était la première fois que vous jouiez à pile ou face. La probabilité n’est pas modifiée.
Pourquoi a-t-on « l’impression » que ce devrait être pile alors ?
Nous avons tendance à penser aux événements ensemble, plutôt qu’individuellement. Bien que la probabilité de lancer face reste la même pour chaque lancer, la chance combinée de lancer 11 faces à la suite est faible.
Calculons-la.
Nous avons appris dans la leçon de probabilité précédente que lorsque nous enchaînons plusieurs événements et que nous voulons qu’ils se produisent tous (le scénario « et »), nous devons multiplier leurs probabilités ensemble.
Puisque chaque lancer de pièce de monnaie a une probabilité de face égale à 1/2, j’ai simplement besoin de multiplier ensemble 1/2 onze fois.
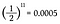
C’est une chance de 0,05% de lancer onze têtes à la suite ! Mais avant que vous n’exhaliez un soupir de soulagement et que vous ne disiez : « Vous voyez, je le savais ! », calculons la probabilité d’obtenir une queue à la place lors du onzième lancer.
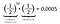
Oui, c’est exact. Il est tout aussi probable de faire tomber dix têtes suivies d’une queue que de faire tomber onze têtes d’affilée. En fait, comme la probabilité individuelle de tomber sur pile est la même que celle de tomber sur face, chaque arrangement de 11 tirages de pièces de monnaie donnera lieu à la même probabilité de 0,0005. Chaque disposition a la même probabilité.
Alors… pourquoi est-il « SENTIMENT » improbable de tirer dix fois sur la tête à la suite ??
Cette idée fausse courante n’est pas due à la probabilité, mais à une mauvaise compréhension de la combinatoire et des permutations.
Jusqu’ici, nous avons établi que :
- La probabilité de tirer sur la tête ou sur la queue est la même pour chaque lancer individuel : P(H) = P(T) = 1/2.
- Chaque arrangement unique (permutation) des lancers de pièces de monnaie possibles est également probable.
Alors qu’est-ce qui se passe ?
Comprendre l’espace d’échantillonnage
L’espace d’échantillonnage est simplement une liste de tous les arrangements (permutations) de résultats possibles. Comme l’espace d’échantillonnage pour 11 tirages consécutifs à pile ou face est plutôt grand, examinons plutôt un cas plus simple.
L’espace d’échantillonnage pour quatre tirages à pile ou face est :

Intuitivement, on pourrait penser : il est plus probable de tirer 2 têtes et 2 queues sur quatre tirages que toutes les têtes ou toutes les queues.
Et c’est vrai. Faisons le calcul.
Nous savons que chacune des seize permutations a la même probabilité car P(H) = P(T) = 1/2. Donc, chaque permutation a une probabilité égale de :

Note : Comme l’espace d’échantillonnage représente toutes les issues possibles, la somme de toutes les probabilités est toujours égale à 1 (Par exemple, 0,0625 – 16 = 1).
En regardant notre espace d’échantillonnage, combien de permutations différentes du lancer de la pièce de monnaie aboutissent à n’importe quelle combinaison 0de 2 têtes et 2 queues ?

Notez que 6 des 16 résultats possibles aboutissent à une combinaison deux têtes/deux queues. Comme n’importe laquelle de ces six permutations répond à nos critères, on considère qu’il s’agit d’un scénario » ou » – il faut donc additionner les probabilités (ou simplement les multiplier par 6 puisqu’elles sont toutes identiques).
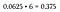
C’est une chance de 37,5% de lancer une combinaison de 2 têtes et 2 queues, ce qui est bien plus grand que la probabilité de lancer toutes les têtes ou toutes les queues (qui reste de 6.25% chacune puisqu’il n’y a qu’une seule permutation de chacune dans notre espace d’échantillonnage).
C’est pourquoi nous savons intuitivement qu’il est plus probable de lancer un nombre égal de têtes et de queues, que de lancer toutes les sortes, tout en maintenant le fait que les événements sont indépendants avec des lancers individuels et des permutations également susceptibles de se produire.
Permutations &Combinaisons
Une grande partie du calcul réussi des probabilités consiste à comprendre les permutations et les combinaisons de manière approfondie. C’est donc là que nous nous dirigeons maintenant!