Függő vs. független események
Pár hozzászólással ezelőtt elkezdtem beszélni a valószínűségekről. Szeretnék még egy kis időt szánni a témára, mert ez egyike azoknak a fogalmaknak, amelyek az egyik percben nyilvánvalóan egyszerűek, a másikban pedig egyenesen zavarosak lehetnek.
Amikor egynél több eseményt tartalmazó valószínűségi problémához közelítünk, kezdjük azzal a kérdéssel, hogy az események függőek vagy függetlenek-e, azaz az egyik esemény megváltoztatja-e a másik esemény valószínűségét? Az első esemény bekövetkezése megváltoztatja-e a rendszert?
(A több lap csere nélküli húzása egy pakliból klasszikus példája a függő eseménynek. Amikor kihúzzuk az első kártyát, a rendszer 52 lehetséges lehetőségről 51-re változik, mielőtt a második esemény bekövetkezik.)
A való életben az emberek hajlamosak állandóan összekeverni a függőséget. Például feldobunk egy tisztességes érmét. Tízszer egymás után fejre esik. Biztos vagy benne, hogy a következő dobás biztosan írás lesz…igaz?
Mi az esélye annak, hogy a következő érme ismét fej lesz?
Még mindig 1/2. Az érme feldobása egy független esemény. Más szóval a következő feldobás kimenetelét nem befolyásolja, hogy mi történt korábban. Olyan, mintha most dobnád fel először az érmét. A valószínűség változatlan.
Miért “érezzük” úgy, hogy akkor írnak kellene lennie?
Hajlamosak vagyunk együtt gondolkodni az eseményekről, nem pedig külön-külön. Bár a fej dobás valószínűsége minden dobásnál ugyanaz marad, a 11 egymás utáni fej dobás együttes esélye kicsi.
Kalkuláljuk ki.
Az előző valószínűségi leckében megtanultuk, hogy amikor több eseményt fűzünk egymáshoz, és azt akarjuk, hogy mind bekövetkezzen (az “és” forgatókönyv), akkor a valószínűségeiket össze kell szoroznunk.
Mivel minden egyes pénzfeldobásnál a fej valószínűsége 1/2, egyszerűen tizenegyszer kell összeszoroznom az 1/2-t.
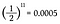
Ez 0,05% esélye annak, hogy tizenegy fejet dobunk egymás után! De mielőtt megkönnyebbülten felsóhajtanál, és azt mondanád: “Látod, tudtam!”, számoljuk ki, mekkora az esélye annak, hogy a tizenegyedik dobásnál inkább farok lesz.
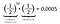
Igen, így van. Ugyanolyan valószínűséggel dobunk tíz fejet, amelyet egy farok követ, mint tizenegy fejet egymás után. Valójában, mivel a fej feldobásának egyedi valószínűsége megegyezik az írás feldobásának valószínűségével, a 11 pénzfeldobás minden egyes elrendezése ugyanolyan valószínűséggel 0,0005-öt eredményez. Minden elrendezés egyforma valószínűségű.
Szóval… miért “ÉRZEM” valószínűtlennek tíz fejet dobni egymás után?”
Az általános tévhit nem a valószínűségszámítás, hanem a kombinatorika és a permutációk félreértése miatt van.
Ezidáig megállapítottuk, hogy:
- A fej vagy írás dobásának valószínűsége minden egyes dobásnál egyforma valószínűségű: P(H) = P(T) = 1/2.
- A lehetséges pénzfeldobások minden egyedi elrendezése (permutációja) egyforma valószínűségű.
Mit ad tehát?
A mintatér megértése
A mintatér egyszerűen az összes lehetséges kimenetelű elrendezés (permutáció) felsorolása. Mivel a mintatér 11 egymást követő pénzfeldobás esetén meglehetősen nagy, vizsgáljunk meg helyette egy egyszerűbb esetet.
A négy pénzfeldobásra vonatkozó mintatér:

Intuitívan azt gondolhatjuk: valószínűbb, hogy négy dobásból 2 fejet és 2 írást dobunk, mint hogy csak fejet vagy csak írást.
És ez igaz is. Végezzük el a matematikát.
Tudjuk, hogy a tizenhat permutáció mindegyike egyforma valószínűségű, mert P(H) = P(T) = 1/2. Tehát minden permutációnak egyenlő a valószínűsége:

Megjegyezzük: Mivel a mintatér az összes lehetséges kimenetet képviseli, a valószínűségek összege mindig 1 (Pl. 0,0625 – 16 = 1).
A mintaterünket tekintve hány különböző érmefeldobási permutáció eredményez bármilyen 0f 2 fej és 2 írás kombinációt?

Megjegyezzük, hogy a 16 lehetséges kimenetelből 6 eredményez két fej/két írás kombinációt. Mivel e hat permutáció közül bármelyik megfelel a kritériumainknak, ez egy “vagy” forgatókönyvnek tekinthető – tehát adjuk össze a valószínűségeket (vagy egyszerűen szorozzuk meg 6-mal, mivel mindegyik ugyanaz).
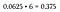
Ez 37,5%-os esélyt jelent a két fej és két írás kombináció dobására, ami jóval nagyobb, mint az összes fej vagy az összes írás dobásának valószínűsége (ami 6 marad.25%, mivel a mintatérben csak egy-egy permutáció létezik).
Ez az oka annak, hogy intuitív módon tudjuk, hogy nagyobb a valószínűsége annak, hogy egyenlő számú fejet és írásjelet dobunk, mint annak, hogy az összeset egyféleképpen dobjuk, miközben továbbra is fennmarad az a tény, hogy az események függetlenek, az egyes dobások és permutációk egyforma valószínűséggel fordulnak elő.
Permutációk &Kombinációk
A valószínűségek sikeres kiszámításának nagy része a permutációk és kombinációk alapos megértése. Tehát ez az, ahová a következőkben tartunk!