A természetben körülnézve talán észrevettél már olyan bonyolult növényeket, mint ezek:


Ez a páfrányfenyő sok kis levélből áll, amelyek egy nagyobb levélből ágaznak ki.


Ez a Romanesco brokkoli kisebb kúpos gömbökből áll, amelyek egy nagyobb körül spirálisan tekerednek.
Elsőre ezek rendkívül összetett formáknak tűnnek – de ha jobban megnézzük, észrevehetjük, hogy mindkettő viszonylag egyszerű mintát követ: az egyes részek pontosan ugyanúgy néznek ki, mint az egész növény, csak kisebbek. Ugyanaz a minta ismétlődik újra és újra, kisebb léptékben.
A matematikában ezt a tulajdonságot önhasonlóságnak nevezzük, és az ezzel rendelkező alakzatokat fraktáloknak nevezzük. Ezek az egész matematika legszebb és legbizarrabb objektumai közé tartoznak.
A saját fraktáljaink létrehozásához egy egyszerű mintával kell kezdenünk, majd azt újra és újra megismételni, kisebb léptékben.
A legegyszerűbb minták egyike lehet egy vonalszakasz, amelynek egyik végéből két további szakasz ágazik ki. Ha megismételjük ezt a mintát, akkor mindkét kék szegmensnek a végén szintén két további elágazás lesz.
A kék pontokat mozgatva megváltoztathatjuk az összes elágazás hosszát és szögét. Ezután a lenti csúszkával növelhetjük az ismétlések számát.
Az ágak helyzetétől függően teljesen különböző mintákat hozhatunk létre – a fenti páfrányhoz, egy fához vagy egymásba ágyazott ötszögekhez hasonlót. Mi mást találhatsz még?
Egy másik híres fraktál a Sierpinski-háromszög. Ebben az esetben egy nagy, egyenlő oldalú háromszögből indulunk ki, majd a megmaradt részekből többször kisebb háromszögeket vágunk ki.
Figyeljük meg, hogy a végső alakzat három azonos másolatából áll, és ezek mindegyike a teljes háromszög még kisebb másolataiból áll! A háromszöget a végtelenségig zoomolhatnánk, és a minták és alakzatok mindig ismétlődni fognak.
A fejezet elején látható növények éppen úgy néznek ki, mint a fraktálok, de nyilvánvalóan lehetetlen valódi fraktálokat létrehozni a való életben. Ha ugyanazt a mintát ismételgetnénk újra és újra, egyre kisebbre és kisebbre, akkor végül olyan sejtekhez, molekulákhoz vagy atomokhoz jutnánk, amelyek már nem oszthatók.
A matematika segítségével azonban elgondolkodhatunk azokon a tulajdonságokon, amelyekkel a valódi fraktálok “rendelkeznének” – és ezek nagyon meglepőek…
Fraktál dimenziók
Először is gondoljunk a fraktálok dimenziójára. Egy vonalnak van dimenziója . Ha 2-szeresére méretezzük, akkor a hossza 21=2-szeresére nő. Nyilvánvaló!
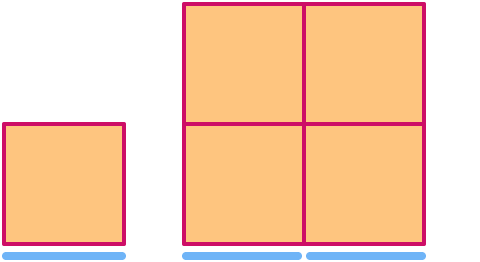
Egy négyzet dimenziója . Ha 2-szeresére méretezzük, akkor a területe 22= .22-szeresére nő
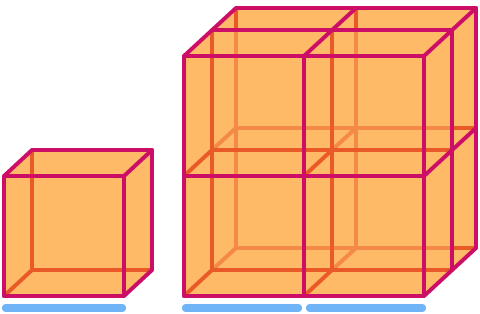
Egy kocka mérete . Ha 2-szeresére méretezzük, akkor a térfogata 23-szorosára nő= . Vegyük észre, hogy a képen látható nagyobb kocka a kisebb kocka 8 példányából áll!
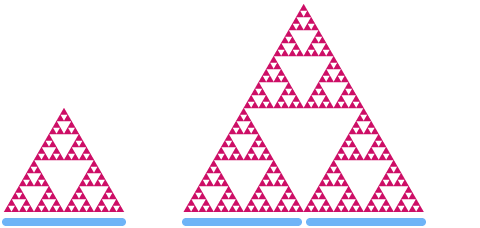
Most nézzük meg a Sierpinski-háromszöget. Ha 2-szeresére méretezzük, akkor láthatjuk, hogy a “területe” .
Mondjuk, hogy d a Sierpinski-háromszög dimenziója. A fenti mintát alkalmazva 2d=3-at kapunk. Más szóval d = log23log32 ≈ 1,585…
De várjunk csak … hogyan lehet valaminek olyan dimenziója, ami nem egész szám? Lehetetlennek tűnik, de ez csak a fraktálok egyik furcsa tulajdonsága. Valójában ez adja a fraktálok nevét: tört dimenzióval rendelkeznek.
Minden egyes iterációval eltávolítjuk a Sierpinski-háromszög területének egy részét. Ha ezt végtelen sokszor megtehetnénk, valójában nem maradna terület: ezért a Sierpinski-háromszög valami a kétdimenziós terület és az egydimenziós vonal között.
Míg sok fraktál önhasonló, egy jobb definíció szerint a fraktálok olyan alakzatok, amelyek nem egész számú dimenzióval rendelkeznek.
A Koch-hópehely
A természetben sok olyan alakzat van, amely fraktálnak tűnik. A fejezet elején már láttunk néhány növényt. További nagyszerű példák a hópelyhek és a jégkristályok:
A saját fraktál hópehelyünk létrehozásához ismét egy olyan egyszerű eljárást kell találnunk, amelyet újra és újra alkalmazhatunk.
A Sierpinski-háromszöghöz hasonlóan kezdjük egyetlen, egyenlő oldalú háromszöggel. Azonban ahelyett, hogy minden lépésnél kisebb háromszögeket távolítanánk el, inkább kisebb háromszögeket adunk hozzá az éle mentén. Minden háromszög oldalhossza 131412 az előző lépésben lévő háromszögek közül.
Az így kapott alakzatot Koch-hópehelynek nevezik, Helge von Koch svéd matematikusról elnevezve. Vegyük észre még egyszer, hogy a hópehely élének kis szakaszai pontosan ugyanúgy néznek ki, mint a nagyobb szakaszok.
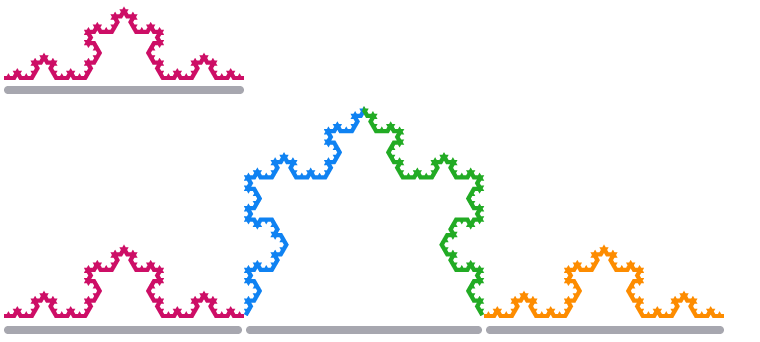
Ha a Koch-hópehely egy élszegmensét háromszorosára méretezzük, a hossza megnégyszereződik.
A méretek és a méretaránytényezők közötti fenti összefüggést felhasználva a 3d=42d=42d=34d=3 egyenletet kapjuk. Ez azt jelenti, hogy a Koch-hópehely mérete d=log34≈1,262.
Felület
A Koch-hópelyhek létrehozása majdnem olyan, mint egy rekurzív sorozat: ismerjük a kiindulási alakzatot (egy háromszög), és tudjuk, hogyan jutunk el egyik tagból a másikba (minden élre újabb háromszögek hozzáadásával):


új háromszögek

új háromszögek

új háromszögek
Az első iteráció után a hozzáadott új háromszögek száma minden lépésnél aszeresére nő. Ugyanakkor ezeknek az új háromszögeknek a területe minden egyes lépésben egy szorzóval csökken.
Tegyük fel, hogy az első háromszög területe 1. Ekkor a következő három három háromszög összes területe 3×19=13 lesz. A következő lépések mindegyike geometriai sorozatotaritmetikai sorozatkvadratikus sorozatot alkot, amelynek közös hányadosa 499443.
A végtelen geometriai sorok összegére vonatkozó képlet segítségével kiszámíthatjuk, hogy a Koch-hópehely teljes területe
A=1+13×11-491+949-14=85=1.6.
kerülete
Megpróbálhatjuk kiszámítani a Koch-hópehely kerületét is. Mint már korábban láttuk, a kerület hossza minden lépésnél 433414-szeresére változik.
Ez azt jelenti, hogy ismét egy geometriai sorozatunk van – de ebben az esetben nem konvergálkonvertál 0-ra nincs első tagja. Ez azt jelenti, hogy a Koch-hópehely kerülete valójában végtelen hosszú!

Ha ez ellentmondásosnak tűnik, ne feledjük, hogy minden lépésnél megszorozzuk a kerületet 43-mal, és ezt végtelen sokszor tesszük.
Majdnem elképzelhetetlen, hogy egy alakzat véges területtel és egyben végtelen kerülettel is rendelkezzen – de ez csak egy a fraktálok számos váratlan tulajdonsága közül.
El tudsz találni más módot arra, hogy saját fraktálokat hozz létre?
“A lelkem körös-körül fagyott fraktálokon spirálozik…”
Menger Spongya
A fraktáloknak nem kell “laposnak” lenniük, mint a fenti példák közül soknak. Az egyik leghíresebb háromdimenziósnak tűnő fraktál a Menger-szivacs, amelyet Karl Menger matematikusról neveztek el, aki 1926-ban írta le először.
Egy tömör kockából indulunk ki, és ismételten egyre kisebb és kisebb lyukakat fúrunk az oldalaiba. A lyukak minden újabb iterációja 131214 lyukszélességű, mint az előző iteráció.
Egy 3×3×3 kocka 27 kisebb kockából áll, de itt ezek közül néhányat eltávolítottunk. A Menger-szivacs önmagának 3-szor kisebb másolataiból áll.
Most megpróbálhatjuk kiszámítani a Menger-szivacs d dimenzióját, ugyanúgy, ahogy a fenti Koch-hópehelynél tettük. Ebben az esetben 3d=20, vagy d=log320≈2,727.
Ha elképzeljük, hogy egyre több és több lyukat vágunk ki, végtelen sokszor, akkor nem maradna tényleges térfogat. Ezért “nem egészen” háromdimenziós a kocka!
Fraktál partvonalak
Az eddig látott fraktálok egyik legfontosabb jellemzője, hogy a végtelenségig “ráközelíthetünk”, és mindig új mintákat találunk. Lewis Fry Richardson brit matematikus 1920 körül rájött, hogy ugyanez igaz számos ország határára vagy partvonalára is.
Az ország alapformájával kezdjük, és ahogy ráközelítünk, hozzáadjuk a folyóvölgyeket, öblöket és torkolatokat, majd az egyes sziklákat, sziklákat, kavicsokat és így tovább:
Ez jelentős problémát jelent, amikor egy ország határának hosszát próbáljuk kiszámítani – hogyan döntsük el, hogy meddig nagyítsunk be, és milyen zugokat és rögöket vegyünk figyelembe?
Az egyik módszer, amivel megmérhetjük például Nagy-Britannia partvonalának hosszát, hogy fogunk egy hosszú vonalzót, végigjárjuk a partokat, majd összeadjuk a távolságokat.
Ha a vonalzó ${vonalzó}km hosszú, akkor ${count}-szer kell használnunk, így a teljes partvonal ${count} lesz. × ${vonalzó} = ${szám * vonalzó}km.
Folytathatjuk a sort, egyre kisebb és kisebb vonalzóval, és minden alkalommal egy kicsit hosszabb lesz a partvonal hosszára vonatkozó eredményünk. Akárcsak korábban a Koch-hópehelynél, úgy tűnik, hogy Nagy-Britannia partvonala végtelenül hosszú! Ezt gyakran nevezik partvonal-paradoxonnak.
Néhány évtizeddel később Benoit Mandelbrot matematikus az IBM-nél dolgozva Richardson munkájára bukkant egy kidobott könyvtári könyvben. Felismerte jelentőségét, és azt is, hogyan kapcsolódik a fraktálokkal és dimenziókkal kapcsolatos újabb kutatásokhoz.
A brit partvonal kétségtelenül fraktálnak “látszik”, de nem önhasonló, mint más, korábban látott fraktálok. Ahhoz, hogy megtaláljuk a méretét, felrajzolhatjuk egy rácsra, és megszámolhatjuk, hány cellával metszi magát.
Kezdetben 88 metsző cellája van. Ha a partvonalat 2-szeresére méretezzük, akkor 197 egymást metsző cella lesz – több mint kétszer annyi!
A partvonal mérete 19788-szorosára nőtt. Mint korábban, ez azt jelenti, hogy a partvonal dimenziója
d=log219788≈1,16
Ha ezt megismételnénk nagyobb rácshálóval, azt találnánk, hogy Nagy-Britannia partvonalának dimenziója valójában körülbelül 1,21. Mandelbrot rájött, hogy ez a fraktáldimenzió egyben egy alakzat érdességének a mértéke is – ez egy új fogalom, amelyre fontos alkalmazásokat talált a matematika és a tudomány számos más területén.
Még több fraktál a természetben és a technológiában
Míg a valódi fraktálok soha nem jelenhetnek meg a természetben, sok olyan tárgy van, amely szinte fraktálnak tűnik. Láttunk már növényeket, hópelyheket és partvonalakat, és itt van még néhány példa:
Hegylánc Közép-Ázsiában
Gangesz folyó deltája Indiában
Villámok
Villámok
Vérerek a retinában
Grand Canyon az USA-ban
Felhők
Mindezek az objektumok teljesen véletlenszerűnek tűnhetnek, de a fraktálokhoz hasonlóan van egy mögöttes minta, amely meghatározza a kialakulásukat. A matematika segíthet jobban megérteni az alakzatokat, és a fraktáloknak olyan területeken vannak alkalmazásai, mint az orvostudomány, a biológia, a geológia és a meteorológia.
Számítógépen generált fraktál terep
A fraktálokat a természet valósághű “másolatainak” létrehozására is használhatjuk, például videojátékokban vagy számítógépes filmekben használt tájképek és textúrák formájában. A képen látható vizet, hegyeket és felhőket teljes egészében számítógép készítette, fraktálok segítségével!
És még meg is fordíthatjuk ezt a folyamatot a digitális képek tömörítéséhez, a fájlméretük csökkentése érdekében. Az első algoritmusokat Michael Barnsley és Alan Sloan fejlesztette ki az 1980-as években, és még ma is kutatják az újakat.