Equazioni di SHM
Consideriamo un blocco attaccato a una molla su un tavolo senza attrito (Figura \(\PageIndex{3}). La posizione di equilibrio (la posizione in cui la molla non è né tesa né compressa) è segnata come x = 0 . Nella posizione di equilibrio, la forza netta è zero.
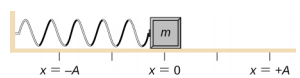
Si lavora sul blocco per tirarlo fuori fino alla posizione di x = + A, e poi lo si rilascia da fermo. La posizione massima di x (A) è chiamata ampiezza del movimento. Il blocco inizia ad oscillare in SHM tra x = + A e x = -A, dove A è l’ampiezza del moto e T è il periodo dell’oscillazione. Il periodo è il tempo di un’oscillazione. La figura \(\PageIndex{4}) mostra il movimento del blocco mentre completa un’oscillazione e mezza dopo il rilascio.
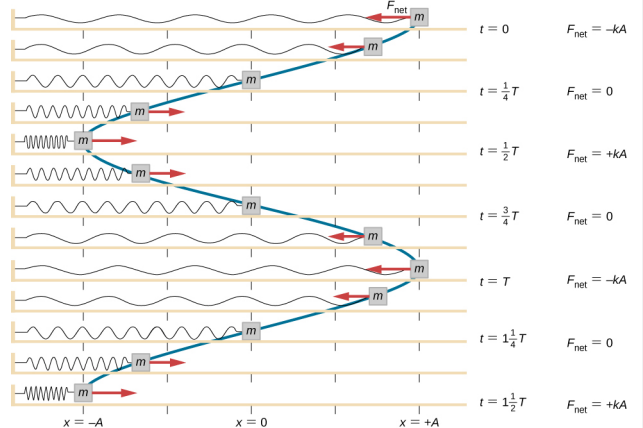
\
L’equazione per la posizione in funzione del tempo \(x(t) = A\cos( \omega t)\) è buona per modellare i dati, dove la posizione del blocco al tempo iniziale t = 0.00 s è all’ampiezza A e la velocità iniziale è zero. Spesso quando si prendono dati sperimentali, la posizione della massa al tempo iniziale t = 0,00 s non è uguale all’ampiezza e la velocità iniziale non è zero. Consideriamo 10 secondi di dati raccolti da uno studente in laboratorio, mostrati nella Figura \(\PageIndex{6}\).
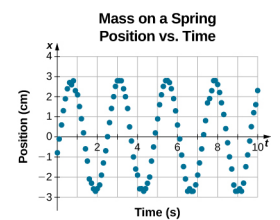
I dati nella Figura \(\PageIndex{6}\) possono ancora essere modellati con una funzione periodica, come una funzione coseno, ma la funzione è spostata a destra. Questo spostamento è noto come uno spostamento di fase ed è solitamente rappresentato dalla lettera greca phi (\(\phi\)). L’equazione della posizione in funzione del tempo per un blocco su una molla diventa
Questa è l’equazione generalizzata per SHM dove t è il tempo misurato in secondi, \(\omega\) è la frequenza angolare con unità di secondi inversi, A è l’ampiezza misurata in metri o centimetri, e \(\phi\) è lo spostamento di fase misurato in radianti (Figura \(\PageIndex{7}). Va notato che poiché le funzioni seno e coseno differiscono solo per uno spostamento di fase, questo movimento potrebbe essere modellato usando sia la funzione coseno che quella seno.
La velocità della massa su una molla, oscillante in SHM, può essere trovata prendendo la derivata dell’equazione di posizione:
Perché la funzione seno oscilla tra -1 e +1, la velocità massima è l’ampiezza per la frequenza angolare, vmax = A\(\omega\). La velocità massima si verifica nella posizione di equilibrio (x = 0) quando la massa si muove verso x = + A. La velocità massima in direzione negativa è raggiunta nella posizione di equilibrio (x = 0) quando la massa si muove verso x = -A ed è uguale a -vmax.
L’accelerazione della massa sulla molla può essere trovata prendendo la derivata temporale della velocità: