Area di un poligono irregolare

Questo articolo descrive una semplice soluzione ad un problema geometrico, uno che trovo descritto in modi troppo complessi online. Il problema è calcolare l’area e la lunghezza del perimetro di una figura bidimensionale chiusa come la pianta di una stanza, o un terreno, o qualsiasi altra figura bidimensionale delimitata (un “poligono irregolare”), indipendentemente da quanto sia complesso.

Non pretendo certo l’originalità di questo metodo. Versioni esistono fin dai tempi di Gauss o prima. Ma la maggior parte degli articoli online descrivono il metodo in modi inutilmente complessi. I riferimenti includono l’articolo di Wikipedia Shoelace Formula, un metodo altrettanto complesso nell’articolo Polygon, e una serie di articoli che sembrano calcolati più per dimostrare l’erudizione dell’autore che per fornire l’incarnazione meno complessa del metodo. Questo articolo (PDF) mostra una delle espressioni meno complesse (ma per nulla semplice):

(1) $A = \frac{1}{2} x_0 & x_1 & y_0 & y_1\\ \frazione \fine \fine \frazione \fine \fine \fine \fine \fine \fine \fine \fine \fine \fine \fine \fine \fine \fine \x_1 & x_2 & y_1 & y_2> fine x_2 & x_3 & y_2 & y_3 \fine \fine \fine \fine \fine \fine \fine \fine \fine \fine \fine \fine \fine \fine \fine \fine \fine \fine \fine \destra| + … + x_{n-2} & x_{n-1} & y_{n-2} & y_{n-1} & y_{n-1} & fine \x_{n-1} & x_0 \4560> y_{n-1} & y_0} \4560> fine \dove $x_n,y_n$ è un vertice del poligono espresso in coordinate cartesiane, e $left|begin{array}{cc} x_0 & x_1 \\ y_0 & y_1\ \end{array} \destra|$ si riferisce ad un determinante, con il valore $x_0 \volte y_1 – y_0 \volte x_1$

Non siate scoraggiati dalla precedente esposizione – usare questo metodo è più facile che capirne le basi matematiche. Durante la ricerca di questo articolo ho trovato un certo numero di risposte a domande di studenti che erano così complesse che non avrebbero potuto illuminare lo studente. In questo articolo farò tutto il possibile per rendere questo metodo il più semplice e accessibile possibile.

Il metodo è espresso più facilmente come un algoritmo:

• I vertici di un poligono irregolare possono essere rappresentati come coordinate cartesiane: $x,y$.
• Ogni coppia di coordinate viene elaborata in un algoritmo di somma di aree che assomiglia a questo:
  

  $A = A + \frac{(x_1 \tempo y_0 – y_1 \tempo x_0)}{2}$
  $A = A + \frac{(x_2 \tempo y_1 – y_2 \tempo x_1)}{2}$
  …

• Una semplice espressione matematica per quanto sopra sarebbe:
  

  (2) Area del poligono irregolare $displaystyle A = \frac{1}{2} \sum_{i=m}^{n-1}{x_{i+1} \tempo y_i – y_{i+1} \tempi x_i}$

• NOTA: Nell’equazione (2), la figura attraversata finisce con l’ultimo dato fornito, non ripete l’elemento iniziale come mostrato nell’equazione (1) sopra. Per i miei scopi, spiegati più avanti, questa forma è intenzionale – in un rilevamento del terreno i dati del campo dovrebbero chiudere la figura, cioè l’elemento finale dovrebbe essere uguale al primo. In una tale applicazione, chiudere automaticamente la figura come nell’equazione (1) nasconderebbe errori che devono essere valutati.

  Gli utenti possono preferire la forma mostrata nell’equazione (1) di cui sopra, per scopi diversi dalla riduzione dei dati del rilievo. Per questi scopi, durante l’elaborazione è sufficiente rivalutare il primo elemento di dati alla fine della traversata, o fornire set di dati che ripetono il primo elemento di dati come ultimo.

• Ecco una funzione Python completa e funzionante:
  

  def find_area(array): a = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) ox,oy = x,y return a/2 

• L’argomento “array” di cui sopra è un insieme di coordinate cartesiane $x,y$, cioè ((10,10,10)).e. ((10,10),(10,20),(20,20),(20,10),(10,10)). Notate su questa serie di dati che il primo dato è ripetuto alla fine.

• Ecco una funzione Python leggermente più complessa che calcola sia l’area che la lunghezza del perimetro:
  

  def find_area_perim(array): a = 0 p = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) p += abs((x-ox)+(y-oy)*1j) ox,oy = x,y return a/2,p 

• Anche questo promemoria: per entrambi gli esempi di codice di cui sopra, in applicazioni diverse dalla riduzione dei dati di rilevamento del territorio, il set di dati fornito dovrebbe includere una copia del primo dato come ultimo, cioèCioè la figura dovrebbe essere esplicitamente chiusa.

• Ho scelto Python per questi esempi perché un listato Python massimizza il significato algoritmico minimizzando il cruft.

• Le funzioni di cui sopra possono essere facilmente convertite in altri linguaggi, quasi direttamente – tranne la somma del perimetro mostrata sopra, che sfrutta il fatto che Python supporta i numeri complessi. Per i linguaggi che non supportano i numeri complessi, si può creare il risultato del perimetro in questo modo:

  C/C++: p += sqrt(pow(x-ox,2)+pow(y-oy,2));

  Java: p += Math.sqrt(Math.pow(x-ox,2)+Math.pow(y-oy,2));

• Formalmente, la lunghezza del perimetro è la somma delle grandezze dei vettori:
  

  (3) Lunghezza del perimetro $\displaystyle P = \sum_{i=m}^{n-1}{sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2}}$

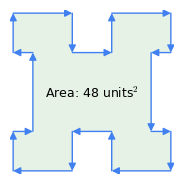
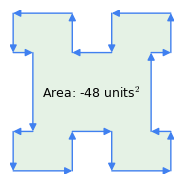Figura 1: Vettori in senso orario vs. vettori in senso antiorario

Ecco alcune importanti proprietà di questo metodo:

• Il vertice di origine scelto all’interno del poligono è irrilevante per il calcolo dell’area o del perimetro, solo che la figura sia chiusa, cioè l’ultima coordinata deve essere uguale a quella del poligono.Cioè l’ultima coordinata deve essere uguale alla prima.
• “Regola in senso orario”: l’ordine dei vettori è significativo – se il perimetro è percorso in senso orario, il risultato dell’area è positivo, se in senso antiorario, è negativo (Figura 1). È questa proprietà del metodo che sottrae l’area delle inflessioni da una figura complessa come nella Figura 1 – le “inflessioni” rappresentano una traversata in senso antiorario all’interno del poligono.
• Molte applicazioni di questo metodo usano fonti di dati originali costituite da vettori polari (un esempio sono le descrizioni legali del catasto), ma questo metodo richiede coordinate cartesiane. La conversione da coordinate polari a cartesiane è banale, ma è importante tenere a mente questo requisito.
• Inoltre, per un calcolo accurato dell’area, il poligono descritto dovrebbe essere una figura chiusa – l’ultima coordinata dovrebbe essere uguale alla prima. Per le applicazioni che utilizzano dati di campo costituiti da vettori di lunghezza che sono successivamente convertiti in forma cartesiana, è una buona idea confrontare le coordinate cartesiane iniziali e finali – dovrebbero essere uguali. Per esempio, i vecchi rilievi del terreno (prima dell’era dei computer a basso costo) regolarmente falliscono questo test.

Questa sezione è un computer di area/perimetro completamente funzionale che può elaborare coppie di dati di coordinate cartesiane o polari inserite, o descrizioni legali di rilievo. Basta scegliere un tipo di dati (coordinate cartesiane x,y, coordinate polari m,θ o una descrizione legale del rilievo) e inserire (o incollare) i dati nell’area di inserimento dati sottostante. Puoi anche selezionare serie di dati campione per familiarizzare e fare pratica.

A causa di problemi di sicurezza del browser, per evitare un’eccessiva digitazione e per importare quantità significative di dati da un’altra fonte, i lettori dovranno usare gli appunti del loro sistema. Basta copiare i dati negli appunti dell’applicazione di origine, poi cliccare sull’area di inserimento dati in basso e premere Crtl+A per selezionare tutto, Ctrl+V per copiare i dati da un’altra fonte, e Ctrl+C per copiare i propri dati inseriti. La maggior parte dei browser include anche funzioni di appunti come voci di menu.

Scegliete il tipo di dati:

cartesiano (x,y)

polare (m,θ)

Descrizione del rilievo

Area inserimento dati: Seleziona tutto: Ctrl+A | Copia: Ctrl+C | Incolla: Ctrl+V

Area del grafico:

Spiacente – il tuo browser non supporta la capacità grafica richiesta da questa funzione –
considera di installare Google Chrome o Firefox.

Opzioni:

Linee

Frecce

Origine

Centro

Lunghezza Unità:

Larghezza linea:

Inverso

Risultati:Seleziona tutto: Ctrl+A | Copia: Ctrl+C | Incolla: Ctrl+V

Il computer area/perimetro ha tre modalità di ingresso:

• Coppie di coordinate cartesiane (x,y):

  • Ogni coordinata è una posizione bidimensionale con una parte orizzontale (x) e verticale (y) (una coordinata cartesiana).
  • Le coordinate non sono cumulative – ognuna descrive indipendentemente la sua posizione.
  • Così un quadrato sarebbe:
    • 0,0 (origine)
    • 0,100 (su)
    • 100,100 (destra)
    • 100,0 (giù)
    • 0,0 (ritorno all’origine)
  

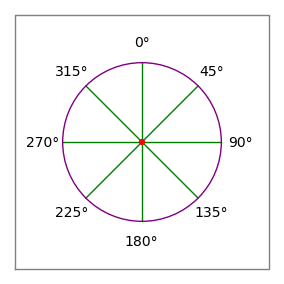  Figura 2: Rosa dei venti

  • Le virgole nell’esempio precedente servono solo a raggruppare le coppie di dati per il lettore – non hanno alcun significato per l’analizzatore di dati del computer di zona.
  • Il parser è abbastanza robusto che l’esempio di cui sopra può essere incollato nell’area di inserimento dati del computer e funzionerà (prova).
  • L’unica limitazione è che i commenti esplicativi non possono contenere numeri.

• Coppie di coordinate polari (m,θ):

  • Ogni coordinata consiste in una distanza e un angolo in gradi (un vettore polare).
  • Gli angoli seguono la convenzione della bussola – 0 gradi è in alto o “nord”, 90 gradi è a destra o “est” (Figura 2).
  • A differenza della forma cartesiana precedente, queste coordinate sono cumulative – ogni nuovo vettore aggiunge alla posizione attuale.
  • Così un quadrato sarebbe:
    • 100,0 (su)
    • 100,90 (destra)
    • 100,180 (giù)
    • 100,270 (indietro all’origine)
  • Come prima, questo esempio funzionerà se incollato nell’area di inserimento dati del computer e la modalità polare selezionata.
  • Nota sulle coordinate polari che l’origine è implicita e preimpostata a x = 0, y = 0.
  

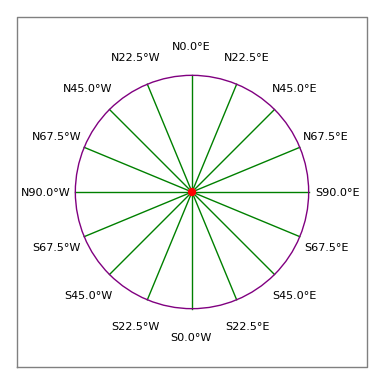  Figura 3: Rosa dei venti del geometra

• Descrizione legale:

  • Prima, una spiegazione della relazione tra la selezione “Unità di lunghezza” e la visualizzazione dei risultati:
    • Per ogni poligono, una lista di risultati di area è calcolata usando un set fisso di unità di area comuni (piedi2, metri2, ecc.). Affinché questa lista di aree sia significativa, le unità di lunghezza in ingresso devono essere note.
    • In modalità cartesiana e polare, le voci dei dati non hanno unità, quindi l’utente sceglie quali unità assegnare alle lunghezze. Così, quando l’utente cambia le unità di lunghezza, i valori di area cambiano, le etichette di lunghezza cambiano, ma i valori di lunghezza no.
    • In modalità Survey, la descrizione legale contiene unità di lunghezza (piedi, metri, ecc.) il che significa che le unità di lunghezza sono predefinite dalla fonte. Quindi quando l’utente cambia le unità di lunghezza, questo cambia le etichette e i valori di lunghezza, non i valori di area.
  • L’analizzatore di descrizione del sondaggio è di gran lunga il meno affidabile dei tre metodi di analisi dei dati – è più un esperimento che un metodo robusto di conversione dei dati.
  • Ho scritto questo parser scaricando un certo numero di descrizioni legali (che sono fornite come esempi nella calcolatrice di cui sopra) e sintonizzando il codice del parser fino a quando tutti potevano essere decodificati con successo.

  I criteri per il “successo” erano che il risultato avesse la stessa area quadrata come le affermazioni della descrizione, e che la figura “chiudesse”.

  • Il termine “chiusura”, e in particolare l’errore di chiusura, è usato nel lavoro di indagine per descrivere il grado in cui il punto finale della traversata di indagine è uguale al punto iniziale. Questo è raramente vero in realtà – gli errori di chiusura di solito derivano da errori nel lavoro sul campo, e le indagini più vecchie, pubblicate prima dell’avvento della potenza del computer a buon mercato, tendono ad avere chiusure piuttosto scarse, così come stime selvaggiamente imprecise di area quadrata.
  • Una descrizione legale è un modo formale per descrivere un appezzamento di terreno – la sua forma e sintassi è nata nel corso di decenni da convenzioni reciprocamente accettate, in qualche modo arbitrarie, condivise dai geometri.
  • Per questo computer area/perimetro i dati inseriti devono seguire alcune rigide convenzioni che alcune, ma non tutte, descrizioni legali aderiscono. Gli elementi essenziali sono:
    • L’esistenza della frase “punto di inizio”, che separa alcuni contenuti preliminari da quelli che descrivono le dimensioni della particella descritta. Alcuni documenti dicono “True point of beginning”, altri dicono “Real point of beginning” e altri ancora dicono “Point of beginning”. Un parser di successo deve rimuovere il contenuto prima di questa frase e mantenere tutto quello dopo di essa.
    • Una serie di frasi che descrivono un tipo speciale di vettore polare usato dai geometri:
      • La parola “Nord” o “Sud”, o la sua abbreviazione “N” o “S”.
      • Quindi un angolo espresso in gradi, minuti e secondi.
      • Quindi la parola “Est” o “Ovest”, o la sua abbreviazione “E” o “W”.
      • Poi una distanza.
      • Poi un’unità di distanza – piedi, metri, ecc.
  • Ecco alcuni esempi diversi di vettori geometri dalle descrizioni legali di esempio:
    • N 2°0’0″ W – 63.50 piedi
    • N90°00’00 “W LUNGO UNA LINEA PARALLELA CON DETTA LINEA NORD A DISTANZA DI 6.00 PIEDI
    • Nord 0°06’O0″ West una distanza di 554.86 piedi
    • S. 22 gradi 41′ 55″ E. 174.10 piedi
  • Si noti che gli esempi precedenti hanno tutti una sintassi diversa. Ci sono molte descrizioni legali esistenti che questo parser non decodifica con successo, solo perché non ho cercato di incorporare la loro sintassi. Ma è importante aggiungere che un parser veramente robusto per la moltitudine di descrizioni legali esistenti dovrebbe essere intelligente come Watson.
  • Gli utenti di questo computer di area/perimetro potrebbero voler evitare di inviare descrizioni legali in testo semplice e sperare che il parser lo capisca. Per fare inserimenti diretti a mano (o per creare una lista di attraversamenti altrove per l’importazione), usate questa convenzione:
    • Ricorda che una voce di traversata accettabile consiste nella parola “Nord” o “Sud”, o la lettera “N” o “S”, seguita da un massimo di tre numeri che forniscono gradi, minuti e secondi di angolo, seguita dalla parola “Est” o “Ovest” o la lettera “E” o “W”, seguita da una distanza, seguita da una unità di distanza.
    • Così una voce accettabile sarebbe “N 30 15 45 W 100 piedi”, che significa una traversata di 100 piedi che punta 30 gradi, 15 minuti e 45 secondi a ovest del nord (cioè circa 330 gradi bussola, vedi Figura 3).
    • Le voci di minuti e secondi possono essere saltate se sono uguali a zero, o se la voce è in gradi decimali, o gradi e minuti decimali.
  • Non è difficile convertire una descrizione legale stampata in tali voci, e ci sono diversi modi per rilevare gli errori. Dopo aver inserito tutte le traverse, se la figura non ha errori di chiusura e riporta la stessa area quadrata dell’originale, è probabile che le voci siano corrette (o che abbiano gli stessi errori della descrizione originale).
  • Dopo aver inserito una descrizione legale in questo modo, se c’è un errore di chiusura inaccettabile o l’area quadrata è sbagliata, ricorda che i dati originali potrebbero essere sbagliati. Esiste un numero qualsiasi di descrizioni legali che non sono mai state controllate con un metodo informatico come questo, e che non sono mai state corrette.

Scorrendo gli esempi cartesiani (x,y), nota il rapporto tra area e perimetro delle diverse forme. Il “poligono di forma strana” ha un rapporto intermedio, il cerchio ha il rapporto più piccolo, e lo spazio di Hilbert ha di gran lunga il rapporto più grande. Questo rapporto si estende alle dimensioni superiori, dove una sfera è nota per avere il maggior volume per superficie.

Per quanto riguarda l’esempio del cerchio – è un “cerchio unitario”, un cerchio con un raggio di uno. Per l’esempio fornito, l’area approssima $\pi$ e il perimetro approssima $ 2\pi$, i valori giusti per un cerchio unitario. Affinché questi valori siano più che approssimazioni, per essere esattamente uguali a $\pi$ e $2\pi$, il numero di lati del poligono dovrebbe essere infinito. Ho deciso di non farlo. 🙂

L’esempio dello spazio di Hilbert è stato generato usando un algoritmo Sage con una scelta di ordine modesto (per evitare di generare troppi dati). In linea di principio uno spazio di Hilbert può avere un rapporto infinito tra perimetro e area in due dimensioni, o tra superficie e volume in tre dimensioni. Per vedere quanto complesso può diventare uno spazio di Hilbert, clicca qui per vedere uno spazio di Hilbert di ordine 7.

Nota sull’esempio di Hilbert che l’area calcolata è vicina a 1/2 per una superficie 1×1. Idealmente, senza la necessità di convertire una figura di linea in una figura di area e con il giusto algoritmo, l’area della superficie sarebbe esattamente 1/2 di quella di un quadrato delle stesse dimensioni.

Il modo di immissione polare è più o meno uguale alla grafica Turtle, se si sostituisce zero gradi con “su”, 90 gradi con “destra”, ecc. Usare la modalità di inserimento polare è un modo semplice per costruire a mano una forma complessa, perché le distanze e gli angoli sono più facili da tenere traccia delle coordinate cartesiane.

Ho usato per la prima volta il metodo di calcolo dell’area del terreno sopra descritto anni fa quando vivevo nell’Oregon rurale, circondato da persone che avevano bisogno di conoscere l’area e il perimetro delle loro proprietà. Ho incontrato molti esempi scioccanti in cui gli agenti immobiliari imbrogliavano sfacciatamente le persone che non avevano modo di scoprire cosa stava succedendo. In un certo numero di occasioni avrei calcolato un’area da una descrizione legale, solo per scoprire che l’affermazione dell’atto di garanzia sulla superficie in acri era selvaggiamente imprecisa – e sempre più alta della realtà.

In un’occasione mi fu chiesto di dividere una proprietà in due sezioni uguali e creare descrizioni legali per ciascuna. Dato che avevo un Apple II appena acquistato (che aveva la potenza di elaborazione di un moderno temperamatite), questo fu molto facile – ma mentre lavoravo mi resi conto che la superficie totale era sbagliata di circa tre acri, circa il 25% del totale. Mi confrontai con la società di titoli di proprietà, che mi rispose sfacciatamente: “Vedi qui, dove l’atto dice ‘più o meno’?”

In un’altra occasione iniziai l’acquisto di un terreno, ma messo in guardia dall’esperienza di cui sopra, quando ricevetti la polizza di proprietà decisi di inserire la descrizione legale nel mio programma per vedere se l’indicazione dell’acro fosse accurata. Ma con orrore, ho scoperto che tutte le polizze per i titoli di proprietà per i lotti in quella sezione avevano la stessa descrizione legale – della prima proprietà censita. Si è scoperto che la società di sviluppo territoriale aveva deciso di risparmiare denaro facendo il rilievo di uno solo delle dozzine di lotti offerti in vendita, e di includere quella descrizione legale in tutte le polizze di proprietà. Erano sicuri che l’avrebbero fatta franca – dopo tutto, chi sa qualcosa di matematica?

Dopo aver discusso con la società che si occupa dei titoli di proprietà e lo sviluppatore, cercando di persuaderli a pagare per i rilievi in modo che le descrizioni legali non fossero cortesi finzioni, ho rinunciato e ho deciso di non comprare il terreno. È stato come scoprire come si fa la salsiccia – è possibile sapere troppo.

• 04.15.2013 Versione 1.3. Aggiunta una spiegazione dettagliata del formato di dati predefinito, cioè liste che ripetono il primo punto di dati come ultimo.
• 03.24.2013 Versione 1.2. Ulteriormente ottimizzato l’analizzatore della descrizione del sondaggio, aggiunti più campi di dati di risultato.
• 03.23.2013 Versione 1.1. Migliorato l’analizzatore delle descrizioni legali per gestire più tipi di descrizioni, aggiunto il selettore delle unità di lunghezza e un elenco dei risultati delle aree in unità comuni.
• 03.22.2013 Versione 1.0. Rilascio pubblico iniziale.