L’equazione logistica (talvolta chiamata modello di Verhulst o curva di crescita logistica) è un modello di crescita della popolazione pubblicato per la prima volta da Pierre Verhulst (1845, 1847). Il modello è continuo nel tempo, ma una modifica dell’equazione continua in un’equazione di ricorrenza quadratica discreta nota come mappa logistica è anche ampiamente utilizzata.
La versione continua del modello logistico è descritta dall’equazione differenziale
 |
(1)
|
dove 
è il parametro malthusiano (tasso di crescita massima della popolazione) e 
è la cosiddetta capacità di carico (cioè, la popolazione massima sostenibile). Dividendo entrambi i lati per 
e definendo 
si ottiene l’equazione differenziale
 |
(2)
|
che è nota come equazione logistica e ha soluzione
 |
(3)
|
La funzione 
è talvolta nota come funzione sigmoide.
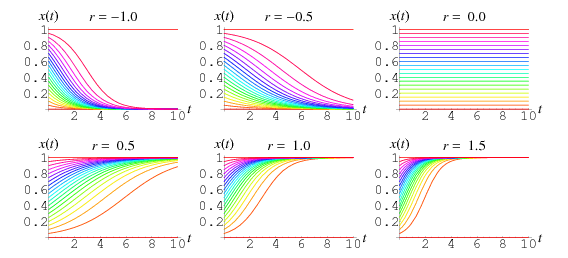
Mentre 
è di solito costretta ad essere positiva, i grafici della soluzione di cui sopra sono mostrati per vari valori positivi e negativi di 
e condizioni iniziali 
che vanno da 0,00 a 1,00 in passi di 0,05.
La versione discreta dell’equazione logistica (3) è conosciuta come la mappa logistica.
La curva
 |
(4)
|
ottenuta dalla (3) è talvolta conosciuta come la curva logistica. Allo stesso modo, una forma normalizzata dell’equazione (3) è comunemente usata come una distribuzione statistica conosciuta come distribuzione logistica.