Vita media

Figura 1. Un grafico che mostra il decadimento di un nucleo radioattivo nel tempo. Il tempo che impiega la massa o l’attività della sorgente (il numero di eventi di decadimento al secondo) a scendere al 50% è il tempo di dimezzamento. Il tempo di dimezzamento in questa immagine è di 1 anno.

L’emivita è il tempo che impiega la metà del valore originale di una certa quantità di un elemento radioattivo a decadere. Inoltre, un’emivita è il tempo che impiega l’attività di una sorgente a scendere alla metà del suo valore originale. La seconda legge della termodinamica, in particolare l’affermazione del disordine, può essere usata per aiutare a capire perché si verifica il decadimento radioattivo. Questa affermazione dice che l’entropia di un sistema chiuso non può mai diminuire, il che significa che le cose devono cadere ulteriormente nel disordine, non nell’ordine. Questo processo è noto come “decadimento” e la seconda legge aiuta a chiarire perché la materia si rompe in uno stato sempre meno organizzato nel tempo. Parte di questo processo include certi tipi di atomi che si rompono in nuovi e diversi tipi di atomi ad un tasso misurabile conosciuto come decadimento radioattivo.

Tutti i materiali radioattivi hanno nuclei instabili al loro interno. Inoltre, ci sono anche alcuni nuclei all’interno della sostanza che sono già nel loro stato stabile, ma la proporzione di nuclei stabili e instabili in un campione può variare. I nuclei stabili nel campione sono immutabili (e in uno stato energetico stabile), ma i nuclei instabili subiranno una sorta di decadimento nucleare nel tempo per diventare stabili. Questo si traduce in un’emissione di qualche forma di radiazione. Poiché l’emivita è una misura del tempo, l’emivita è un valore che determina quanto tempo ci vorrà per questa riduzione a uno stato energetico più stabile.

Sostanze diverse sperimentano una perdita della loro radioattività più rapidamente di altre. Alcuni elementi radioattivi possono far decadere metà dei loro nuclei instabili in meno di un secondo. Per esempio, il krypton-101 ha un tempo di dimezzamento di circa un decimilionesimo di secondo. Al contrario, alcuni elementi hanno emivite straordinariamente lunghe e impiegano miliardi di anni per decadere. L’uranio-238 ha un’emivita di 4,51 miliardi di anni. Ciò significa che l’uranio-238 impiegherebbe miliardi di anni per decadere in un rapporto di metà uranio-238 e metà torio-234. L’uranio-235 (un altro isotopo naturale dell’uranio) ha un’emivita più breve dell’uranio-238, cioè solo ~700 milioni di anni.

Equazione

C’è un’equazione che viene spesso usata per determinare quanto di una certa sostanza radioattiva rimane dopo che è passato un dato tempo. Questo è determinato da proprietà come il tempo di dimezzamento della sostanza, e quanto della sostanza c’era inizialmente. L’equazione usata è:

dove:

• è la quantità di sostanza dopo che il tempo è passato
• è la quantità di sostanza iniziale
• è la quantità di tempo che è passato
• è l’emivita della sostanza

Inoltre, una simile equazione può essere usata per mostrare come l’attività della sostanza diminuisce nel tempo. Quando questo viene espresso, l’equazione prende la forma:

dove:

• è l’attività della sostanza dopo che il tempo è passato
• è l’attività iniziale della sostanza
• è la quantità di tempo che è passato
• è l’emivita della sostanza

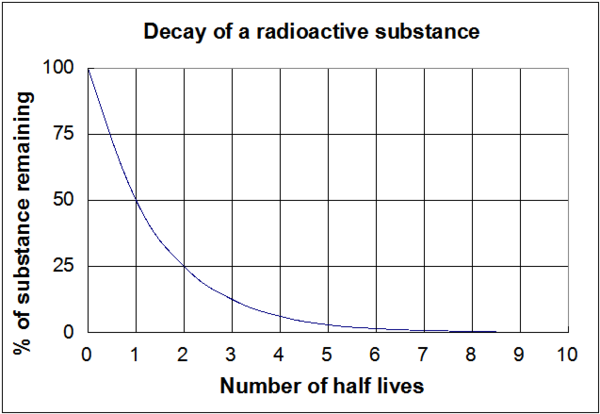
Il grafico mostrato nella figura 1 è una rappresentazione visiva di queste equazioni sopra. E’ importante notare che indipendentemente dalla lunghezza effettiva del tempo di dimezzamento (che sia di milioni di anni o di pochi nanosecondi) la forma del grafico sarà la stessa.

La conoscenza dei tempi di dimezzamento è parte di come i geologi datano le rocce con la datazione radioisotopica.