Between Borders

Weleens een document gedownload of een bestand van een vriend gekregen, maar het werd slecht afgedrukt? Er zijn veel mogelijke oorzaken voor dergelijke problemen: verschillende lettertypen voor de maker en de printer; verschillende besturingssystemen en verschillende versies van dezelfde besturingssystemen die beperkingen in zogenaamde cross-platform standaarden blootleggen; verschillende printer-engines, vooral bij het overschakelen tussen inkjet en laser; enzovoort.

Een vaak over het hoofd geziene oorzaak van problemen is echter het verschil in papierformaat. Wanneer mensen in de VS en Canada naar een vel papier grijpen om op te schrijven of te printen, is de kans groot dat ze naar een stuk Letter-papier grijpen (ook bekend als US Letter), van 8,5 bij 11˝. Als mensen overal elders een vel papier pakken om op te schrijven of te printen, pakken ze, op een enkele uitzondering na, een stuk papier van A4-formaat (210 mm bij 297 mm).

Een snelle omrekening tussen inches en millimeters laat zien dat de twee maten niet zoveel verschillen:

	Millimeters		Inches
	Breedte	Lengte	Breedte	Lengte
A4	210.0	297.0	8.26	11.69
Letter	215.9	279.4	8.50	11.00

En een schaalweergave van elke paginagrootte versterkt de gelijkenis van de twee papierformaten.

Wat de vraag doet rijzen, waarom überhaupt het verschil? Als beide maten willekeurig zijn, waarom dan nog het verschil handhaven. De antwoorden zijn lang en ingewikkeld, en vallen grotendeels buiten het bestek van dit artikel. In de kern komt het echter op één ding neer: A4 is geen arbitrair formaat.

A4 Beschreven

A4 maakt deel uit van de ISO 216-reeks van verwante papierformaten die meer algemeen bekend staan als de A-serie. Deze serie begint met het grote A0 vel en een snelle blik op dit grote vel papier laat zien waarom deze verschillende vellen de afmetingen hebben die ze hebben.

A0 vellen papier zijn 841mm bij 1189mm. Nogmaals, schijnbaar willekeurig. Vermenigvuldig de twee getallen echter met elkaar, en het wordt iets duidelijker: 841 * 1189 = 999.949mm in het kwadraat of 0,999949m in het kwadraat (d.w.z. net iets minder dan een vierkante meter papier). Voor alle praktische doeleinden bevat een A0 vel een vierkante meter papier.

Waarom dan geen vel van 1m bij 1m? Vanwege een andere niet-arbitraire overweging: de hoogte-breedte verhouding van elk vel.

1189/841 = 1,413793103448276. Niet bijzonder gedenkwaardig, tenzij je toevallig wiskundig handig genoeg bent om de overeenkomst te zien met √2 (de vierkantswortel van 2, een irrationaal getal dat zo begint: 1.414213562373095). Rond beide getallen af op vier significante cijfers en je krijgt dezelfde waarde: 1,414.

Dus, de hoogte-breedteverhouding van een A0 vel papier is, alweer voor praktische doeleinden, één als de vierkantswortel van twee of 1:√2. En weer hoor ik de kreten: ‘en wat dan nog!’

Een verhouding van 1:√2 is meer dan een wiskundige eigenaardigheid. Het heeft geen mooie naam, zoals de beroemde Gulden Snede of Gulden Snede. Het heeft echter wel een handige eigenschap. Deel een rechthoek met zijden 1:√2 langs de langste zijde en de kleinere rechthoek die je maakt heeft dezelfde hoogte-breedteverhouding. (Markus Kuhn stelde in een briefwisseling voor om de verhouding de Lichtenberg-verhouding te noemen, naar professor Georg Christoph Lichtenberg, de Duitse verlichtingsfiguur die in 1786 de verhouding voor het eerst voorstelde als basis voor papierformaten.)

Terugkomend op de verhouding (genoemd of niet) en zijn handige eigenschap: als we beginnen met een verdomd groot vel A0 papier:

We kunnen gemakkelijk, en snel, alle andere A-serie formaten afleiden door aldus te vouwen of te delen:

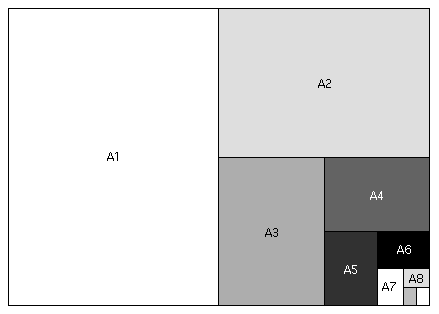
In minder visuele termen: elk vel papier uit de A-serie is even lang als het eerstvolgende grotere vel breed is en half zo breed als het eerstvolgende grotere vel lang is. Dat wil zeggen:

Sheet name	Width (mm)	Length (mm)
A0	841	1189
A1	594	841
A2	420	594
A3	297	420
A4	210	297
A5	148	210
A6	105	148
A7	74	105
A8	52	75

Er zijn nog andere voordelen aan deze verhouding tussen papierformaten, niet in het minst wanneer u een bepaalde lay-out wilt schalen. Als u zich ooit hebt afgevraagd waarom fotokopieerapparaten een verkleiningsoptie van 71% bieden, hoeft u zich dat niet meer af te vragen: 0,71 is ongeveer gelijk aan (√2)/2 of √0,5. Dit maakt de optie perfect voor het verkleinen van een A3-layout op een A4-vel, of een A4-layout op een A5-vel of, nog gebruikelijker, het netjes en zonder gedoe verkleinen van twee A4-vellen naast elkaar – bijvoorbeeld in een dagboek – op één A4-vel. De al even gebruikelijke 141%-optie is natuurlijk perfect voor het vergroten van een vel uit de A-serie naar het volgende (bijvoorbeeld van A4 naar A3). Het belangrijkste is dat, omdat elk vel dezelfde hoogte-breedteverhouding heeft, objecten hun relatieve vorm behouden: vierkanten worden geen rechthoeken en cirkels worden geen ellipsen.

Niet in de laatste plaats maakt deze constante verhouding papier uit de A-serie eenvoudiger om mee te werken dan oudere papierformaten zoals Brief (13˝ bij 16˝, en de bron van de ‘briefjes’ die advocaten nog steeds gebruiken) of Foolscap (27˝ bij 17˝) en het daarvan afgeleide, bijna lettergrote Foolscap Quarto (13˝ bij 16˝, en de bron van de ‘briefjes’ die advocaten nog steeds gebruiken).5˝ bij 8,5˝, gewoonlijk, zij het ten onrechte, “Foolscap” genoemd).

Voeg daarbij een duidelijk verband met het metrieke (of, beter gezegd, het SI-) meetsysteem en de toename van de populariteit van papier uit de A-serie is vrij gemakkelijk te begrijpen: naarmate de wereld langzaam maar zeker is overgegaan op het metrieke stelsel, is papier uit de A-serie populairder geworden. In Australië bijvoorbeeld werd het metrieke stelsel officieel ingevoerd in 1974, hetzelfde jaar dat papier van de A-serie (en verwante series zoals de C-serie voor enveloppen) de standaard begon te worden.

US Letter Beschreven

De duidelijke band met het metrieke stelsel is ook een gedeeltelijke verklaring voor het blijvende gebruik van papier in Letter-formaat in de VS en Canada. De VS is bijna het enige land dat nog niet is overgeschakeld van niet-metrieke maten, waardoor de bijzondere voordelen van A4 minder duidelijk zijn. Bovendien zijn de Amerikaanse papierformaten weliswaar zo willekeurig als soms wordt beweerd, maar niet onmogelijk om mee te werken.

Er is geen afgeleid uitgangspunt (gelijk aan de 1 vierkante meter voor A0) voor Amerikaanse papierformaten, maar de twee populairste formaten – Letter en Tabloid – maken deel uit van een oude norm van het American National Standard Institute voor technisch tekenpapier. Deze norm (ANSI/ASME Y14.1) kende vijf papierformaten die heen en weer slingerden tussen twee verschillende beeldverhoudingen:

Sheet name	Width (˝)	Length (˝)	Aspect Ratio
A (Letter)	8.5	11.0	1.294
B (Tabloid)	11.0	17.0	1.545
C	17.0	22.0	1.294
D	22.0	34.0	1.545
E	34.0	44.0	1.294

Dit is niet zo elegant of handig als papier uit de A-serie, maar het vergroten en verkleinen van bepaalde lay-outs met behoud van de interne verhoudingen is niet bijzonder moeilijk. U hoeft alleen maar een papierformaat over te slaan als u in beide richtingen werkt.

Het is de moeite waard op te merken dat geen van beide beeldverhoudingen bijzondere wiskundige eigenschappen heeft. En dat er twee beeldverhoudingen zijn is niet verwonderlijk: vouw een rechthoek in tweeën die geen zijden heeft in de verhouding 1:√2 en de zijden van de kleinere rechthoek zullen in een andere verhouding tot elkaar staan. Vouw de kleinere rechthoek nogmaals dubbel en de zijden van deze derde rechthoek zullen in dezelfde verhouding staan als die van de rechthoek waarmee je begon.

Die eenvoudige eigenschap is de reden waarom rechthoeken met zijden in de verhouding 1:√2 zo handig zijn: het zijn de enige rechthoeken waarbij de twee verhoudingen die je krijgt door heen en weer te vouwen gelijkwaardig en onderling verwisselbaar zijn.

En alleen al het nut van deze onderlinge verwisselbaarheid is de reden waarom ik denk dat oudere papierformaten zoals US Letter uiteindelijk zullen verdwijnen, zelfs in de VS. De huidige versie van de ANSI-norm bijvoorbeeld – ANSI/ASME Y14.1m-1995 – erkent de oudere papierformaten alleen voor legacy-doeleinden, en stelt papier van de A-serie vast als de voorkeursnorm in de VS voor technische tekeningen.

Verder heb ik begrepen dat papier van de A-reeks – vooral A4 – langzaam de norm wordt in Amerikaanse hogescholen en universiteiten, al was het alleen maar om het voor studenten en personeel gemakkelijker te maken artikelen uit (onvermijdelijk A4-formaat) tijdschriften te fotokopiëren.

Finitief eist de globalisering haar tol: Amerikaanse bedrijven die zaken doen met ambtenaren buiten de VS (vooral de EU) vinden dat ze voorstellen, offertes, schema’s enzovoort op papier van de A-serie moeten indienen.

Op zoek naar het juiste bestandsformaat

Wat allemaal goed en wel is, maar het onmiddellijke probleem niet oplost: hoe kan iemand die vandaag documenten ontwerpt voor gebruik in Noord-Amerika en de rest van de wereld ervoor zorgen dat zijn ontwerpen niet mislukken door de verschillen tussen A4- en Letter-papier?

Ten eerste, en onder verwijzing naar alle andere mogelijke oorzaken van problemen waarnaar hierboven wordt verwezen, verstuur of verspreid geen documenten die afhankelijk zijn van externe factoren om goed te worden weergegeven en afgedrukt. Dus, geen Word documenten, geen Quark XPress documenten, geen PageMaker bestanden, geen AppleWorks bestanden enzovoort.

Zelfs als u er zeker van bent dat de persoon die uw bestanden ontvangt dezelfde versie van dezelfde applicatie heeft, alle lettertypes die u heeft gebruikt en dezelfde printer gebruikt, geen van deze bestandsformaten is veilig om over de papierformaat scheidslijn te sturen. Ze falen op dit laatste punt omdat ze nog steeds afhankelijk zijn van externe factoren om te worden weergegeven en afgedrukt.

Bij voorbeeld, een Word-document geformatteerd met 25 mm marges op Letter-formaat papier zal de tekst die het bevat opnieuw laten vloeien wanneer het wordt geopend op een computer die standaard documenten op A4 weergeeft. Zelfs rechttoe rechtaan proza in een enkele kolom zal onder dergelijke omstandigheden opnieuw worden gepagineerd. Alles wat ingewikkelder is (b.v. een combinatie van tekst en afbeeldingen of een scenario) zal onder dergelijke omstandigheden vrijwel zeker verkeerd worden weergegeven aan de ontvangende kant.

(Ik zou zelfs zo ver willen gaan om te suggereren dat het verzenden van discrete tekstbestanden (d.w.z. een tekstbestand dat als bijlage bij een e-mailbericht wordt verzonden in plaats van deel uit te maken van de inhoud van het bericht) uit den boze is, al was het maar vanwege het nog steeds bestaande probleem “welke regeleinde hebben zij gebruikt”, maar dit is een apart probleem.)

De lijst van niet te verzenden documenttypen is tamelijk lang. De lijst van documenttypes die wel mogen worden verzonden is vrij kort: ruwe PostScript-bestanden en Adobe Acrobat (aka ‘pdf’)-bestanden.

Beide bestandsformaten coderen en fixeren de ruimtelijke relaties tussen individuele elementen op een pagina. Het genereren van ruwe PostScript-bestanden is betrekkelijk eenvoudig: stel uw computer in om af te drukken op een PostScript-compatibele printer (zelfs als u er geen hebt) en ‘print’ vervolgens uw document naar een bestand. Het bestand dat op deze manier wordt geproduceerd is veilig om te verzenden. Helaas kan het bestand niet op een scherm worden bekeken zonder een beetje geekerd te worden en kan het alleen betrouwbaar worden afgedrukt door het naar een PostScript-compatibele printer te sturen.

Acrobat-bestanden: het beste van het slechte

Waardoor Acrobat-bestanden standaard de beste optie zijn. Ik zeg “standaard” omdat Acrobat files niet mijn eerste keus zouden zijn. Het bestandsformaat is slechts half-open en Acrobat bestanden zijn groter dan ik zou willen, als je ze vergelijkt met de hoeveelheid informatie die erin is gecodeerd. Er is ook nog het kleine puntje van de kosten.

Als je eenmaal een exemplaar van Word hebt gekocht, kost het niets meer om een Word document te maken. Hetzelfde geldt voor andere hulpmiddelen voor het maken van documenten, zoals Quark XPress, WordPerfect, PageMaker, enzovoort.

Acrobat daarentegen wordt niet op de markt gebracht of verkocht als een hulpmiddel voor het maken van documenten. Adobe beschrijft Acrobat als:

een universeel bestandsformaat dat alle lettertypen, opmaak, afbeeldingen en kleur van elk brondocument behoudt, ongeacht de toepassing en het platform waarmee het is gemaakt

Ruwweg gezegd is Acrobat een opvolger van PostScript. Net als PostScript is Acrobat een programmeertaal die is ontworpen om precies te definiëren waar op een pagina objecten moeten worden geplaatst. Acrobat bevat ook een aantal soms handige hulpmiddelen om deze goed gedefinieerde pagina’s om te zetten in formulieren waarin nieuwe gegevens direct kunnen worden verwerkt.

Vanuit het perspectief van iemand die geformatteerde pagina’s wil distribueren, is het belangrijkste verschil tussen Acrobat en PostScript de Adobe Acrobat Reader. Waar Adobe geld vraagt om een PostScript interpreter in hun producten op te nemen (een van de redenen waarom PostScript printers meer kosten dan niet-PostScript printers), is de Acrobat interpreter (d.w.z. Acrobat Reader) freeware, beschikbaar om te downloaden en inbegrepen bij de aankoop van bijna elke computer of besturingssysteem.

Wat geweldig klinkt totdat je een Acrobat bestand moet maken en je je realiseert dat Adobe alleen maar de kosten veranderd heeft. PostScript-bestanden zijn gratis te maken (PostScript-printerdrivers zijn gratis) maar kosten geld om te bekijken (PostScript-printers zijn duur in vergelijking met niet-PostScript-printers).

Acrobat-bestanden zijn gratis te bekijken (Acrobat Reader is gratis) maar kosten geld om te maken (geen Adobe-tools voor het maken van Acrobat-bestanden zijn gratis).

Acrobat-bestanden maken

Adobe biedt verschillende hulpmiddelen om Acrobat-bestanden te maken, te beginnen met een web-gebaseerde dienst die u voor niets kunt uitproberen en waarop u zich kunt abonneren voor US$10,00/maand of US$100/jaar. Deze dienst is alleen beschikbaar voor inwoners van de VS en Canada.

Voor de rest van ons (en voor mensen uit de VS en Canada die liever een voorschot betalen dan een doorlopend abonnement) is er Adobe Acrobat, waar Adobe US$250,00 voor vraagt, maar dat in de winkel te koop is voor ongeveer US$220,00.

Adobe biedt ook een reeks duurdere producten in de Acrobat-familie die zijn ontworpen rond de behoeften van de workflow van bedrijven.

En, voor de avonturiers, er zijn verschillende derde partijen die gebruik maken van Acrobat’s semi-open karakter om Acrobat creatie gereedschappen aan te bieden zonder Adobe’s formele zegel van goedkeuring. Een goede plaats om te beginnen met zoeken naar info over dergelijke tools is The PDF Zone.

Bestanden voorbereiden voor Acrobat

Dus, met het uiteindelijke bestandsformaat beslist, en de tools om dat formaat te maken in de hand, is het tijd om ons bezig te houden met de opmaak van het document.

Op het eerste gezicht lijkt het betrekkelijk eenvoudig: beperk uw ontwerpen en lay-outs tot een gebied dat beide formaten kunnen bevatten.

Als u een A4- en Letter-papier op elkaar legt, met de linkerbovenhoeken tegen elkaar aan, is het verschil tussen de twee vellen duidelijk: Letter is breder dan A4; A4 is langer dan Letter. Wil een ontwerp of lay-out dus veilig op beide bladen passen, dan mag het niet breder zijn dan A4 en niet langer dan Letter. Met andere woorden, de grenzen voor een ontwerp of lay-out die veilig op beide paginaformaten past, zijn de breedte van een A4-vel (210 mm of 8,27˝) en de lengte van een Letter-vel (11˝ of 279,4 mm). Helaas is het niet zo eenvoudig.

Neem één A4-vel, en pas de standaard marges van 25 mm (ongeveer 1˝) toe die de meesten van ons gebruiken bij het voorbereiden van brieven, rapporten, artikelen en dergelijke. Het werkgebied – 160 mm bij 247 mm – valt ruim binnen de hierboven genoemde grenzen. Vul je de pagina echter met tekst, dan ontstaat er een probleem als het document wordt verzonden naar iemand die Letter gebruikt.

De tekst past nog steeds op een enkel US Letter vel, maar het loopt over de marges. Wanneer een Letter-gebruiker het bestand afdrukt, zal de pagina ofwel niet goed worden afgedrukt (omdat een deel van de tekst in een niet-afdrukbaar deel van het vel is geplaatst) ofwel op een tweede pagina worden afgedrukt. Het tweede resultaat is beter, maar geen van beide is wenselijk en het tweede is hoe dan ook afhankelijk van te veel oncontroleerbare variabelen.

Om dit probleem te voorkomen, is de enige optie voor A4-gebruikers die documenten delen met Letter-gebruikers, hun ondermarges te vergroten tot 45 mm. Dit zorgt ervoor dat de tekst op hun pagina’s niet in de verboden zone komt wanneer ze worden bekeken en afgedrukt door mensen die nog steeds Letter gebruiken. Ook hier geldt:

Als u overschakelt op liggend, zijn het de Letter-gebruikers die de ondermarge moeten aanpassen. Met een standaardmarge van 25 mm aan alle zijden komt een liggende lay-out die er prima uitziet op Letter-papier op A4-papier in de gevarenzone terecht:

Voeg 6 mm extra toe (ongeveer 0.2˝) aan de ondermarge en het probleem is vermeden:

De lay-outs die hierboven in het klein zijn weergegeven, zijn opzettelijk eenvoudig, maar de voorgestelde margeveranderingen zouden zelfs moeten werken met meer gecompliceerde op raster gebaseerde lay-outs. Er kunnen en zullen echter problemen ontstaan met lay-outs die rond een centrale as zijn opgebouwd in plaats van rond een van de traditionele rasters.

Een lay-out die slechts rond één centrale as is opgebouwd, zou nog steeds acceptabel moeten worden weergegeven en afgedrukt over het gehele papierformaat met de juiste marge-aanpassingen. Een eenvoudige poster in Victoriaanse stijl bijvoorbeeld, opgesteld langs de verticale as in staande weergave:

Als je goed kijkt, zie je één klein probleempje met de weergave. Het ontwerp is perfect gecentreerd op het A4-vel, maar een beetje uit het midden op het US letter-vel. Een onvermijdelijk gevolg van twee dingen: 1) A4 en US Letter zijn niet even breed en 2) bijna elk hulpmiddel om gegevens digitaal op te maken en te presenteren gebruikt de linkerbovenhoek van de pagina als referentiepunt om te bepalen waar objecten op de pagina moeten verschijnen.

Dergelijke problemen zullen zich voordoen bij ontwerpen die rond de verticale as zijn opgebouwd in liggende modus. Als zelfs deze kleine visuele fouten onaanvaardbaar zijn, is er weinig andere keuze dan twee versies van een ontwerp te maken (b.v. een US Letter en A4 versie of een US Tabloid en A3 versie). Ontwerpen die rond zowel de verticale als de horizontale centrale as zijn gebouwd zullen vrijwel zeker zowel US als niet US versies nodig hebben.

Het probleem vermijden om mee te beginnen

Als dit allemaal problemen lijken waar je goed zonder zou kunnen, welkom bij de club. Helaas zijn de enige huidige alternatieven voor het erkennen en aanpakken van het probleem:

1. het negeren ervan en het irriteren en/of verliezen van de gewoonte van mensen die een andere paginagrootte gebruiken dan u.

2. de VS (en Canada) ervan overtuigen hun verschillende Imperiale maatsystemen op te geven en volmondig over te stappen op het SI (ofmetrisch, om de minder formele term te gebruiken) systeem.

De meeste mensen zullen het probleem uiteindelijk negeren. Voor mensen die om niet-commerciële redenen documenten delen, is dit niet meer dan een irritante fout in de omgangsvormen, die meestal wordt vergeven of in ieder geval niet wordt opgemerkt door de betrokken partij.

En ondanks de omvang is het een veelgemaakte commerciële fout, omdat de verloren omzet wordt verborgen door de relatieve omvang van de twee betrokken grote economieën: de VS en de EU. Iemand die succesvol opereert in de ene sfeer kan de andere negeren en de verloren inkomsten niet opmerken.

Wat betreft het tweede alternatief, en ondanks mijn gedempte optimisme hierboven, zie ik het niet gebeuren in de nabije toekomst. Een omschakeling per fiat (zoals in 1974 in Australië met succes is gebeurd) is uiterst onwaarschijnlijk en de langzame osmose van metrieke begrippen in het leven in de VS heeft nog niet het stadium bereikt waarin dergelijke maten hun imperiale equivalenten vervangen.

Waardoor we blijven waar we begonnen zijn: omgaan met twee enigszins verschillende papierformaten en alle ongemakken die uit de verschillen voortvloeien.