Halfwaardetijd

Figuur 1. Een grafiek van het verval van een radioactieve kern in de tijd. De tijd die de massa of de activiteit van de bron (het aantal vervalgebeurtenissen per seconde) nodig heeft om tot de 50%-grens te dalen, is de halfwaardetijd. De halfwaardetijd in deze afbeelding is 1 jaar.

De halfwaardetijd is de tijd die nodig is om de helft van de oorspronkelijke waarde van een bepaalde hoeveelheid van een radioactief element te laten vervallen. Daarnaast is een halfwaardetijd de tijd die nodig is voor de activiteit van een bron om te dalen tot de helft van de oorspronkelijke waarde. De tweede wet van de thermodynamica, in het bijzonder de wanordelijkheidsverklaring, kan worden gebruikt om te helpen begrijpen waarom radioactief verval optreedt. Deze wet zegt dat de entropie van een gesloten systeem nooit kan afnemen, wat betekent dat dingen verder in wanorde moeten vervallen, niet in orde. Dit proces staat bekend als “verval” en de tweede wet helpt te verduidelijken waarom materie in de loop van de tijd afbreekt tot een steeds minder georganiseerde toestand. Een deel van dit proces omvat bepaalde soorten atomen die afbreken in nieuwe, andere soorten atomen met een meetbare snelheid die bekend staat als radioactief verval.

Alle radioactieve materialen hebben instabiele kernen in zich. Daarnaast zijn er ook enkele kernen in de stof die zich al in hun stabiele toestand bevinden, maar de verhouding tussen stabiele en onstabiele kernen in een monster kan variëren. De stabiele kernen in het monster zijn onveranderlijk (en in een stabiele energetische toestand), maar de onstabiele kernen zullen na verloop van tijd een soort nucleair verval ondergaan om stabiel te worden. Dit resulteert in een emissie van een of andere vorm van straling. Aangezien de halfwaardetijd een maat voor de tijd is, is de halfwaardetijd een waarde die bepaalt hoe lang deze reductie tot een stabielere energietoestand zal duren.

Verschillende stoffen ondergaan een sneller verlies van hun radioactiviteit dan andere. Bij sommige radioactieve elementen kan de helft van hun onstabiele kernen in minder dan één seconde vervallen. Zo heeft krypton-101 een halveringstijd van ongeveer een tienmiljoenste van een seconde. Sommige elementen daarentegen hebben een buitengewoon lange halveringstijd en doen er miljarden jaren over om te vervallen. Uranium-238 heeft een halveringstijd van 4,51 miljard jaar. Dit betekent dat het miljarden jaren zou duren voordat uranium-238 vervalt in een verhouding van half uranium-238 en half thorium-234. Uranium-235 (een andere natuurlijk voorkomende isotoop van uranium) heeft een kortere halfwaardetijd dan uranium-238, namelijk slechts ~700 miljoen jaar.

Vergelijking

Er is een vergelijking die vaak wordt gebruikt om te bepalen hoeveel er van een bepaalde radioactieve stof overblijft nadat een bepaalde tijd is verstreken. Dit wordt bepaald aan de hand van eigenschappen als de halveringstijd van de stof en hoeveel er aanvankelijk van de stof over was. De gebruikte vergelijking is:

waar:

• de hoeveelheid stof is nadat de tijd is verstreken
• de aanvankelijke hoeveelheid stof is
• de hoeveelheid tijd die is verstreken
• de halfwaardetijd van de stof is

Een soortgelijke vergelijking kan ook worden gebruikt om aan te tonen hoe de activiteit van de stof in de loop van de tijd afneemt. Wanneer dit wordt uitgedrukt, heeft de vergelijking de vorm:

waar:

• de activiteit van de stof is nadat de tijd is verstreken
• de aanvankelijke activiteit van de stof is
• de hoeveelheid tijd die is verstreken
• de halfwaardetijd van de stof

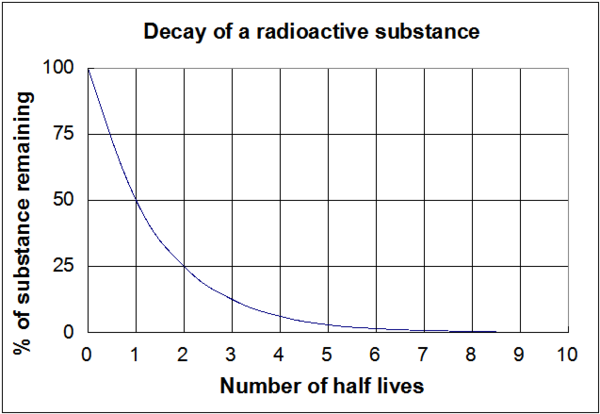
De in figuur 1 weergegeven grafiek is een visuele weergave van deze bovenstaande vergelijkingen. Het is belangrijk op te merken dat ongeacht de werkelijke lengte van het halfwaardetijd (of het nu miljoenen jaren of een paar nanoseconden is) de vorm van de grafiek hetzelfde zal zijn.

De kennis van halfwaardetijden is een onderdeel van hoe geologen gesteenten dateren met radio-isotopische datering.