Logistische regressie

Logistische regressie (ook wel logit regressie of logit model genoemd) werd ontwikkeld door de statisticus David Cox in 1958 en is een regressiemodel waarbij de responsvariabele Y categorisch is. Logistische regressie maakt het mogelijk de waarschijnlijkheid van een categorische respons te schatten op basis van een of meer voorspellende variabelen (X). Men kan zeggen dat de aanwezigheid van een voorspeller de kans op een bepaalde uitkomst met een bepaald percentage verhoogt (of verlaagt). Deze handleiding behandelt het geval waarin Y binair is – d.w.z. dat hij slechts twee waarden kan aannemen, “0” en “1”, die uitkomsten vertegenwoordigen zoals slagen/niet-slagen, winnen/verliezen, leven/dood of gezond/ziek. Gevallen waarin de afhankelijke variabele meer dan twee uitkomstcategorieën heeft, kunnen worden geanalyseerd met multinomiale logistische regressie, of, indien de meervoudige categorieën geordend zijn, met ordinale logistische regressie. Discriminantanalyse is echter een populaire methode geworden voor classificatie in meerdere klassen, dus onze volgende tutorial zal zich richten op die techniek voor die gevallen.

tl;dr

Deze tutorial dient als een inleiding tot logistische regressie en behandelt1:

1. Replicatievereisten: Wat je nodig hebt om de analyse in deze tutorial te reproduceren
2. Waarom logistische regressie: Waarom logistische regressie gebruiken?
3. Onze gegevens voorbereiden: Onze gegevens voorbereiden voor modellering
4. Eenvoudige logistische regressie: Voorspellen van de kans op respons Y met een enkele voorspellende variabele X
5. Meervoudige logistische regressie: Voorspellen van de kans op respons Y met meerdere voorspellende variabelen
6. Model evaluatie & diagnostiek: Hoe goed past het model bij de gegevens? Welke voorspellers zijn het belangrijkst? Zijn de voorspellingen accuraat?

Replicatievereisten

Deze tutorial maakt voornamelijk gebruik van de Default gegevens die door het ISLR pakket worden geleverd. Dit is een gesimuleerde dataset met informatie over tienduizend klanten, zoals of de klant in gebreke is gebleven, student is, het gemiddelde saldo dat de klant heeft en het inkomen van de klant. We zullen ook een paar pakketten gebruiken die gegevensmanipulatie, visualisatie, functies voor pijplijnmodellering en functies voor het opruimen van modeluitvoer bieden.

# Packageslibrary(tidyverse) # data manipulation and visualizationlibrary(modelr) # provides easy pipeline modeling functionslibrary(broom) # helps to tidy up model outputs# Load data (default <- as_tibble(ISLR::Default))## # A tibble: 10,000 × 4## default student balance income## <fctr> <fctr> <dbl> <dbl>## 1 No No 729.5265 44361.625## 2 No Yes 817.1804 12106.135## 3 No No 1073.5492 31767.139## 4 No No 529.2506 35704.494## 5 No No 785.6559 38463.496## 6 No Yes 919.5885 7491.559## 7 No No 825.5133 24905.227## 8 No Yes 808.6675 17600.451## 9 No No 1161.0579 37468.529## 10 No No 0.0000 29275.268## # ... with 9,990 more rows

Waarom logistische regressie

Lineaire regressie is niet geschikt in het geval van een kwalitatieve respons. Waarom niet? Stel dat we de medische toestand van een patiënte op de spoedeisende hulp proberen te voorspellen op basis van haar symptomen. In dit vereenvoudigde voorbeeld zijn er drie mogelijke diagnoses: beroerte, overdosis drugs en epileptische aanval. We zouden kunnen overwegen deze waarden als volgt te coderen als een kwantitatieve responsvariabele, Y:

Met deze codering zou met behulp van kleinste kwadraten een lineair regressiemodel kunnen worden toegepast om Y te voorspellen op basis van een reeks voorspellers . Helaas impliceert deze codering een rangschikking van de uitkomsten, waarbij overdosis drugs wordt geplaatst tussen beroerte en epileptische aanval, en erop wordt aangedrongen dat het verschil tussen beroerte en overdosis drugs hetzelfde is als het verschil tussen overdosis drugs en epileptische aanval. In de praktijk is er geen bijzondere reden waarom dit het geval zou moeten zijn. Men zou bijvoorbeeld een even redelijke codering kunnen kiezen,

, die een totaal ander verband tussen de drie aandoeningen zou impliceren. Elk van deze coderingen zou fundamenteel verschillende lineaire modellen opleveren die uiteindelijk zouden leiden tot verschillende reeksen voorspellingen over testwaarnemingen.

Meer relevant voor onze gegevens: als wij een klant op basis van zijn saldo als wanbetaler met hoog of laag risico willen classificeren, zouden wij lineaire regressie kunnen gebruiken; de linker figuur hieronder illustreert echter hoe lineaire regressie de waarschijnlijkheid van wanbetaling zou voorspellen. Helaas voorspellen we voor saldi dicht bij nul een negatieve kans op wanbetaling; als we voor zeer grote saldi zouden voorspellen, zouden we waarden krijgen groter dan 1. Deze voorspellingen zijn niet zinvol, aangezien de werkelijke kans op wanbetaling, ongeacht het saldo van de kredietkaart, uiteraard tussen 0 en 1 moet liggen.

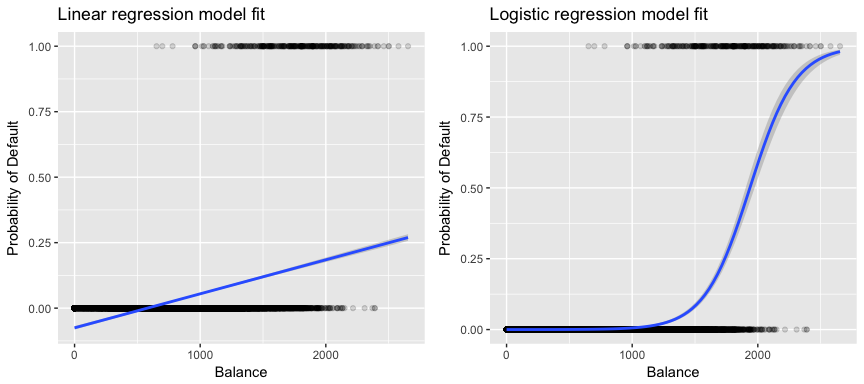
Om dit probleem te vermijden, moeten we p(X) modelleren met behulp van een functie die voor alle waarden van X uitkomsten tussen 0 en 1 geeft. Bij logistische regressie gebruiken we de logistische functie, die is gedefinieerd in Eq. 1 en is afgebeeld in de rechter figuur hierboven.

Voorbereiding van onze gegevens

Zoals in de regressie-tutorial zullen we onze gegevens splitsen in een training- (60%) en test- (40%) dataset, zodat we kunnen beoordelen hoe goed ons model presteert op een out-of-sample dataset.

set.seed(123)sample <- sample(c(TRUE, FALSE), nrow(default), replace = T, prob = c(0.6,0.4))train <- defaulttest <- default

Eenvoudige logistische regressie

We passen een logistisch regressiemodel toe om de kans te voorspellen dat een klant in gebreke blijft op basis van het gemiddelde saldo dat de klant bij zich draagt. De functie glm past gegeneraliseerde lineaire modellen toe, een klasse van modellen die logistische regressie omvat. De syntaxis van de glm-functie is vergelijkbaar met die van lm, behalve dat we het argument family = binomial moeten doorgeven om R te vertellen een logistische regressie uit te voeren in plaats van een ander type gegeneraliseerd lineair model.

model1 <- glm(default ~ balance, family = "binomial", data = train)

Op de achtergrond gebruikt de glm maximale waarschijnlijkheid om het model te passen. De basisintuïtie achter het gebruik van maximale waarschijnlijkheid voor het passen van een logistisch regressiemodel is als volgt: wij zoeken naar ramingen voor en zodanig dat de voorspelde kans op wanbetaling voor elk individu, met gebruikmaking van Eq. 1, zo goed mogelijk overeenstemt met de waargenomen wanbetalingsstatus van het individu. Met andere woorden, wij trachten en zodanig te vinden dat het inbrengen van deze ramingen in het model voor p(X), gegeven in Eq. 1, een getal oplevert dat dicht bij één ligt voor alle individuen die in gebreke bleven, en een getal dicht bij nul voor alle individuen die dat niet deden. Deze intuïtie kan worden geformaliseerd met behulp van een wiskundige vergelijking die waarschijnlijkheidsfunctie wordt genoemd:

De schattingen en worden zo gekozen dat deze waarschijnlijkheidsfunctie wordt gemaximaliseerd. Maximale waarschijnlijkheid is een zeer algemene benadering die wordt gebruikt om veel van de niet-lineaire modellen die we in toekomstige tutorials zullen onderzoeken, in te passen. Het resultaat is een S-vormige waarschijnlijkheidscurve die hieronder wordt geïllustreerd (merk op dat we onze responsvariabele moeten omzetten in een binaire gecodeerde variabele om de logistische regressiefasplijn te kunnen plotten).

default %>% mutate(prob = ifelse(default == "Yes", 1, 0)) %>% ggplot(aes(balance, prob)) + geom_point(alpha = .15) + geom_smooth(method = "glm", method.args = list(family = "binomial")) + ggtitle("Logistic regression model fit") + xlab("Balance") + ylab("Probability of Default")

Zoals bij lineaire regressie kunnen we het model beoordelen met summary of glance. Merk op dat het formaat van de coëfficiëntuitvoer gelijk is aan dat van de lineaire regressie; de goodness-of-fit details onderaan summary verschillen echter. We zullen hier later dieper op ingaan, maar merk alleen op dat u het woord deviantie ziet. Deviantie is analoog aan de som van de kwadraten bij lineaire regressie en is een maat voor het gebrek aan fit met de gegevens in een logistisch regressiemodel. De nuldeviantie vertegenwoordigt het verschil tussen een model met alleen het intercept (wat betekent “geen voorspellers”) en een verzadigd model (een model met een theoretisch perfecte fit). Het doel is dat de modelafwijking (genoteerd als Residuele afwijking) lager is; kleinere waarden wijzen op een betere fit. In dit opzicht biedt het nulmodel een basislijn waarop voorspellende modellen kunnen worden vergeleken.

summary(model1)## ## Call:## glm(formula = default ~ balance, family = "binomial", data = train)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.2905 -0.1395 -0.0528 -0.0189 3.3346 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.101e+01 4.887e-01 -22.52 <2e-16 ***## balance 5.669e-03 2.949e-04 19.22 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 1723.03 on 6046 degrees of freedom## Residual deviance: 908.69 on 6045 degrees of freedom## AIC: 912.69## ## Number of Fisher Scoring iterations: 8

Beoordeling van coëfficiënten

De onderstaande tabel toont de coëfficiëntschattingen en gerelateerde informatie die het resultaat zijn van het fitten van een logistisch regressiemodel om de kans op default = Ja met behulp van saldo te voorspellen. Bedenk dat de coëfficiëntschattingen van logistische regressie de relatie tussen de voorspellende en de responsvariabele karakteriseren op een log-odds schaal (zie Hoofdstuk 3 van ISLR1 voor meer details). Dit wijst erop dat een toename van het saldo gepaard gaat met een toename van de kans op wanbetaling. Om precies te zijn: een toename van het saldo met één eenheid gaat gepaard met een toename van de kans op wanbetaling met 0,0057 eenheden.

tidy(model1)## term estimate std.error statistic p.value## 1 (Intercept) -11.006277528 0.488739437 -22.51972 2.660162e-112## 2 balance 0.005668817 0.000294946 19.21985 2.525157e-82

We kunnen de saldo-coëfficiënt verder interpreteren als – voor elke dollar toename van het maandelijkse saldo neemt de kans dat de klant in gebreke blijft met een factor 1 toe.0057.

exp(coef(model1))## (Intercept) balance ## 1.659718e-05 1.005685e+00

Vele aspecten van de coëfficiëntoutput zijn vergelijkbaar met die besproken in de lineaire regressieoutput. Zo kunnen wij bijvoorbeeld de betrouwbaarheidsintervallen en de nauwkeurigheid van de coëfficiëntschattingen meten door hun standaardfouten te berekenen. Bijvoorbeeld, heeft een p-waarde < 2e-16 wat wijst op een statistisch significante relatie tussen het aangehouden saldo en de kans op wanbetaling. We kunnen de standaardfouten ook gebruiken om betrouwbaarheidsintervallen te krijgen, zoals we in de tutorial over lineaire regressie hebben gedaan:

confint(model1)## 2.5 % 97.5 %## (Intercept) -12.007610373 -10.089360652## balance 0.005111835 0.006269411

Voorspellingen doen

Zodra de coëfficiënten zijn geschat, is het een eenvoudige zaak om de kans op wanbetaling voor een gegeven saldo op de creditcard te berekenen. Wiskundig voorspellen we met behulp van de coëfficiëntschattingen van ons model dat de kans op wanbetaling voor een individu met een saldo van $1.000 minder dan 0,5% bedraagt

We kunnen de kans op wanbetaling in R voorspellen met behulp van de functie predict (zorg ervoor dat u type = "response" opneemt). Hier vergelijken we de kans op wanbetaling op basis van saldi van $1000 en $2000. Zoals u kunt zien, stijgt de kans op wanbetaling aanzienlijk naarmate het saldo van $1000 naar $2000 stijgt, van 0,5% tot 58%!

predict(model1, data.frame(balance = c(1000, 2000)), type = "response")## 1 2 ## 0.004785057 0.582089269

Met het logistische regressiemodel kan men ook kwalitatieve voorspellers gebruiken. Als voorbeeld kunnen we een model fitten dat gebruikmaakt van de variabele student.

model2 <- glm(default ~ student, family = "binomial", data = train)tidy(model2)## term estimate std.error statistic p.value## 1 (Intercept) -3.5534091 0.09336545 -38.05914 0.000000000## 2 studentYes 0.4413379 0.14927208 2.95660 0.003110511

De coëfficiënt die samenhangt met student = Yes is positief, en de bijbehorende p-waarde is statistisch significant. Dit wijst erop dat studenten een hogere kans op wanbetaling hebben dan niet-studenten. In feite suggereert dit model dat een student bijna dubbel zoveel kans heeft om in gebreke te blijven dan niet-studenten. In de volgende paragraaf zullen we echter zien waarom.

predict(model2, data.frame(student = factor(c("Yes", "No"))), type = "response")## 1 2 ## 0.04261206 0.02783019

Multiple Logistic Regression

Wij kunnen ons model, zoals te zien in Eq. 1, zodat we een binaire respons kunnen voorspellen met behulp van meervoudige voorspellers waarbij p voorspellers zijn:

Laten we nu eens een model toepassen dat de kans op wanbetaling voorspelt op basis van de variabelen saldo, inkomen (in duizenden dollars) en studentenstatus. Er is een verrassend resultaat hier. De p-waarden voor saldo en student=Ja-status zijn zeer klein, wat erop wijst dat elk van deze variabelen geassocieerd is met de kans op wanbetaling. De coëfficiënt voor de variabele student is echter negatief, wat erop wijst dat studenten minder kans maken op wanbetaling dan niet-studenten. De coëfficiënt voor de variabele student in model 2, waar we de kans op wanbetaling alleen op basis van de studentenstatus voorspelden, gaf daarentegen aan dat studenten een grotere kans op wanbetaling hebben. Wat geeft dit?

model3 <- glm(default ~ balance + income + student, family = "binomial", data = train)tidy(model3)## term estimate std.error statistic p.value## 1 (Intercept) -1.090704e+01 6.480739e-01 -16.8299277 1.472817e-63## 2 balance 5.907134e-03 3.102425e-04 19.0403764 7.895817e-81## 3 income -5.012701e-06 1.078617e-05 -0.4647343 6.421217e-01## 4 studentYes -8.094789e-01 3.133150e-01 -2.5835947 9.777661e-03

Het rechterpaneel van onderstaande figuur geeft een verklaring voor deze discrepantie. De variabelen student en saldo zijn gecorreleerd. Studenten hebben de neiging een hogere schuld te hebben, wat op zijn beurt gepaard gaat met een grotere kans op wanbetaling. Met andere woorden, studenten hebben vaker een groot saldo op hun creditcard, dat, zoals we weten uit het linkerpaneel van de onderstaande figuur, doorgaans gepaard gaat met een hoge wanbetalingsfrequentie. Hoewel een individuele student met een bepaald kredietsaldo dus een lagere kans op wanbetaling heeft dan een niet-student met hetzelfde kredietsaldo, betekent het feit dat studenten over het algemeen hogere kredietsaldo’s hebben dat studenten over het algemeen een hoger wanbetalingspercentage hebben dan niet-studenten. Dit is een belangrijk onderscheid voor een kredietkaartmaatschappij die probeert te bepalen aan wie zij krediet moet aanbieden. Een student is risicovoller dan een niet-student als er geen informatie over het saldo op de creditcard van de student beschikbaar is. Maar die student is minder riskant dan een niet-student met hetzelfde saldo op zijn creditcard!

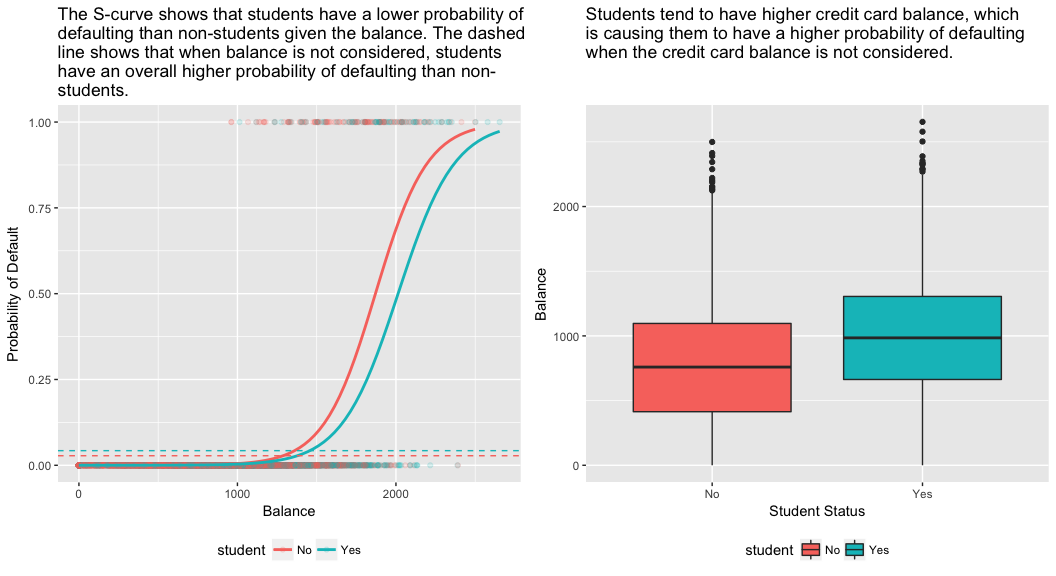
Dit eenvoudige voorbeeld illustreert de gevaren en subtiliteiten die kleven aan het uitvoeren van regressies met slechts één voorspeller, terwijl ook andere voorspellers relevant kunnen zijn. De resultaten die met één voorspeller worden verkregen, kunnen heel anders zijn dan die welke met meerdere voorspellers worden verkregen, vooral wanneer er correlatie tussen de voorspellers bestaat. Dit verschijnsel staat bekend als confounding.

In het geval van meerdere predictorvariabelen willen wij soms begrijpen welke variabele de meeste invloed heeft op het voorspellen van de responsvariabele (Y). We kunnen dit doen met varImp uit het pakket caret. Hier zien we dat saldo met een grote marge het belangrijkst is, terwijl studentenstatus minder belangrijk is, gevolgd door inkomen (dat toch al niet significant bleek te zijn (p = .64)).

caret::varImp(model3)## Overall## balance 19.0403764## income 0.4647343## studentYes 2.5835947

Zoals voorheen kunnen we met dit model gemakkelijk voorspellingen doen. Bijvoorbeeld, een student met een kredietkaart saldo van $1.500 en een inkomen van $40.000 heeft een geschatte kans op wanbetaling van

Een niet-student met hetzelfde saldo en inkomen heeft een geschatte kans op wanbetaling van

new.df <- tibble(balance = 1500, income = 40, student = c("Yes", "No"))predict(model3, new.df, type = "response")## 1 2 ## 0.05437124 0.11440288

Dus zien we dat voor het gegeven saldo en inkomen (hoewel inkomen niet significant is) een student ongeveer de helft minder kans heeft op wanbetaling dan een niet-student.

Modelevaluatie & Diagnostiek

Tot dusver zijn drie logistische regressiemodellen gebouwd en zijn de coëfficiënten onderzocht. Er blijven echter nog enkele kritische vragen over. Zijn de modellen goed? Hoe goed past het model bij de gegevens? En hoe nauwkeurig zijn de voorspellingen bij een out-of-sample dataset?

Goodness-of-Fit

In de lineaire regressie-tutorial hebben we gezien hoe de F-statistiek, en de gecorrigeerde , en residuele diagnostiek ons informeren over hoe goed het model bij de gegevens past. Hier bekijken we een paar manieren om de goodness-of-fit van onze logit-modellen te beoordelen.

Likelihood Ratio Test

Eerst kunnen we een Likelihood Ratio Test gebruiken om te beoordelen of onze modellen de fit verbeteren. Het toevoegen van voorspellende variabelen aan een model zal bijna altijd de model fit verbeteren (d.w.z. de log likelihood verhogen en de model deviantie verminderen ten opzichte van de null deviantie), maar het is noodzakelijk om te testen of het waargenomen verschil in model fit statistisch significant is. We kunnen anova gebruiken om deze test uit te voeren. De resultaten geven aan dat, vergeleken met model1, model3 de residuele deviantie met meer dan 13 vermindert (vergeet niet dat het doel van logistische regressie is een model te vinden dat de deviantie-residuen tot een minimum beperkt). Belangrijker nog, deze verbetering is statistisch significant bij p = 0.001. Dit suggereert dat model3 inderdaad een verbeterde model fit geeft.

anova(model1, model3, test = "Chisq")## Analysis of Deviance Table## ## Model 1: default ~ balance## Model 2: default ~ balance + income + student## Resid. Df Resid. Dev Df Deviance Pr(>Chi) ## 1 6045 908.69 ## 2 6043 895.02 2 13.668 0.001076 **## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pseudo

In tegenstelling tot lineaire regressie met gewone kleinste kwadraten-schatting is er geen statistiek die verklaart welk deel van de variantie in de afhankelijke variabele wordt verklaard door de voorspellers. Er zijn echter een aantal pseudo-metrieken die van waarde kunnen zijn. De meest opvallende is McFadden’s , die gedefinieerd is als

waarbij de logliklikheidswaarde voor het gepaste model en de logliklikiteitswaarde voor het nulmodel met alleen een intercept als voorspeller. De maat varieert van 0 tot iets minder dan 1, waarbij waarden dichter bij nul aangeven dat het model geen voorspellend vermogen heeft. Anders dan bij lineaire regressie halen modellen echter zelden een hoge McFadden . In feite staan modellen met een McFadden pseudo in de woorden van McFadden zelf voor een zeer goede fit. Wij kunnen de pseudowaarden van McFadden voor onze modellen beoordelen met:

list(model1 = pscl::pR2(model1), model2 = pscl::pR2(model2), model3 = pscl::pR2(model3))## $model1## McFadden ## 0.4726215 ## ## $model2## McFadden ## 0.004898314 ## ## $model3## McFadden ## 0.4805543

Wij zien dat model 2 een zeer lage waarde heeft, hetgeen zijn slechte fit bevestigt. De waarden van model 1 en 3 zijn echter veel hoger, wat erop wijst dat zij een behoorlijk deel van de variantie in de standaardgegevens verklaren. Bovendien zien we dat model 3 de fit slechts in zeer geringe mate verbetert.

Residuele beoordeling

Bedenk dat logistische regressie niet veronderstelt dat de residuen normaal verdeeld zijn, noch dat de variantie constant is. Het residu van de deviantie is echter nuttig om te bepalen of individuele punten niet goed door het model worden ingepast. Hier kunnen wij de gestandaardiseerde deviantieresiduen passen om te zien hoeveel er meer dan 3 standaarddeviaties bedragen. Eerst extraheren we met augment enkele nuttige stukjes van de modelresultaten en plotten dan.

model1_data <- augment(model1) %>% mutate(index = 1:n())ggplot(model1_data, aes(index, .std.resid, color = default)) + geom_point(alpha = .5) + geom_ref_line(h = 3)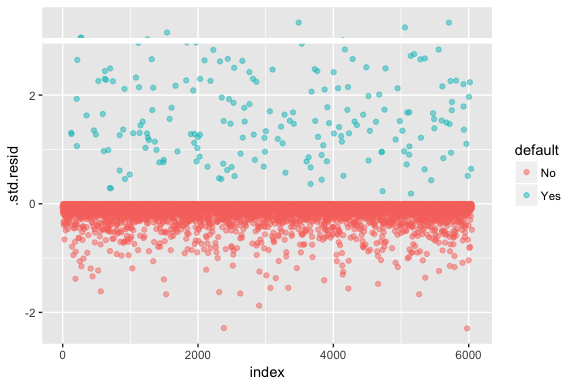

De gestandaardiseerde residuen die groter zijn dan 3 vertegenwoordigen mogelijke uitschieters en verdienen misschien meer aandacht. We kunnen filteren op deze residuen om ze van dichterbij te bekijken. We zien dat al deze waarnemingen klanten vertegenwoordigen die in gebreke bleven met budgetten die veel lager zijn dan de normale wanbetalers.

model1_data %>% filter(abs(.std.resid) > 3)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 Yes 1118.7010 -4.664566 0.1752745 3.057432 0.0002841609 0.3857438 0.01508609 3.057867 271## 2 Yes 1119.0972 -4.662320 0.1751742 3.056704 0.0002844621 0.3857448 0.01506820 3.057139 272## 3 Yes 1135.0473 -4.571902 0.1711544 3.027272 0.0002967274 0.3857832 0.01435943 3.027721 1253## 4 Yes 1066.8841 -4.958307 0.1885550 3.151288 0.0002463229 0.3856189 0.01754100 3.151676 1542## 5 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 6 Yes 1143.6805 -4.522962 0.1689933 3.011233 0.0003034789 0.3858039 0.01398491 3.011690 4142## 7 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 8 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709

Gelijkaardig aan lineaire regressie kunnen we ook invloedrijke waarnemingen identificeren met Cook’s afstandswaarden. Hier identificeren we de top 5 grootste waarden.

plot(model1, which = 4, id.n = 5)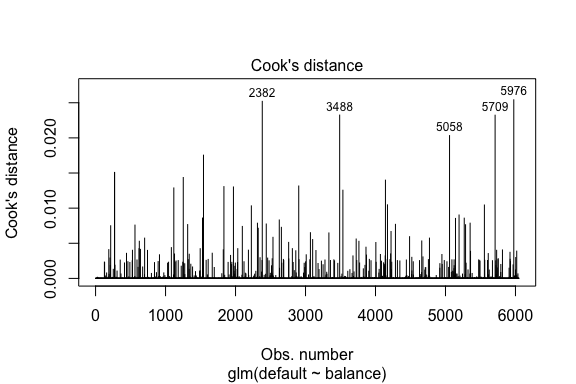

En ook deze kunnen we verder onderzoeken. Hier zien we dat de top vijf invloedrijke punten omvatten:

• klanten die in gebreke bleven met een zeer laag saldo en
• twee klanten die niet in gebreke bleven, maar een saldo van meer dan $ 2.000 hadden

Dit betekent dat als we deze waarnemingen zouden verwijderen (niet aanbevolen), de vorm, locatie en betrouwbaarheidsinterval van onze logistische regressie S-curve waarschijnlijk zou verschuiven.

model1_data %>% top_n(5, .cooksd)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 No 2388.1740 2.531843 0.2413764 -2.284011 0.0039757771 0.3866249 0.02520100 -2.288565 2382## 2 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 3 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 4 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709## 5 No 2391.0077 2.547907 0.2421522 -2.290521 0.0039468742 0.3866185 0.02542145 -2.295054 5976

Validatie van voorspelde waarden

Classificatiegraad

Bij het ontwikkelen van modellen voor voorspelling is de meest kritische maatstaf hoe goed het model het doet bij het voorspellen van de doelvariabele bij waarnemingen buiten de steekproef om. Eerst moeten we de geschatte modellen gebruiken om waarden te voorspellen op onze verzameling van trainingsgegevens (train). Wanneer u predict gebruikt, moet u type = response toevoegen zodat de voorspelling de waarschijnlijkheid van wanbetaling weergeeft.

test.predicted.m1 <- predict(model1, newdata = test, type = "response")test.predicted.m2 <- predict(model2, newdata = test, type = "response")test.predicted.m3 <- predict(model3, newdata = test, type = "response")

Nu kunnen we de voorspelde doelvariabele vergelijken met de waargenomen waarden voor elk model en zien welk model het beste presteert. We kunnen beginnen met gebruik te maken van de verwarringsmatrix, een tabel die de classificatieprestaties voor elk model op de testgegevens beschrijft. Elk kwadrant van de tabel heeft een belangrijke betekenis. In dit geval geven de “Neen” en “Ja” in de rijen aan of klanten in gebreke bleven of niet. De “FALSE” en “TRUE” in de kolommen geven aan of we voorspelden dat klanten in gebreke zouden blijven of niet.

• true positives (kwadrant rechtsonder): dit zijn gevallen waarin we voorspelden dat de klant in gebreke zou blijven en dit ook gebeurde.
• true negatives (kwadrant linksboven): We voorspelden geen wanbetaling, en de klant bleef niet in gebreke.
• valse positieven (kwadrant rechtsboven): We voorspelden ja, maar ze waren niet in gebreke. (Ook bekend als een “Type I fout.”)
• valse negatieven (linksonder): We voorspelden nee, maar ze zijn wel in gebreke gebleven. (Ook bekend als een “Type II fout.”)

De resultaten tonen aan dat model1 en model3 zeer vergelijkbaar zijn. 96% van de voorspelde waarnemingen zijn echte negatieven en ongeveer 1% zijn echte positieven. Beide modellen hebben een type II fout van minder dan 3%, waarbij het model voorspelt dat de klant niet in gebreke blijft, maar dit wel het geval was. En beide modellen hebben een type I-fout van minder dan 1%, waarbij het model voorspelt dat de klant in gebreke zal blijven, maar dat nooit het geval was. model2 De resultaten zijn opmerkelijk verschillend; dit model voorspelt nauwkeurig de niet-defaulters (een gevolg van het feit dat 97% van de gegevens non-defaulters zijn), maar voorspelt nooit de klanten die in gebreke blijven!

list( model1 = table(test$default, test.predicted.m1 > 0.5) %>% prop.table() %>% round(3), model2 = table(test$default, test.predicted.m2 > 0.5) %>% prop.table() %>% round(3), model3 = table(test$default, test.predicted.m3 > 0.5) %>% prop.table() %>% round(3))## $model1## ## FALSE TRUE## No 0.962 0.003## Yes 0.025 0.010## ## $model2## ## FALSE## No 0.965## Yes 0.035## ## $model3## ## FALSE TRUE## No 0.963 0.003## Yes 0.026 0.009

We willen ook inzicht krijgen in de missclassificatiepercentages (ook wel foutenpercentages genoemd) (of we kunnen dit omdraaien voor de nauwkeurigheidspercentages). We zien niet veel verbetering tussen model 1 en 3 en hoewel model 2 een laag foutenpercentage heeft, mag u niet vergeten dat het nooit nauwkeurig klanten voorspelt die daadwerkelijk in gebreke blijven.

test %>% mutate(m1.pred = ifelse(test.predicted.m1 > 0.5, "Yes", "No"), m2.pred = ifelse(test.predicted.m2 > 0.5, "Yes", "No"), m3.pred = ifelse(test.predicted.m3 > 0.5, "Yes", "No")) %>% summarise(m1.error = mean(default != m1.pred), m2.error = mean(default != m2.pred), m3.error = mean(default != m3.pred))## # A tibble: 1 × 3## m1.error m2.error m3.error## <dbl> <dbl> <dbl>## 1 0.02782697 0.03491019 0.02807994

We kunnen een aantal aanvullende inzichten verkrijgen door te kijken naar de ruwe waarden (geen percentages) in onze verwarringsmatrix. Laten we eens kijken naar model 1 ter illustratie. We zien dat er in totaal klanten zijn die in gebreke bleven. Van het totaal aantal wanbetalingen werden er niet voorspeld. Als alternatief kunnen we zeggen dat slechts een deel van de gevallen van wanbetaling werd voorspeld – dit wordt de precisie (ook bekend als gevoeligheid) van ons model genoemd. Dus terwijl het totale foutenpercentage laag is, is het precisiepercentage ook laag, wat niet goed is!

table(test$default, test.predicted.m1 > 0.5)## ## FALSE TRUE## No 3803 12## Yes 98 40

Bij classificatiemodellen zult u ook de termen sensitiviteit en specificiteit tegenkomen wanneer u de prestaties van het model karakteriseert. Zoals hierboven vermeld, is sensitiviteit synoniem met precisie. De specificiteit is echter het percentage niet-defaulters dat correct wordt geïdentificeerd, hier (de nauwkeurigheid wordt hier grotendeels bepaald door het feit dat 97% van de waarnemingen in onze gegevens niet-defaulters zijn). Het belang tussen sensitiviteit en specificiteit is afhankelijk van de context. In dit geval zal een kredietkaartmaatschappij waarschijnlijk meer belang hechten aan sensitiviteit omdat zij haar risico wil beperken. Daarom zullen zij wellicht meer belang hechten aan het afstemmen van een model zodat hun sensitiviteit/precisie wordt verbeterd.

De ontvangende operationele karakteristiek (ROC) is een visuele maatstaf voor de prestaties van de classificator. Met behulp van het percentage positieve datapunten dat correct als positief wordt beschouwd en het percentage negatieve datapunten dat ten onrechte als positief wordt beschouwd, genereren we een grafiek die de afruil laat zien tussen de snelheid waarmee je iets correct kunt voorspellen en de snelheid waarmee je iets foutief voorspelt. Uiteindelijk gaat het om de oppervlakte onder de ROC-curve, of AUC. Die waarde varieert van 0,50 tot 1,00, en waarden boven 0,80 geven aan dat het model goed onderscheid maakt tussen de twee categorieën waaruit onze doelvariabele bestaat. We kunnen de ROC en AUC vergelijken voor model 1 en 2, die een sterk verschil in prestatie te zien geven. We willen beslist dat onze ROC-plots meer lijken op die van model 1 (links) dan op die van model 2 (rechts)!

library(ROCR)par(mfrow=c(1, 2))prediction(test.predicted.m1, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()prediction(test.predicted.m2, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()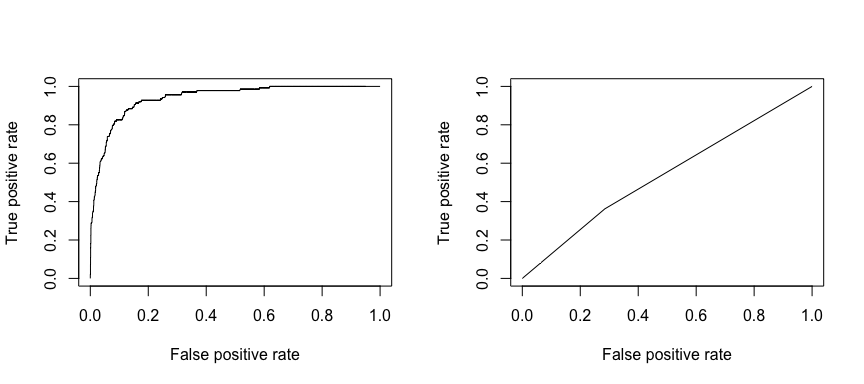

En om de AUC numeriek te berekenen, kunnen we het volgende gebruiken. Vergeet niet dat de AUC varieert van .50 – 1.00. Model 2 is dus een zeer slecht classificerend model, terwijl model 1 een zeer goed classificerend model is.

# model 1 AUCprediction(test.predicted.m1, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.939932# model 2 AUCprediction(test.predicted.m2, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.5386955

We kunnen onze modellen blijven “tunen” om deze classificeringspercentages te verbeteren. Als u uw AUC- en ROC-curven kunt verbeteren (wat betekent dat u de classificatienauwkeurigheidspercentages verbetert), creëert u “lift”, wat betekent dat u de classificatienauwkeurigheid verhoogt.

Aanvullende hulpmiddelen

Hiermee kunt u aan de slag met logistische regressie. Bedenk dat er nog veel meer is om in te verdiepen, dus de volgende bronnen helpen u meer te leren:

• An Introduction to Statistical Learning
• Applied Predictive Modeling
• Elements of Statistical Learning