Oppervlakte van een onregelmatige veelhoek

Dit artikel beschrijft een eenvoudige oplossing voor een meetkundig probleem, een probleem dat ik online op te ingewikkelde manieren beschreven vind. Het probleem is om de oppervlakte en omtreklengte te berekenen van een tweedimensionale, gesloten figuur zoals de plattegrond van een kamer, of een stuk land, of elke andere tweedimensionale begrensde figuur (een “onregelmatige veelhoek”), ongeacht hoe complex.

Ik claim zeker niet originaliteit voor deze methode. Versies bestaan al sinds de tijd van Gauss of daarvoor. Maar de meeste online artikelen beschrijven de methode op onnodig ingewikkelde manieren. Verwijzingen zijn onder meer het Wikipedia artikel over de schoenveterformule, een even ingewikkelde methode in het Polygon artikel, en een aantal artikelen die meer berekend lijken om de eruditie van de auteur aan te tonen dan om de minst ingewikkelde belichaming van de methode te geven. Dit artikel (PDF) toont een van de minst complexe (maar zeker niet eenvoudige) uitdrukkingen:

(1) $A = \frac{1}{2} \x_0 & x_1 y_0 & y_1 einde{array} \rechts + links begin{array}{cc} x_1 & x_2 y_1 & y_2 Einde{array} \rechts + links begin{array}{cc} x_2 & x_3 y_2 & y_3 einde{array} \rechts + … + \begin{array}{cc} x_{n-2} & x_{n-1} \ y_{n-2} & y_{n-1} \eind{array} \rechts| + links|begin{array}{cc} x_{n-1} & x_0 \ y_{n-1} & y_0} \right| \right}$

Waarbij $x_n,y_n$ een hoekpunt van een veelhoek is, uitgedrukt in cartesische coördinaten, en $\left}{array}{cc} x_0 & x_1 \ y_0 & y_1 } \recht$ verwijst naar een determinant, met de waarde $x_0 maal y_1 – y_0 maal x_1$

Wees niet ontmoedigd door de bovenstaande uiteenzetting – het gebruik van deze methode is gemakkelijker dan het begrijpen van de wiskundige onderbouwing. Bij het bestuderen van dit artikel vond ik antwoorden op vragen van leerlingen die zo ingewikkeld waren dat ze de leerling onmogelijk konden inlichten. In dit artikel zal ik er alles aan doen om deze methode zo eenvoudig en toegankelijk mogelijk te maken.

De methode is het eenvoudigst uit te drukken als een algoritme:

• De hoekpunten van een onregelmatige veelhoek kunnen worden voorgesteld als cartesische coördinaten: $x,y$.
• Elk paar coördinaten wordt verwerkt in een algoritme voor oppervlaktetelling dat er als volgt uitziet:
  

  $A = A + \frac{(x_1 \times y_0 – y_1 \times x_0)}{2}$
  $A = A + \frac{(x_2 \times y_1 – y_2 \times x_1)}{2}$
  …

• Een eenvoudige wiskundige uitdrukking voor het bovenstaande zou zijn:
  

  (2) Oppervlakte onregelmatige veelhoek $ \sum_{i=m}^{n-1}{x_{i+1} \tijden y_i – y_{i+1} \x_i}$

• NOOT: In vergelijking (2) eindigt de doorkruiste figuur met het laatste gegeven, het herhaalt niet het begingegeven zoals in vergelijking (1) hierboven. Voor mijn doeleinden, die hieronder worden uitgelegd, is deze vorm opzettelijk – in een landmeting moeten de veldgegevens de figuur afsluiten, d.w.z. het laatste gegeven moet gelijk zijn aan het eerste. In een dergelijke toepassing zou het automatisch sluiten van de figuur zoals in vergelijking (1) fouten verbergen die moeten worden geëvalueerd.

  Gebruikers kunnen de voorkeur geven aan de vorm in vergelijking (1) hierboven, voor andere doeleinden dan de reductie van landmeetkundige gegevens. Voor die doeleinden, tijdens de verwerking gewoon herwaarderen het eerste data-item aan het einde van de traversal, of gegevensreeksen die het eerste data-item te herhalen als de laatste.

• Hier is een complete, werkende Python-functie:
  

  def find_area(array): a = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) ox,oy = x,y return a/2 

• Het “array”-argument hierboven is een verzameling cartesische $x,y$-coördinaten, d.w.z.e. ((10,10),(10,20),(20,20),(20,10),(10,10)). Merk op dat het eerste gegeven aan het eind wordt herhaald.

• Hier volgt een iets complexere Python-functie die zowel oppervlakte als omtreklengte berekent:
  

  def find_area_perim(array): a = 0 p = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) p += abs((x-ox)+(y-oy)*1j) ox,oy = x,y return a/2,p 

• Wederom dit geheugensteuntje: voor beide bovenstaande codevoorbeelden geldt dat in andere toepassingen dan reductie van landmeetkundige gegevens, de verstrekte dataset een kopie van het eerste gegevensitem als laatste moet bevatten, d.w.z.

• Ik heb Python gekozen voor deze voorbeelden omdat een Python listing de algoritmische betekenis maximaliseert en tegelijkertijd de cruft minimaliseert.

• De bovenstaande functies kunnen gemakkelijk worden omgezet in andere talen, bijna direct – behalve de hierboven getoonde perimetertoptelling, die gebruik maakt van het feit dat Python complexe getallen ondersteunt. Voor talen die geen complexe getallen ondersteunen, kan men het omtreksommetje op deze manier maken:

  C/C++: p += sqrt(pow(x-ox,2)+pow(y-oy,2));

  Java: p += Math.sqrt(Math.pow(x-ox,2)+Math.pow(y-oy,2));

• Vormelijk is de omtreklengte de som van de vectormagnitudes:
  

  (3) Omtreklengte $Displaystyle P = \sum_{i=m}^{n-1}{\sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2}}$

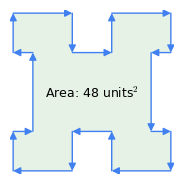
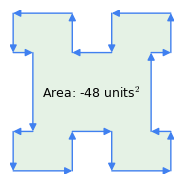Figuur 1: Met de klok mee vs. tegen de klok in vectoren

Hier volgen enkele belangrijke eigenschappen van deze methode:

• Het gekozen beginpunt binnen de veelhoek is niet van belang voor de berekening van oppervlakte of omtrek, alleen dat de figuur gesloten is, d.w.z.Dat wil zeggen dat de laatste coördinaat gelijk moet zijn aan de eerste.
• Regel met de wijzers van de klok mee: de volgorde van de vectoren is belangrijk – als de omtrek met de wijzers van de klok mee wordt doorlopen, is het resultaat positief, als het tegen de wijzers van de klok in wordt doorlopen, is het negatief (figuur 1). Het is deze eigenschap van de methode die de oppervlakte van verbuigingen aftrekt van een complexe figuur zoals in figuur 1 – de “verbuigingen” vertegenwoordigen een linksdraaiende omtrek binnen de veelhoek.
• Vele toepassingen van deze methode gebruiken oorspronkelijke gegevensbronnen bestaande uit polaire vectoren (een voorbeeld zijn de wettelijke beschrijvingen van landmetingen), maar deze methode vereist cartesische coördinaten. De conversie van polaire naar cartesiaanse coördinaten is triviaal, maar het is belangrijk om deze vereiste in gedachten te houden.
• Ook hier geldt dat voor een nauwkeurige oppervlakteberekening, de beschreven veelhoek een gesloten figuur moet zijn – de laatste coördinaat moet gelijk zijn aan de eerste. Voor toepassingen die gebruik maken van veldgegevens bestaande uit lengtevectoren die vervolgens worden omgezet in cartesiaanse vorm, is het een goed idee om de begin- en eindcoordinaten in cartesiaanse vorm te vergelijken – ze moeten gelijk zijn. Bijvoorbeeld, oudere landmetingen (voor het tijdperk van goedkope computerkracht) falen regelmatig voor deze test.

Dit gedeelte is een volledig functionele area/perimeter computer die ingevoerde Cartesische of polaire coördinaat gegevensparen, of landmeetkundige wettelijke beschrijvingen kan verwerken. U hoeft alleen maar een gegevenstype te kiezen (cartesische x,y-coördinaten, polaire m,θ-coördinaten of een landmeetkundige juridische beschrijving) en gegevens in te voeren (of te plakken) in het onderstaande gegevensinvoerveld. U kunt ook voorbeelddatasets selecteren om ermee vertrouwd te raken en te oefenen.

Omwille van browserveiligheidskwesties, om overmatig typewerk te vermijden en om aanzienlijke hoeveelheden gegevens uit een andere bron te importeren, zullen lezers hun systeemklembord moeten gebruiken. Kopieer gewoon gegevens naar het klembord in de bronapplicatie, klik dan op het gegevensinvoerveld eronder en druk op Crtl+A om alles te selecteren, Ctrl+V om gegevens van elders te kopiëren, en Ctrl+C om uw eigen ingevoerde gegevens te kopiëren. De meeste browsers hebben ook klembordfuncties als menu-items.

Kies het type gegevens:

Cartesisch (x,y)

polair (m,θ)

Onderzoeksbeschrijving

Gegevensinvoergebied: Alles selecteren: Ctrl+A | Kopiëren: Ctrl+C | Plakken: Ctrl+V

Grafiek gebied:

Sorry – uw browser ondersteunt de grafische mogelijkheden niet die deze functie vereist –
overweeg Google Chrome of Firefox te installeren.

Opties:

Lijnen

Pijlen

Oorsprong

Centrum

Lengte Eenheid:

Lijnbreedte:

Omgekeerd

Resultaten:Alles selecteren: Ctrl+A | Kopiëren: Ctrl+C | Plakken: Ctrl+V

De oppervlakte/perimeter computer heeft drie invoer modes:

• Cartesische (x,y) coördinaten paren:

  • Elke coördinaat is een tweedimensionale positie met een horizontaal (x) en verticaal (y) deel (een cartesische coördinaat).
  • De coördinaten zijn niet cumulatief – elk beschrijft onafhankelijk zijn locatie.
  • Dus een vierkant zou zijn:
    • 0,0 (oorsprong)
    • 0,100 (omhoog)
    • 100,100 (rechts)
    • 100,0 (omlaag)
    • 0,0 (terug naar de oorsprong)
  

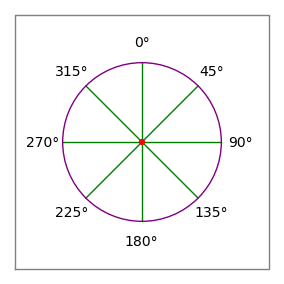  Figuur 2: Kompasroos

  • De komma’s in bovenstaand voorbeeld zijn alleen bedoeld om de gegevensparen te groeperen voor de lezer – zij hebben geen betekenis voor de gegevensparser van de gebiedscomputer.
  • De parser is robuust genoeg dat het bovenstaande voorbeeld in het data-entry gebied van de computer kan worden geplakt en het zal werken (probeer het).
  • De enige beperking is dat verklarende opmerkingen geen getallen kunnen bevatten.

• Polaire (m,θ) coördinatenparen:

  • Elke coördinaat bestaat uit een afstand en een hoek in graden (een polaire vector).
  • De hoeken volgen de kompasconventie – 0 graden is naar boven of “noord”, 90 graden is naar rechts of “oost” (figuur 2).
  • In tegenstelling tot de voorafgaande cartesiaanse vorm, zijn deze coördinaten cumulatief – elke nieuwe vector voegt toe aan de huidige positie.
  • Dus een vierkant zou zijn:
    • 100,0 (omhoog)
    • 100,90 (rechts)
    • 100,180 (omlaag)
    • 100,270 (terug naar de oorsprong)
  • Zoals eerder, zal dit voorbeeld werken als het in het data-entry gebied van de computer wordt geplakt en de polaire modus geselecteerd is.
  • Merk bij poolcoördinaten op dat de oorsprong impliciet is en vooraf is ingesteld op x = 0, y = 0.
  

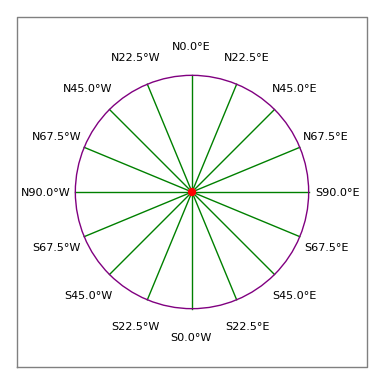  Figuur 3: Landmeterskompasroos

• Wettelijke omschrijving:

  • Eerst een verklaring van het verband tussen de selectie “Lengte-eenheden” en de weergave van de resultaten:
    • Voor elke polygoon wordt een lijst van oppervlakteresultaten berekend met gebruikmaking van een vaste set gemeenschappelijke oppervlakte-eenheden (feet2, meters2, enz.). Om deze oppervlaktelijst zinvol te laten zijn, moeten de ingevoerde lengte-eenheden bekend zijn.
    • In cartesiaanse en polaire modus hebben invoergegevens geen eenheden, dus de gebruiker kiest zelf welke eenheden hij aan de lengtes toekent. Dus wanneer de gebruiker de lengte-eenheden verandert, veranderen de oppervlaktewaarden, de lengte-etiketten veranderen, maar de lengtewaarden niet.
    • In de landmeetkundige modus bevat de wettelijke beschrijving lengte-eenheden (voet, meter, enz.), wat betekent dat de lengte-eenheden vooraf zijn gedefinieerd door de bron. Dus wanneer de gebruiker de lengte-eenheden verandert, verandert dit de lengte-labels en waarden, niet de oppervlakte-waarden.
  • De landmeetkundige beschrijving parser is veruit de minst betrouwbare van de drie data parsing methoden – het is meer een experiment dan een robuuste data conversie methode.
  • Ik schreef deze parser door een aantal wettelijke beschrijvingen te downloaden (die als voorbeelden in de bovenstaande calculator worden gegeven) en de code van de parser af te stellen totdat ze alle met succes konden worden gedecodeerd.

  Criteria voor “succes” waren dat het resultaat hetzelfde vierkante gebied zou hebben als de beschrijving beweert, en dat de figuur “dicht” zou zijn.

  • De term “closure”, en in het bijzonder “error of closure”, wordt bij landmeetkundige werkzaamheden gebruikt om de mate aan te geven waarin het eindpunt van de landmeetkundige doorsnede gelijk is aan het beginpunt. Dit is zelden waar in werkelijkheid – fouten in de sluiting zijn meestal het gevolg van fouten in het veldwerk, en oudere overzichten, gepubliceerd vóór de komst van goedkope computer macht, hebben de neiging om nogal slechte sluitingen hebben, alsmede wild onnauwkeurige schattingen van vierkante oppervlakte.
  • Een landmeetkundige juridische beschrijving is een formele manier om een stuk land te beschrijven – de vorm en syntaxis ervan is in de loop van decennia ontstaan door wederzijds aanvaarde, enigszins arbitraire, conventies die door landmeters worden gedeeld.
  • Voor deze oppervlakte/perimeter-computer moeten de ingevoerde gegevens bepaalde strikte conventies volgen die sommige, maar niet alle, juridische beschrijvingen aanhangen. De essentiële elementen zijn:
    • Het bestaan van de zinsnede “beginpunt”, die een bepaalde voorlopige inhoud scheidt van die welke de afmetingen beschrijft van het perceel dat wordt beschreven. Sommige documenten zeggen “True point of beginning”, sommige zeggen “Real point of beginning” en sommige zeggen “Point of beginning”. Een succesvolle parser moet de inhoud vóór deze zin verwijderen en alles erna behouden.
    • Een reeks zinnen die een speciaal soort polaire vector beschrijven die door landmeters wordt gebruikt:
      • Het woord “Noord” of “Zuid”, of de afkorting “N” of “S”.
      • Dan een hoek uitgedrukt in graden, minuten en seconden.
      • Dan het woord “Oost” of “West”, of de afkorting “E” of “W”.
      • Dan een afstand.
      • Dan een afstandseenheid – voeten, meters, enz.
  • Hier zijn enkele verschillende voorbeelden van landmeter vectoren uit het monster wettelijke omschrijvingen:
    • N 2°0’0″ W – 63.50 feet
    • N90°00’00 “W ALONG A LINE PARALLEL WITH SAID NORT LINE A DISTANCE OF 6.00 FEET
    • North 0°06’O0″ West a distance of 554.86 feet
    • S. 22 degrees 41′ 55″ E. 174.10 feet
  • Merk aan de bovenstaande voorbeelden op dat zij alle een verschillende syntaxis hebben. Er bestaan veel wettelijke beschrijvingen die deze parser niet met succes zal decoderen, alleen omdat ik niet geprobeerd heb hun syntaxis over te nemen. Maar het is belangrijk om toe te voegen dat een echt robuuste parser voor de veelheid van wettelijke beschrijvingen in het bestaan zou moeten zijn zo slim als Watson.
  • Gebruikers van deze gebied/perimeter computer kunnen willen voorkomen dat het indienen van plain-text wettelijke beschrijvingen en hopen dat de parser zal uitzoeken. Om directe handinvoer te maken (of om een lijst van traverses elders te maken voor invoer), gebruik deze conventie:
    • Bedenk dat een aanvaardbare traverse-invoer bestaat uit het woord “Noord” of “Zuid”, of de letter “N” of “S”, gevolgd door maximaal drie getallen die graden, minuten en seconden van de hoek geven, gevolgd door het woord “Oost” of “West” of de letter “E” of “W”, gevolgd door een afstand, gevolgd door een afstandseenheid.
    • Dus een aanvaardbare invoer zou zijn “N 30 15 45 W 100 voet”, hetgeen betekent een traverse van 100 voet wijzend op 30 graden, 15 minuten en 45 seconden ten westen van het noorden (d.w.z. ruwweg 330 kompasgraden, zie figuur 3).
    • De minuten en seconden kunnen worden overgeslagen als ze gelijk zijn aan nul, of als de invoer in decimale graden is, of graden en decimale minuten.
  • Het is niet moeilijk om een gedrukte wettelijke beschrijving om te zetten in dergelijke invoer, en er zijn een aantal manieren om fouten op te sporen. Nadat alle traverses zijn ingevoerd, als de figuur geen sluitingsfout heeft en dezelfde vierkante oppervlakte rapporteert als het origineel, is de kans groot dat de invoer correct is (of ze hebben dezelfde fouten als de oorspronkelijke beschrijving).
  • Na het invoeren van een juridische beschrijving op deze manier, als er een onaanvaardbare sluitingsfout is of de vierkante oppervlakte verkeerd is, bedenk dan dat de oorspronkelijke gegevens verkeerd kunnen zijn. Er zijn een willekeurig aantal wettelijke beschrijvingen in omloop die nooit zijn gecontroleerd met een computer-methode als deze, en die nooit correct waren.

Terwijl u de cartesische (x,y) voorbeelden doorbladert, let dan op de verschillende vormen in verhouding van oppervlakte en omtrek. De “oneven gevormde veelhoek” heeft een tussenliggende verhouding, de cirkel heeft de kleinste verhouding, en de Hilbert ruimte heeft verreweg de grootste verhouding. Deze verhouding strekt zich uit tot hogere dimensies, waar een bol het grootste volume per oppervlakte heeft.

Over het cirkelvoorbeeld – het is een “eenheidscirkel”, een cirkel met een straal van één. Voor het gegeven voorbeeld benadert de oppervlakte $2pi$ en de omtrek $2pi$, de juiste waarden voor een eenheidscirkel. Om die waarden meer dan benaderingen te laten zijn, om precies gelijk te zijn aan $2 en $2, zou het aantal zijden van de veelhoek oneindig moeten zijn. Ik heb besloten dit niet te doen. 🙂

Het Hilbert ruimte voorbeeld is gegenereerd met een Sage algoritme met een bescheiden volgorde keuze (om niet te veel data te genereren). In principe kan een Hilbert-ruimte een oneindige verhouding hebben tussen omtrek en oppervlakte in twee dimensies, of oppervlakte en volume in drie dimensies. Om te zien hoe complex een Hilbert ruimte kan worden, klik hier om een orde-7 Hilbert ruimte te zien.

Merk aan het Hilbert voorbeeld op dat de berekende oppervlakte dicht bij 1/2 ligt voor een 1×1 oppervlakte. Idealiter, zonder de noodzaak om een lijnfiguur om te zetten in een oppervlaktefiguur en met het juiste algoritme, zou de oppervlakte precies 1/2 zijn van die van een vierkant van dezelfde afmetingen.

De poolinvoermodus is min of meer gelijk aan Turtle graphics, als men nul graden vervangt door “omhoog”, 90 graden door “rechts”, enz., en als elke draai en zet-sequentie wordt samengevat in één commando. Het gebruik van de polaire invoermodus is een gemakkelijke manier om een complexe vorm met de hand te construeren, omdat afstanden en hoeken gemakkelijker zijn bij te houden dan cartesiaanse coördinaten.

Ik gebruikte de hierboven beschreven landmeetkundige gebiedsberekeningsmethode voor het eerst jaren geleden, toen ik op het platteland van Oregon woonde, omringd door mensen die de oppervlakte en omtrek van hun eigendommen moesten weten. Ik kwam vele schokkende voorbeelden tegen van makelaars die brutaal mensen bedrogen die geen manier hadden om uit te vinden wat er aan de hand was. Bij een aantal gelegenheden berekende ik een oppervlakte uit een wettelijke beschrijving, alleen om te ontdekken dat de garantie akte de bewering over areaal was wild onnauwkeurig – en altijd hoger dan de werkelijkheid.

Bij een gelegenheid werd ik gevraagd om een onroerend goed te splitsen in twee gelijke delen en juridische beschrijvingen te maken voor elk. Omdat ik een pas aangeschafte Apple II had (die de verwerkingskracht had van een moderne puntenslijper), was dit heel gemakkelijk – maar terwijl ik werkte realiseerde ik me dat het totale areaal ongeveer drie acres, ongeveer 25% van het totaal, niet klopte. Ik confronteerde het titelbedrijf, dat brutaal antwoordde: “Zie hier, waar de akte zegt ‘meer of minder’?”

Bij een andere gelegenheid begon ik met de aankoop van land, maar gewaarschuwd door de bovenstaande ervaring, besloot ik, toen ik het eigendomsbewijs ontving, de juridische beschrijving in mijn programma in te voeren om te zien of de areaalclaim juist was. Maar tot mijn afgrijzen ontdekte ik dat alle eigendomsakten voor de percelen in die sectie dezelfde juridische beschrijving hadden – van het eerste opgemeten eigendom. Het bleek dat de landontwikkelingsmaatschappij had besloten geld te besparen door slechts één van de tientallen te koop aangeboden kavels op te meten en die wettelijke beschrijving in alle eigendomscontracten op te nemen. Ze waren er zeker van dat ze daarmee weg zouden komen – wie weet er immers iets van wiskunde?

Na een discussie met het titelbedrijf en de projectontwikkelaar, in een poging hen ervan te overtuigen te betalen voor landmetingen zodat de wettelijke beschrijvingen geen beleefde ficties waren, gaf ik het op en besloot het land niet te kopen. Het was net als uitvinden hoe worst wordt gemaakt – het is mogelijk om te veel te weten.

• 04.15.2013 Versie 1.3. Gedetailleerde uitleg toegevoegd over het standaard dataformaat, d.w.z. lijsten die het eerste datapunt herhalen als het laatste.
• 03.24.2013 Versie 1.2. Verder geoptimaliseerd de enquête beschrijving parser, meer resultaat data velden toegevoegd.
• 03.23.2013 Versie 1.1. Verbeterd de wettelijke beschrijving parser om te gaan met meer soorten beschrijvingen, toegevoegd lengte-eenheden selector en een resultaat lijst van gebieden in gemeenschappelijke eenheden.
• 03.22.2013 Versie 1.0. Initiële publieke versie.