Rozglądając się w przyrodzie, być może zauważyłeś skomplikowane rośliny, takie jak te:


Ta paproć składa się z wielu małych liści, które odgałęziają się od większego.


Ten brokuł Romanesco składa się z mniejszych conescubesspheres spiralnie wokół większego.
Początkowo wydaje się, że są to bardzo złożone kształty – ale po bliższym przyjrzeniu się, można zauważyć, że oba są zgodne ze stosunkowo prostym wzorem: wszystkie poszczególne części roślin wyglądają dokładnie tak samo jak cała roślina, tylko są mniejsze. Ten sam wzór powtarza się w kółko, w mniejszych skalach.
W matematyce nazywamy tę właściwość samopodobieństwem, a kształty, które ją posiadają nazywane są fraktalami. Są one jednymi z najpiękniejszych i najbardziej dziwacznych obiektów w całej matematyce.
Aby stworzyć własne fraktale, musimy zacząć od prostego wzoru, a następnie powtarzać go w kółko, w mniejszych skalach.
Jednym z najprostszych wzorów może być odcinek linii, z dwoma kolejnymi odcinkami odgałęziającymi się od jednego końca. Jeśli powtórzymy ten wzór, oba te niebieskie odcinki będą miały jeszcze dwa rozgałęzienia na swoich końcach.
Możesz przesuwać niebieskie kropki, aby zmienić długość i kąt wszystkich rozgałęzień. Następnie zwiększ liczbę iteracji za pomocą suwaka poniżej.
W zależności od położenia gałęzi możesz tworzyć zupełnie inne wzory – wyglądające jak powyższa paproć, drzewo lub zagnieżdżone pięciokąty. Co jeszcze możesz znaleźć?
Innym znanym fraktalem jest trójkąt Sierpińskiego. W tym przypadku zaczynamy od dużego trójkąta równobocznego, a następnie z pozostałych części wielokrotnie wycinamy mniejsze trójkąty.
Zauważ, że ostateczny kształt składa się z trzech identycznych kopii samego siebie, a każda z nich składa się z jeszcze mniejszych kopii całego trójkąta! Mógłbyś powiększać trójkąt w nieskończoność, a wzory i kształty zawsze będą się powtarzać.
Rośliny na początku tego rozdziału wyglądają jak fraktale, ale stworzenie prawdziwych fraktali w prawdziwym życiu jest oczywiście niemożliwe. Gdybyśmy powtarzali w kółko ten sam wzór, coraz mniejszy i mniejszy, doszlibyśmy w końcu do komórek, cząsteczek lub atomów, których nie da się już podzielić.
Jednakże, używając matematyki, możemy zastanowić się nad właściwościami, jakie „miałyby” prawdziwe fraktale – i są one bardzo zaskakujące…
Wymiary fraktali
Na początek zastanówmy się nad wymiarami fraktali. Linia ma wymiar . Przy skalowaniu jej o współczynnik 2, jej długość wzrasta o współczynnik 21=2. Oczywiście!
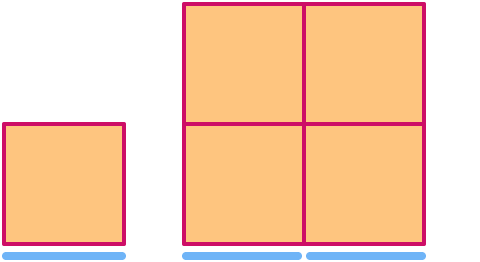
Kwadrat ma wymiar . Przy skalowaniu go o współczynnik 2 jego pole zwiększa się o współczynnik 22= .
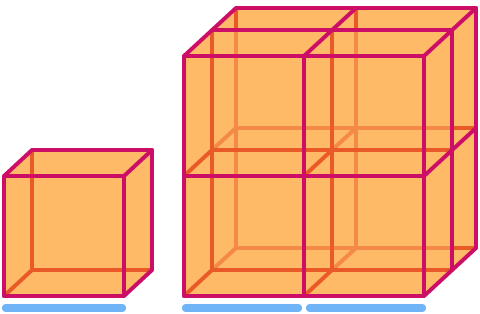
Sześcian ma wymiar . Gdy przeskalujemy go o współczynnik 2, jego objętość zwiększy się o współczynnik 23= . Zauważmy, że większy sześcian na rysunku składa się z 8 kopii mniejszego!
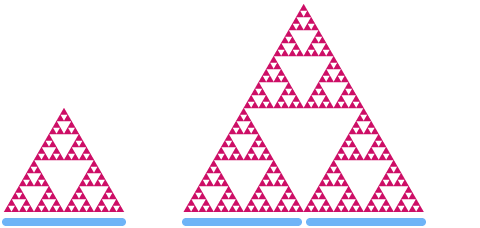
Przyjrzyjmy się teraz trójkątowi Sierpińskiego. Jeśli przeskalujemy go o współczynnik 2, zobaczymy, że jego „obszar” wzrasta o współczynnik .
Powiedzmy, że d jest wymiarem trójkąta Sierpińskiego. Używając tego samego wzoru co powyżej, otrzymujemy 2d=3. Innymi słowy, d = log23log32 ≈ 1.585…
Ale czekaj … jak coś może mieć wymiar, który nie jest liczbą całkowitą? Wydaje się to niemożliwe, ale jest to tylko jedna z dziwnych właściwości fraktali. W rzeczywistości to właśnie nadaje fraktalom ich nazwę: mają one wymiar ułamkowy.
Z każdą iteracją usuwamy część obszaru trójkąta Sierpińskiego. Gdybyśmy mogli robić to nieskończenie wiele razy, to w rzeczywistości nie pozostałby żaden obszar: dlatego trójkąt Sierpińskiego jest czymś pomiędzy dwuwymiarowym obszarem, a jednowymiarową linią.
Pomimo, że wiele fraktali jest samopodobnych, lepszą definicją jest to, że fraktale są kształtami, które mają wymiar inny niż całkowity.
Płatek śniegu Kocha
W przyrodzie jest wiele kształtów, które wyglądają jak fraktale. Widzieliśmy już kilka roślin na początku tego rozdziału. Inne wspaniałe przykłady to płatki śniegu i kryształy lodu:
Aby stworzyć nasz własny fraktalny płatek śniegu, ponownie musimy znaleźć prostą procedurę, którą będziemy mogli stosować w kółko.
Podobnie jak w przypadku trójkąta Sierpińskiego, zacznijmy od pojedynczego trójkąta równobocznego. Jednak zamiast usuwać mniejsze trójkąty na każdym kroku, dodajemy mniejsze trójkąty wzdłuż krawędzi. Długość boku każdego trójkąta to 131412 trójkątów z poprzedniego kroku.
Otrzymany kształt nazywamy płatkiem śniegu Kocha, nazwanym tak na cześć szwedzkiego matematyka Helge von Kocha. Zauważ jeszcze raz, że małe odcinki krawędzi płatka śniegu wyglądają dokładnie tak samo jak większe odcinki.
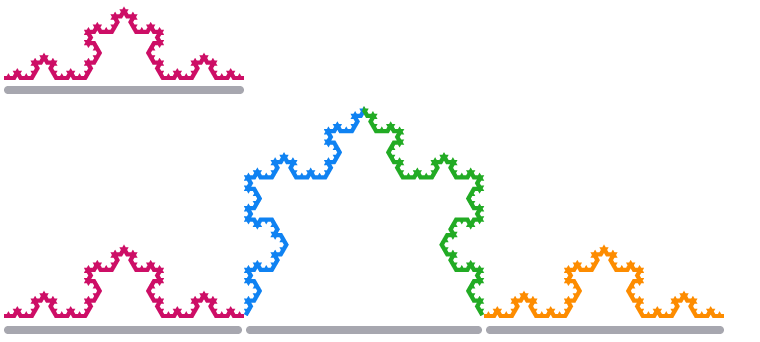
Gdy przeskalujemy jeden odcinek krawędzi płatka śniegu Kocha o współczynnik 3, jego długość zwiększy się czterokrotnie.
Używając tej samej relacji między wymiarami i współczynnikami skali co powyżej, otrzymujemy równanie 3d=42d=42d=34d=3. Oznacza to, że wymiar płatka śniegu Kocha wynosi d=log34≈1,262.
Area
Tworzenie płatków śniegu Kocha jest prawie jak sekwencja rekurencyjna: znamy kształt początkowy (trójkąt) i wiemy, jak przejść od jednego terminu do następnego (dodając więcej trójkątów na każdej krawędzi):


nowe trójkąty

nowe trójkąty

nowe trójkąty
Po pierwszej iteracji liczba dodawanych nowych trójkątów wzrasta o współczynnik na każdym kroku. Jednocześnie powierzchnia tych nowych trójkątów maleje o współczynnik przy każdym kroku.
Powiedzmy, że pierwszy trójkąt ma powierzchnię 1. Wtedy całkowita powierzchnia kolejnych trzech trójkątów wynosi 3×19=13. Wszystkie kolejne kroki tworzą szereg geometryczny szereg arytmetyczny szereg kwadratowy o wspólnym współczynniku 499443.
Korzystając ze wzoru na sumę nieskończonych szeregów geometrycznych, możemy obliczyć, że całkowite pole płatka śniegu Kocha wynosi
A=1+13×11-491+949-14=85=1.6.
Perymetr
Możemy również spróbować obliczyć obwód płatka śniegu Kocha. Jak już widzieliśmy wcześniej, długość obwodu zmienia się o współczynnik 433414 na każdym kroku.
Oznacza to, że po raz kolejny mamy szereg geometryczny – ale w tym przypadku nie jest on zbieżnyeconverges do 0doesn’t have a first term. Oznacza to, że obwód płatka śniegu Kocha jest w rzeczywistości nieskończenie długi!

Jeśli wydaje się to sprzeczne z intuicją, po prostu pamiętaj, że mnożymy obwód przez 43 na każdym kroku i robimy to nieskończenie wiele razy.
To prawie nie do pomyślenia, że można mieć kształt o skończonej powierzchni i jednocześnie nieskończonym obwodzie – ale to tylko jedna z wielu nieoczekiwanych właściwości fraktali.
Czy możesz wymyślić jakieś inne sposoby tworzenia własnych fraktali?
„My soul is spiralling on frozen fractals all around…”
Menger Sponge
Fraktale nie muszą być „płaskie”, jak wiele z powyższych przykładów. Jednym z najbardziej znanych fraktali, które wyglądają na trójwymiarowe, jest gąbka Mengera, nazwana tak na cześć matematyka Karla Mengera, który po raz pierwszy opisał ją w 1926 roku.
Zaczynamy od litego sześcianu i wielokrotnie wiercimy coraz mniejsze otwory w jego ścianach. Każda nowa iteracja otworów ma 131214 szerokości poprzedniej iteracji otworów.
Sześcian 3×3×3 składa się z 27 mniejszych sześcianów, ale tutaj usunęliśmy niektóre z nich. Gąbka Mengera składa się z kopii samej siebie, które są 3 razy mniejsze.
Teraz możemy spróbować obliczyć wymiar d gąbki Mengera tak jak zrobiliśmy to dla płatka śniegu Kocha powyżej. W tym przypadku otrzymamy 3d=20, czyli d=log320≈2,727.
Jeśli wyobrazimy sobie wycinanie coraz większej ilości otworów, nieskończenie wiele razy, to nie pozostanie nam żadna rzeczywista objętość. Dlatego właśnie sześcian jest „nie całkiem” trójwymiarowy!
Fraktalne linie brzegowe
Jedną z kluczowych cech wszystkich fraktali, które widzieliśmy do tej pory, jest to, że możesz „powiększać” w nieskończoność i zawsze znajdziesz nowe wzory. Około 1920 roku, brytyjski matematyk Lewis Fry Richardson zdał sobie sprawę, że to samo jest prawdą dla granicy lub linii brzegowej wielu krajów.
Zaczynasz od podstawowego kształtu kraju, a w miarę powiększania dodajesz ujścia rzek, zatoki i estuaria, następnie pojedyncze klify, skały, otoczaki i tak dalej:
Jest to istotny problem, gdy próbujemy obliczyć długość granicy jakiegoś kraju – jak zdecydować, jak daleko powiększyć i które zakamarki uwzględnić?
Jednym ze sposobów, w jaki moglibyśmy zmierzyć długość linii brzegowej Wielkiej Brytanii, na przykład, jest wzięcie długiej linijki, obejście jej plaż dookoła, a następnie zsumowanie wszystkich odległości.
Jeśli linijka ma długość ${rulers}km, musimy jej użyć ${count} razy, więc otrzymujemy całkowitą linię brzegową o długości ${count} × ${count} × ${rulers} = ${count * rulers}km.
Możemy po prostu kontynuować, z coraz mniejszymi linijkami, a za każdym razem nasz wynik długości linii brzegowej trochę się wydłuży. Tak jak wcześniej w przypadku płatka śniegu Kocha, wydaje się, że linia brzegowa Wielkiej Brytanii jest nieskończenie długa! To jest często nazywane paradoksem linii brzegowej.
Kilka dekad później, matematyk Benoit Mandelbrot natknął się na pracę Richardsona w porzuconej książce bibliotecznej, podczas pracy w IBM. Dostrzegł jej znaczenie, a także to, jak odnosi się ona do nowszych badań nad fraktalami i wymiarami.
Linia brzegowa Wielkiej Brytanii z pewnością „wygląda” na fraktalną, ale nie jest samopodobna, jak inne fraktale, które widzieliśmy wcześniej. Aby znaleźć jego rozmiar, możemy narysować go na siatce i policzyć liczbę komórek, z którymi się przecina.
Początkowo jest 88 przecinających się komórek. Jeśli przeskalujemy linię brzegową o współczynnik 2, otrzymamy 197 przecinających się komórek – ponad dwa razy więcej!
Rozmiar linii brzegowej zwiększył się o współczynnik 19788. Podobnie jak poprzednio, oznacza to, że wymiar linii brzegowej wynosi
d=log219788≈1.16
Gdybyśmy powtórzyli to z większymi siatkami, okazałoby się, że wymiar linii brzegowej Wielkiej Brytanii wynosi w rzeczywistości około 1.21. Mandelbrot zdał sobie sprawę, że ten wymiar fraktalny jest również miarą chropowatości kształtu – to nowa koncepcja, dla której znalazł ważne zastosowania w wielu innych dziedzinach matematyki i nauki.
Więcej fraktali w przyrodzie i technologii
Choć prawdziwe fraktale nigdy nie mogą pojawić się w przyrodzie, istnieje wiele obiektów, które wyglądają prawie jak fraktale. Widzieliśmy już rośliny, płatki śniegu i linie brzegowe, a oto kilka kolejnych przykładów:
Pasmo górskie w środkowej Azji
Delta rzeki Ganges w Indiach
Błyskawice
. Naczynia krwionośne w siatkówce
Wielki Kanion w USA
Chmury
Wszystkie te obiekty mogą wydawać się zupełnie przypadkowe, ale, tak jak w przypadku fraktali, istnieje podstawowy wzór, który określa sposób ich powstawania. Matematyka może pomóc nam lepiej zrozumieć te kształty, a fraktale mają zastosowanie w takich dziedzinach jak medycyna, biologia, geologia i meteorologia.
Generowany komputerowo teren fraktalny
Możemy również używać fraktali do tworzenia realistycznych „kopii” natury, na przykład jako krajobrazów i tekstur używanych w grach wideo lub filmach generowanych komputerowo. Woda, góry i chmury na tym obrazie zostały wykonane w całości przez komputer, z pomocą fraktali!
I możemy nawet odwrócić ten proces do kompresji obrazów cyfrowych, aby zmniejszyć ich rozmiar. Pierwsze algorytmy zostały opracowane przez Michaela Barnsleya i Alana Sloana w latach 80-tych, a nowe są badane do dziś.