Regresión Logística

La regresión logística (también conocida como regresión logit o modelo logit) fue desarrollada por el estadístico David Cox en 1958 y es un modelo de regresión donde la variable de respuesta Y es categórica. La regresión logística nos permite estimar la probabilidad de una respuesta categórica en función de una o más variables predictoras (X). Permite decir que la presencia de un predictor aumenta (o disminuye) la probabilidad de un resultado determinado en un porcentaje específico. Este tutorial cubre el caso en el que Y es binario, es decir, cuando sólo puede tomar dos valores, «0» y «1», que representan resultados como aprobado/no aprobado, ganar/perder, vivo/muerto o sano/enfermo. Los casos en los que la variable dependiente tiene más de dos categorías de resultados pueden analizarse con la regresión logística multinomial o, si las categorías múltiples están ordenadas, en la regresión logística ordinal. Sin embargo, el análisis discriminante se ha convertido en un método popular para la clasificación multiclase, por lo que nuestro próximo tutorial se centrará en esa técnica para esos casos.

tl;dr

Este tutorial sirve como introducción a la regresión logística y cubre1:

1. Requisitos de replicación: Lo que necesitará para reproducir el análisis de este tutorial
2. Por qué la regresión logística: ¿Por qué utilizar la regresión logística?
3. Preparar nuestros datos: Preparar nuestros datos para el modelado
4. Regresión logística simple: Predecir la probabilidad de la respuesta Y con una sola variable predictora X
5. Regresión logística múltiple: Predicción de la probabilidad de respuesta Y con múltiples variables predictoras
6. Diagnóstico de la evaluación del modelo &: ¿Qué tan bien se ajusta el modelo a los datos? Qué predictores son los más importantes? ¿Son precisas las predicciones?

Requisitos de replicación

Este tutorial aprovecha principalmente los datos Defaultproporcionados por el paquete ISLR. Se trata de un conjunto de datos simulados que contiene información sobre diez mil clientes, como por ejemplo, si el cliente es moroso, si es estudiante, el saldo medio que lleva el cliente y los ingresos del cliente. También utilizaremos algunos paquetes que proporcionan funciones de manipulación de datos, visualización, modelado de tuberías y ordenación de los resultados del modelo.

# Packageslibrary(tidyverse) # data manipulation and visualizationlibrary(modelr) # provides easy pipeline modeling functionslibrary(broom) # helps to tidy up model outputs# Load data (default <- as_tibble(ISLR::Default))## # A tibble: 10,000 × 4## default student balance income## <fctr> <fctr> <dbl> <dbl>## 1 No No 729.5265 44361.625## 2 No Yes 817.1804 12106.135## 3 No No 1073.5492 31767.139## 4 No No 529.2506 35704.494## 5 No No 785.6559 38463.496## 6 No Yes 919.5885 7491.559## 7 No No 825.5133 24905.227## 8 No Yes 808.6675 17600.451## 9 No No 1161.0579 37468.529## 10 No No 0.0000 29275.268## # ... with 9,990 more rows

Por qué la regresión logística

La regresión lineal no es apropiada en el caso de una respuesta cualitativa. ¿Por qué no? Supongamos que intentamos predecir el estado de salud de una paciente en la sala de urgencias a partir de sus síntomas. En este ejemplo simplificado, hay tres posibles diagnósticos: apoplejía, sobredosis de drogas y ataque epiléptico. Podríamos considerar la codificación de estos valores como una variable de respuesta cuantitativa, Y , de la siguiente manera:

Usando esta codificación, se podrían utilizar los mínimos cuadrados para ajustar un modelo de regresión lineal para predecir Y sobre la base de un conjunto de predictores . Desgraciadamente, esta codificación implica una ordenación de los resultados, situando la sobredosis de medicamentos entre el ictus y el ataque epiléptico, e insistiendo en que la diferencia entre el ictus y la sobredosis de medicamentos es la misma que la diferencia entre la sobredosis de medicamentos y el ataque epiléptico. En la práctica, no hay ninguna razón especial para que esto sea así. Por ejemplo, se podría elegir una codificación igualmente razonable,

que implicaría una relación totalmente diferente entre las tres condiciones. Cada una de estas codificaciones produciría modelos lineales fundamentalmente diferentes que, en última instancia, darían lugar a diferentes conjuntos de predicciones sobre las observaciones de prueba.

Más relevante para nuestros datos, si intentamos clasificar a un cliente como moroso de alto o bajo riesgo en función de su saldo, podríamos utilizar la regresión lineal; sin embargo, la figura de la izquierda ilustra cómo la regresión lineal predeciría la probabilidad de impago. Desgraciadamente, para saldos cercanos a cero predecimos una probabilidad negativa de impago; si hiciéramos la predicción para saldos muy grandes, obtendríamos valores mayores que 1. Estas predicciones no son sensatas, ya que, por supuesto, la verdadera probabilidad de impago, independientemente del saldo de la tarjeta de crédito, debe estar entre 0 y 1.

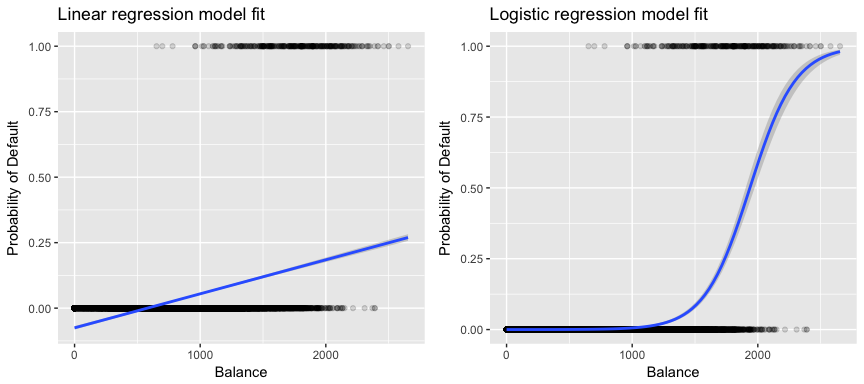
Para evitar este problema, debemos modelar p(X) utilizando una función que dé resultados entre 0 y 1 para todos los valores de X. Muchas funciones cumplen esta descripción. En la regresión logística, utilizamos la función logística, que se define en la Ecuación 1 y se ilustra en la figura de la derecha.

Preparación de nuestros datos

Como en el tutorial de regresión, dividiremos nuestros datos en un conjunto de datos de entrenamiento (60%) y otro de prueba (40%) para poder evaluar el rendimiento de nuestro modelo en un conjunto de datos fuera de la muestra.

set.seed(123)sample <- sample(c(TRUE, FALSE), nrow(default), replace = T, prob = c(0.6,0.4))train <- defaulttest <- default

Regresión Logística Simple

Ajustaremos un modelo de regresión logística con el fin de predecir la probabilidad de que un cliente entre en mora en base al saldo medio que lleva el cliente. La función glm ajusta modelos lineales generalizados, una clase de modelos que incluye la regresión logística. La sintaxis de la función glm es similar a la de lm, excepto que debemos pasar el argumento family = binomial para decirle a R que ejecute una regresión logística en lugar de otro tipo de modelo lineal generalizado.

model1 <- glm(default ~ balance, family = "binomial", data = train)

En el fondo, la función glm, utiliza la máxima probabilidad para ajustar el modelo. La intuición básica que subyace al uso de la máxima verosimilitud para ajustar un modelo de regresión logística es la siguiente: buscamos estimaciones para y tales que la probabilidad de impago predicha para cada individuo, utilizando la Ecuación 1, se corresponda lo más posible con el estado de impago observado del individuo. En otras palabras, tratamos de encontrar y de tal manera que al introducir estas estimaciones en el modelo para p(X), dado en la Ecuación 1, se obtenga un número cercano a uno para todos los individuos que incumplieron, y un número cercano a cero para todos los individuos que no lo hicieron. Esta intuición puede formalizarse mediante una ecuación matemática denominada función de verosimilitud:

Las estimaciones y se eligen para maximizar esta función de verosimilitud. La máxima verosimilitud es un enfoque muy general que se utiliza para ajustar muchos de los modelos no lineales que examinaremos en futuros tutoriales. Lo que resulta es una curva de probabilidad en forma de S que se ilustra a continuación (tenga en cuenta que para trazar la línea de ajuste de la regresión logística tenemos que convertir nuestra variable de respuesta en una variable codificada binaria).

default %>% mutate(prob = ifelse(default == "Yes", 1, 0)) %>% ggplot(aes(balance, prob)) + geom_point(alpha = .15) + geom_smooth(method = "glm", method.args = list(family = "binomial")) + ggtitle("Logistic regression model fit") + xlab("Balance") + ylab("Probability of Default")

De forma similar a la regresión lineal, podemos evaluar el modelo utilizando summary o glance. Tenga en cuenta que el formato de salida del coeficiente es similar a lo que vimos en la regresión lineal; sin embargo, los detalles de bondad de ajuste en la parte inferior de summary difieren. Nos ocuparemos de esto más adelante, pero sólo observe que ve la palabra desviación. La desviación es análoga a los cálculos de la suma de cuadrados en la regresión lineal y es una medida de la falta de ajuste a los datos en un modelo de regresión logística. La desviación nula representa la diferencia entre un modelo con sólo el intercepto (que significa «sin predictores») y un modelo saturado (un modelo con un ajuste teóricamente perfecto). El objetivo es que la desviación del modelo (anotada como desviación residual) sea menor; los valores más pequeños indican un mejor ajuste. En este sentido, el modelo nulo proporciona una línea de base sobre la que comparar los modelos de predicción.

summary(model1)## ## Call:## glm(formula = default ~ balance, family = "binomial", data = train)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.2905 -0.1395 -0.0528 -0.0189 3.3346 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.101e+01 4.887e-01 -22.52 <2e-16 ***## balance 5.669e-03 2.949e-04 19.22 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 1723.03 on 6046 degrees of freedom## Residual deviance: 908.69 on 6045 degrees of freedom## AIC: 912.69## ## Number of Fisher Scoring iterations: 8

Evaluación de los coeficientes

La siguiente tabla muestra las estimaciones de los coeficientes y la información relacionada que resulta del ajuste de un modelo de regresión logística para predecir la probabilidad de impago = Sí utilizando el equilibrio. Tenga en cuenta que las estimaciones de los coeficientes de la regresión logística caracterizan la relación entre el predictor y la variable de respuesta en una escala de logaritmos (véase el capítulo 3 de ISLR1 para más detalles). Así, vemos que ; esto indica que un aumento del saldo está asociado a un aumento de la probabilidad de impago. Para ser precisos, un aumento de una unidad en el saldo se asocia con un aumento de las probabilidades logarítmicas de impago en 0,0057 unidades.

tidy(model1)## term estimate std.error statistic p.value## 1 (Intercept) -11.006277528 0.488739437 -22.51972 2.660162e-112## 2 balance 0.005668817 0.000294946 19.21985 2.525157e-82

Podemos interpretar además el coeficiente de saldo como: por cada aumento de un dólar en el saldo mensual, las probabilidades de impago del cliente se multiplican por un factor.0057.

exp(coef(model1))## (Intercept) balance ## 1.659718e-05 1.005685e+00

Muchos aspectos de la salida del coeficiente son similares a los discutidos en la salida de la regresión lineal. Por ejemplo, podemos medir los intervalos de confianza y la precisión de las estimaciones de los coeficientes calculando sus errores estándar. Por ejemplo, tiene un valor p < 2e-16 que sugiere una relación estadísticamente significativa entre el balance llevado y la probabilidad de impago. También podemos utilizar los errores estándar para obtener intervalos de confianza como hicimos en el tutorial de regresión lineal:

confint(model1)## 2.5 % 97.5 %## (Intercept) -12.007610373 -10.089360652## balance 0.005111835 0.006269411

Hacer predicciones

Una vez estimados los coeficientes, es sencillo calcular la probabilidad de impago para cualquier saldo de tarjeta de crédito. Matemáticamente, utilizando las estimaciones de los coeficientes de nuestro modelo, predecimos que la probabilidad de impago para un individuo con un saldo de 1.000 dólares es inferior al 0,5%

Podemos predecir la probabilidad de impago en R utilizando la función predict (asegúrese de incluir type = "response"). Aquí comparamos la probabilidad de impago basándonos en saldos de 1000$ y 2000$. Como puede ver, a medida que el saldo pasa de 1.000 a 2.000 dólares, la probabilidad de impago aumenta significativamente, ¡del 0,5% al 58%!

predict(model1, data.frame(balance = c(1000, 2000)), type = "response")## 1 2 ## 0.004785057 0.582089269

También se pueden utilizar predictores cualitativos con el modelo de regresión logística. Como ejemplo, podemos ajustar un modelo que utilice la variable student.

model2 <- glm(default ~ student, family = "binomial", data = train)tidy(model2)## term estimate std.error statistic p.value## 1 (Intercept) -3.5534091 0.09336545 -38.05914 0.000000000## 2 studentYes 0.4413379 0.14927208 2.95660 0.003110511

El coeficiente asociado a student = Yes es positivo, y el valor p asociado es estadísticamente significativo. Esto indica que los estudiantes tienden a tener mayores probabilidades de impago que los no estudiantes. De hecho, este modelo sugiere que un estudiante tiene casi el doble de probabilidades de impago que los no estudiantes. Sin embargo, en la siguiente sección veremos por qué.

predict(model2, data.frame(student = factor(c("Yes", "No"))), type = "response")## 1 2 ## 0.04261206 0.02783019

Regresión Logística Múltiple

También podemos ampliar nuestro modelo como se ve en la Ec. 1 de modo que podamos predecir una respuesta binaria utilizando predictores múltiples donde son p predictores:

Vamos a ajustar un modelo que predice la probabilidad de impago basado en las variables de saldo, ingresos (en miles de dólares) y situación de estudiante. Hay un resultado sorprendente aquí. Los valores p asociados al saldo y a la condición de estudiante son muy pequeños, lo que indica que cada una de estas variables está asociada a la probabilidad de impago. Sin embargo, el coeficiente de la variable estudiante es negativo, lo que indica que los estudiantes tienen menos probabilidades de impago que los no estudiantes. Por el contrario, el coeficiente de la variable estudiante en el modelo 2, en el que predecimos la probabilidad de impago basándonos sólo en la condición de estudiante, indica que los estudiantes tienen una mayor probabilidad de impago. ¿Qué ocurre?

model3 <- glm(default ~ balance + income + student, family = "binomial", data = train)tidy(model3)## term estimate std.error statistic p.value## 1 (Intercept) -1.090704e+01 6.480739e-01 -16.8299277 1.472817e-63## 2 balance 5.907134e-03 3.102425e-04 19.0403764 7.895817e-81## 3 income -5.012701e-06 1.078617e-05 -0.4647343 6.421217e-01## 4 studentYes -8.094789e-01 3.133150e-01 -2.5835947 9.777661e-03

El panel derecho de la figura siguiente ofrece una explicación para esta discrepancia. Las variables estudiante y saldo están correlacionadas. Los estudiantes tienden a tener mayores niveles de deuda, lo que a su vez se asocia con una mayor probabilidad de impago. En otras palabras, los estudiantes son más propensos a tener grandes saldos en sus tarjetas de crédito, que, como sabemos por el panel izquierdo de la siguiente figura, tienden a estar asociados con altas tasas de impago. Por lo tanto, aunque un estudiante individual con un determinado saldo de tarjeta de crédito tenderá a tener una menor probabilidad de impago que un no estudiante con el mismo saldo de tarjeta de crédito, el hecho de que los estudiantes en su conjunto tiendan a tener mayores saldos de tarjeta de crédito significa que, en general, los estudiantes tienden a incumplir con una tasa más alta que los no estudiantes. Esta es una distinción importante para una empresa de tarjetas de crédito que intenta determinar a quién debe ofrecer crédito. Un estudiante es más arriesgado que un no estudiante si no se dispone de información sobre el saldo de la tarjeta de crédito del estudiante. Sin embargo, ¡ese estudiante es menos arriesgado que un no estudiante con el mismo saldo de tarjeta de crédito!

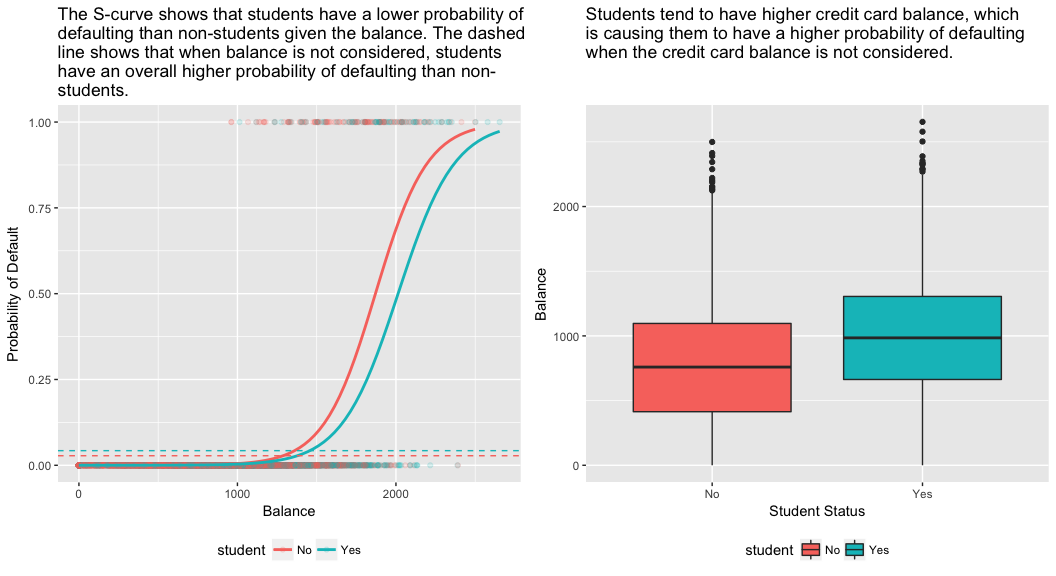
Este sencillo ejemplo ilustra los peligros y las sutilezas asociadas a la realización de regresiones con un único predictor cuando otros predictores pueden ser también relevantes. Los resultados obtenidos utilizando un solo predictor pueden ser muy diferentes de los obtenidos utilizando múltiples predictores, especialmente cuando hay correlación entre los predictores. Este fenómeno se conoce como confusión.

En el caso de múltiples variables predictoras a veces queremos entender qué variable es la más influyente en la predicción de la variable de respuesta (Y). Podemos hacerlo con varImp del paquete caret. En este caso, vemos que el saldo es el más importante por un amplio margen, mientras que la condición de estudiante es menos importante, seguida de los ingresos (que, de todos modos, resultaron insignificantes (p = 0,64)).

caret::varImp(model3)## Overall## balance 19.0403764## income 0.4647343## studentYes 2.5835947

Como antes, podemos hacer predicciones fácilmente con este modelo. Por ejemplo, un estudiante con un saldo de tarjeta de crédito de 1.500 dólares y unos ingresos de 40.000 dólares tiene una probabilidad estimada de impago de

Un no estudiante con el mismo saldo e ingresos tiene una probabilidad estimada de impago de

new.df <- tibble(balance = 1500, income = 40, student = c("Yes", "No"))predict(model3, new.df, type = "response")## 1 2 ## 0.05437124 0.11440288

Así, vemos que para el saldo y los ingresos dados (aunque los ingresos son insignificantes) un estudiante tiene aproximadamente la mitad de probabilidad de impago que un no estudiante.

Evaluación del modelo &Diagnóstico

Hasta ahora se han construido tres modelos de regresión logística y se han examinado los coeficientes. Sin embargo, quedan algunas preguntas críticas. ¿Son buenos los modelos? ¿Cómo se ajusta el modelo a los datos? En el tutorial de regresión lineal vimos cómo el estadístico F y los diagnósticos ajustados y residuales nos informan de lo bien que el modelo se ajusta a los datos. Aquí veremos algunas formas de evaluar la bondad de ajuste de nuestros modelos logit.

Prueba de relación de verosimilitud

En primer lugar, podemos utilizar una prueba de relación de verosimilitud para evaluar si nuestros modelos están mejorando el ajuste. Añadir variables predictoras a un modelo casi siempre mejorará el ajuste del modelo (es decir, aumentará la probabilidad logarítmica y reducirá la desviación del modelo en comparación con la desviación nula), pero es necesario probar si la diferencia observada en el ajuste del modelo es estadísticamente significativa. Podemos utilizar anova para realizar esta prueba. Los resultados indican que, en comparación con model1, model3 reduce la desviación residual en más de 13 (recuerde, un objetivo de la regresión logística es encontrar un modelo que minimice los residuos de desviación). Y lo que es más importante, esta mejora es estadísticamente significativa a p = 0,001. Esto sugiere que model3 proporciona un mejor ajuste del modelo.

anova(model1, model3, test = "Chisq")## Analysis of Deviance Table## ## Model 1: default ~ balance## Model 2: default ~ balance + income + student## Resid. Df Resid. Dev Df Deviance Pr(>Chi) ## 1 6045 908.69 ## 2 6043 895.02 2 13.668 0.001076 **## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pseudo

A diferencia de la regresión lineal con estimación de mínimos cuadrados ordinarios, no existe un estadístico que explique la proporción de la varianza en la variable dependiente que es explicada por los predictores. Sin embargo, hay una serie de pseudomedidores que podrían ser útiles. El más notable es el de McFadden, que se define como

donde es el valor de la probabilidad logarítmica para el modelo ajustado y es la probabilidad logarítmica para el modelo nulo con sólo un intercepto como predictor. La medida oscila entre 0 y algo menos de 1, y los valores más cercanos a cero indican que el modelo no tiene poder predictivo. Sin embargo, a diferencia de lo que ocurre en la regresión lineal, los modelos rara vez alcanzan un valor de McFadden alto. De hecho, en palabras del propio McFadden, los modelos con un pseudo McFadden representan un ajuste muy bueno. Podemos evaluar los valores del pseudo de McFadden para nuestros modelos con:

list(model1 = pscl::pR2(model1), model2 = pscl::pR2(model2), model3 = pscl::pR2(model3))## $model1## McFadden ## 0.4726215 ## ## $model2## McFadden ## 0.004898314 ## ## $model3## McFadden ## 0.4805543

Vemos que el modelo 2 tiene un valor muy bajo que corrobora su mal ajuste. Sin embargo, los modelos 1 y 3 son mucho más altos, lo que sugiere que explican una buena cantidad de varianza en los datos por defecto. Además, vemos que el modelo 3 sólo mejora ligeramente.

Evaluación de los residuos

Tenga en cuenta que la regresión logística no supone que los residuos se distribuyan normalmente ni que la varianza sea constante. Sin embargo, el residuo de desviación es útil para determinar si los puntos individuales no se ajustan bien al modelo. Aquí podemos ajustar los residuos de desviación estandarizados para ver cuántos superan las 3 desviaciones estándar. Primero extraemos varias partes útiles de los resultados del modelo con augment y luego procedemos a graficar.

model1_data <- augment(model1) %>% mutate(index = 1:n())ggplot(model1_data, aes(index, .std.resid, color = default)) + geom_point(alpha = .5) + geom_ref_line(h = 3)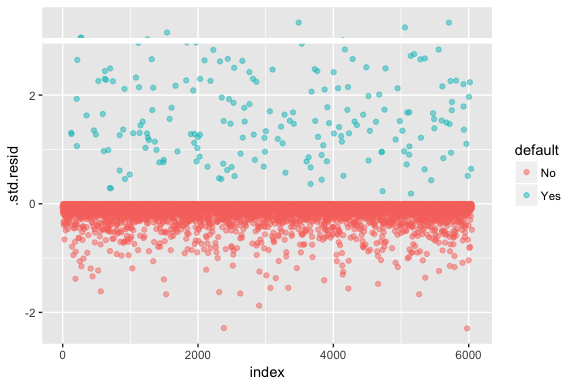

Los residuos estandarizados que exceden de 3 representan posibles valores atípicos y pueden merecer mayor atención. Podemos filtrar estos residuos para obtener una mirada más cercana. Vemos que todas estas observaciones representan a clientes que incumplieron con presupuestos mucho más bajos que los morosos normales.

model1_data %>% filter(abs(.std.resid) > 3)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 Yes 1118.7010 -4.664566 0.1752745 3.057432 0.0002841609 0.3857438 0.01508609 3.057867 271## 2 Yes 1119.0972 -4.662320 0.1751742 3.056704 0.0002844621 0.3857448 0.01506820 3.057139 272## 3 Yes 1135.0473 -4.571902 0.1711544 3.027272 0.0002967274 0.3857832 0.01435943 3.027721 1253## 4 Yes 1066.8841 -4.958307 0.1885550 3.151288 0.0002463229 0.3856189 0.01754100 3.151676 1542## 5 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 6 Yes 1143.6805 -4.522962 0.1689933 3.011233 0.0003034789 0.3858039 0.01398491 3.011690 4142## 7 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 8 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709

De forma similar a la regresión lineal, también podemos identificar las observaciones influyentes con los valores de distancia de Cook. Aquí identificamos los 5 valores más grandes.

plot(model1, which = 4, id.n = 5)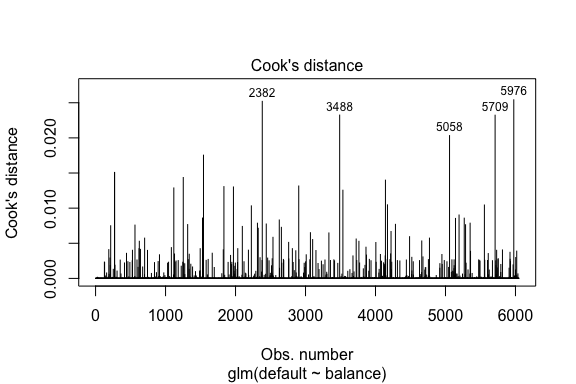

Y también podemos investigarlos más a fondo. Aquí vemos que los cinco puntos más influyentes incluyen:

• aquellos clientes que incumplieron con saldos muy bajos y
• dos clientes que no incumplieron, pero que tenían saldos de más de 2.000 dólares

Esto significa que si elimináramos estas observaciones (no se recomienda), la forma, la ubicación y el intervalo de confianza de nuestra curva S de regresión logística probablemente cambiarían.

model1_data %>% top_n(5, .cooksd)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 No 2388.1740 2.531843 0.2413764 -2.284011 0.0039757771 0.3866249 0.02520100 -2.288565 2382## 2 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 3 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 4 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709## 5 No 2391.0077 2.547907 0.2421522 -2.290521 0.0039468742 0.3866185 0.02542145 -2.295054 5976

Validación de los valores predichos

Tasa de clasificación

Cuando se desarrollan modelos de predicción, la métrica más crítica es la relativa a lo bien que el modelo predice la variable objetivo en las observaciones fuera de la muestra. En primer lugar, tenemos que utilizar los modelos estimados para predecir valores en nuestro conjunto de datos de entrenamiento (train). Cuando utilice predict asegúrese de incluir type = response para que la predicción devuelva la probabilidad de incumplimiento.

test.predicted.m1 <- predict(model1, newdata = test, type = "response")test.predicted.m2 <- predict(model2, newdata = test, type = "response")test.predicted.m3 <- predict(model3, newdata = test, type = "response")

Ahora podemos comparar la variable objetivo predicha frente a los valores observados para cada modelo y ver cuál rinde mejor. Podemos empezar utilizando la matriz de confusión, que es una tabla que describe el rendimiento de la clasificación para cada modelo en los datos de prueba. Cada cuadrante de la tabla tiene un significado importante. En este caso, los «No» y «Sí» de las filas representan si los clientes incumplieron o no. Los «FALSO» y «VERDADERO» de las columnas representan si predijimos que los clientes incumplirían o no.

• Verdaderos positivos (cuadrante inferior derecho): son casos en los que predijimos que el cliente incumpliría y lo hizo.
• Verdaderos negativos (cuadrante superior izquierdo): Predijimos que no habría impago y el cliente no lo hizo.
• falsos positivos (cuadrante superior derecho): Predijimos que sí, pero no se produjo el impago. (También conocido como «error de tipo I».)
• falsos negativos (parte inferior izquierda): Predijimos que no, pero sí incumplieron. (También conocido como «error de tipo II»)

Los resultados muestran que model1 y model3 son muy similares. El 96% de las observaciones predichas son verdaderos negativos y alrededor del 1% son verdaderos positivos. Ambos modelos tienen un error de tipo II de menos del 3% en el que el modelo predice que el cliente no va a incumplir pero en realidad lo hizo. Y ambos modelos tienen un error de tipo I de menos del 1% en el que los modelos predicen que el cliente incumplirá pero nunca lo hizo. Los resultados de model2 son notablemente diferentes; este modelo predice con exactitud a los no morosos (un resultado del 97% de los datos que son no morosos) pero nunca predice realmente a los clientes que incumplen!

list( model1 = table(test$default, test.predicted.m1 > 0.5) %>% prop.table() %>% round(3), model2 = table(test$default, test.predicted.m2 > 0.5) %>% prop.table() %>% round(3), model3 = table(test$default, test.predicted.m3 > 0.5) %>% prop.table() %>% round(3))## $model1## ## FALSE TRUE## No 0.962 0.003## Yes 0.025 0.010## ## $model2## ## FALSE## No 0.965## Yes 0.035## ## $model3## ## FALSE TRUE## No 0.963 0.003## Yes 0.026 0.009

También queremos entender las tasas de error de clasificación (también conocido como error) (o podríamos invertir esto para las tasas de precisión). No vemos una gran mejora entre los modelos 1 y 3 y, aunque el modelo 2 tiene una tasa de error baja, no hay que olvidar que nunca predice con exactitud a los clientes que realmente no cumplen con sus obligaciones.

test %>% mutate(m1.pred = ifelse(test.predicted.m1 > 0.5, "Yes", "No"), m2.pred = ifelse(test.predicted.m2 > 0.5, "Yes", "No"), m3.pred = ifelse(test.predicted.m3 > 0.5, "Yes", "No")) %>% summarise(m1.error = mean(default != m1.pred), m2.error = mean(default != m2.pred), m3.error = mean(default != m3.pred))## # A tibble: 1 × 3## m1.error m2.error m3.error## <dbl> <dbl> <dbl>## 1 0.02782697 0.03491019 0.02807994

Podemos obtener información adicional observando los valores brutos (no los porcentajes) en nuestra matriz de confusión. Veamos el modelo 1 para ilustrarlo. Vemos que hay un total de clientes que incumplieron. Del total de impagos, no se predijeron. Alternativamente, podríamos decir que sólo se predijeron los impagos, lo que se conoce como la precisión (también conocida como sensibilidad) de nuestro modelo. Así que mientras la tasa de error global es baja, la tasa de precisión también es baja, lo que no es bueno. Como se ha mencionado anteriormente, la sensibilidad es sinónimo de precisión. Sin embargo, la especificidad es el porcentaje de no infractores que se identifican correctamente, aquí (la precisión aquí es en gran medida impulsada por el hecho de que el 97% de las observaciones en nuestros datos son no infractores). La importancia entre la sensibilidad y la especificidad depende del contexto. En este caso, es probable que una empresa de tarjetas de crédito esté más preocupada por la sensibilidad, ya que quiere reducir su riesgo. Por lo tanto, pueden estar más preocupados por afinar un modelo para que su sensibilidad/precisión mejore.

La característica operativa de recepción (ROC) es una medida visual del rendimiento del clasificador. Utilizando la proporción de puntos de datos positivos que se consideran correctamente como positivos y la proporción de puntos de datos negativos que se consideran erróneamente como positivos, generamos un gráfico que muestra el compromiso entre la tasa a la que se puede predecir correctamente algo con la tasa de predecir incorrectamente algo. En última instancia, nos interesa el área bajo la curva ROC, o AUC. Esta métrica oscila entre 0,50 y 1,00, y los valores superiores a 0,80 indican que el modelo hace un buen trabajo al discriminar entre las dos categorías que componen nuestra variable objetivo. Podemos comparar el ROC y el AUC de los modelos 1 y 2, que muestran una gran diferencia de rendimiento. Definitivamente queremos que nuestros gráficos ROC se parezcan más a los del modelo 1 (izquierda) que a los del modelo 2 (derecha)!

library(ROCR)par(mfrow=c(1, 2))prediction(test.predicted.m1, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()prediction(test.predicted.m2, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()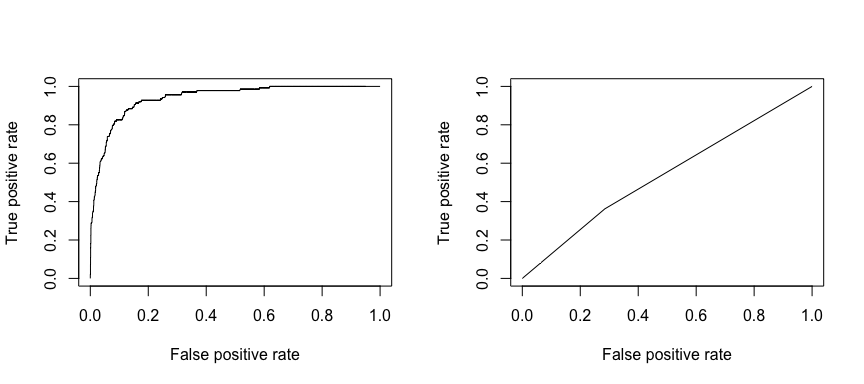

Y para calcular el AUC numéricamente podemos utilizar lo siguiente. Recuerde que el AUC oscilará entre 0,50 y 1,00. Así, el modelo 2 es un modelo clasificador muy pobre mientras que el modelo 1 es un modelo clasificador muy bueno.

# model 1 AUCprediction(test.predicted.m1, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.939932# model 2 AUCprediction(test.predicted.m2, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.5386955

Podemos seguir «afinando» nuestros modelos para mejorar estos índices de clasificación. Si puede mejorar sus curvas AUC y ROC (lo que significa que está mejorando las tasas de precisión de la clasificación) está creando «elevación», lo que significa que está elevando la precisión de la clasificación.

Recursos adicionales

Esto le permitirá ponerse en marcha con la regresión logística. Tenga en cuenta que hay mucho más que usted puede cavar en lo que los siguientes recursos le ayudará a aprender más:

• Una Introducción al Aprendizaje Estadístico
• Modelación Predictiva Aplicada
• Elementos del Aprendizaje Estadístico

.