Când priviți în natură, poate ați observat plante complicate ca acestea:


Această ferigă este formată din multe frunze mici care se ramifică dintr-una mai mare.


Acest broccoli Romanesco este format din conescubesfere mai mici care se învârt în spirală în jurul uneia mai mari.
Inițial, acestea par a fi forme extrem de complexe – dar, când vă uitați mai atent, ați putea observa că ambele urmează un model relativ simplu: toate părțile individuale ale plantelor arată exact la fel ca întreaga plantă, doar că sunt mai mici. Același model se repetă la nesfârșit, la scări mai mici.
În matematică, numim această proprietate autosimilaritate, iar formele care o au se numesc fractali. Ele sunt unele dintre cele mai frumoase și mai bizare obiecte din toată matematica.
Pentru a crea propriile noastre fractale, trebuie să începem cu un model simplu și apoi să îl repetăm la nesfârșit, la scări mai mici.
Unul dintre cele mai simple modele ar putea fi un segment de linie, cu alte două segmente care se ramifică de la un capăt. Dacă repetăm acest model, ambele segmente albastre vor avea, de asemenea, încă două ramificații la capetele lor.
Puteți muta punctele albastre pentru a schimba lungimea și unghiul tuturor ramificațiilor. Apoi creșteți numărul de iterații folosind cursorul de mai jos.
În funcție de poziția ramurilor, puteți realiza modele complet diferite – arătând ca feriga de mai sus, ca un copac sau ca pentagoni imbricați. Ce altceva puteți găsi?
Un alt fractal celebru este triunghiul Sierpinski. În acest caz, începem cu un triunghi mare, echilateral, și apoi tăiem în mod repetat triunghiuri mai mici din părțile rămase.
Observați cum forma finală este alcătuită din trei copii identice ale sale, iar fiecare dintre acestea este alcătuită din copii și mai mici ale întregului triunghi! Ați putea continua să măriți triunghiul la nesfârșit, iar modelele și formele vor continua mereu să se repete.
Plantele de la începutul acestui capitol arată exact ca niște fractali, dar este evident că este imposibil să se creeze fractali adevărați în viața reală. Dacă am continua să repetăm același model la nesfârșit, din ce în ce mai mic, am ajunge în cele din urmă la celule, molecule sau atomi care nu mai pot fi divizați.
Cu toate acestea, folosind matematica, ne putem gândi la proprietățile pe care „ar trebui” să le aibă adevărații fractali – iar acestea sunt foarte surprinzătoare…
Dimensiunile fractalilor
În primul rând, să ne gândim la dimensiunea fractalilor. O linie are dimensiunea . Când o scalăm cu un factor de 2, lungimea ei crește cu un factor de 21=2. Evident!
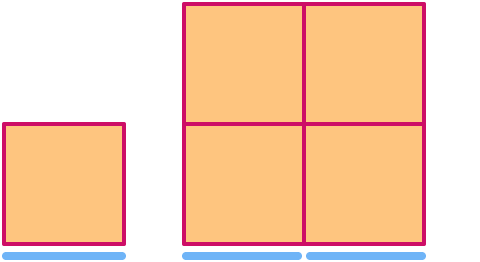
Un pătrat are dimensiunea . La scalarea lui de un factor 2, aria sa crește de un factor 22= .
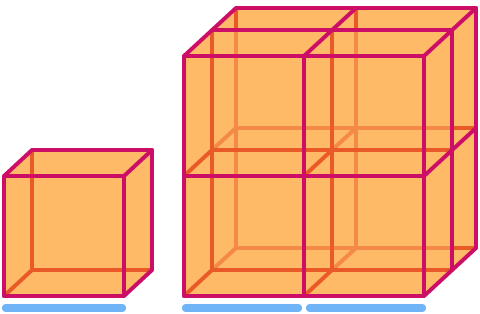
Un cub are dimensiunea . La scalarea lui cu un factor 2, volumul său crește cu un factor 23= . Observați că cubul mai mare din imagine este format din 8 copii ale celui mic!
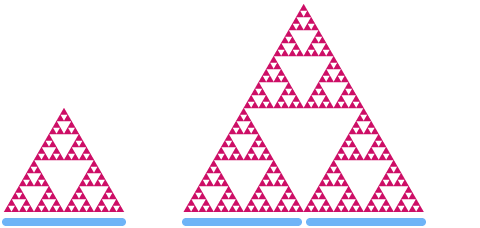
Acum să ne uităm la triunghiul Sierpinski. Dacă îl redimensionăm cu un factor de 2, puteți vedea că „aria” sa crește cu un factor de .
Să spunem că d este dimensiunea triunghiului Sierpinski. Folosind același model ca mai sus, obținem 2d=3. Cu alte cuvinte, d = log23log32 ≈ 1,585…
Dar așteptați… cum poate avea ceva o dimensiune care nu este un număr întreg? Pare imposibil, dar aceasta este doar una dintre proprietățile ciudate ale fractalilor. De fapt, aceasta este ceea ce le dă numele fractalilor: au o dimensiune fracționară.
Cu fiecare iterație, eliminăm o parte din aria triunghiului Sierpinski. Dacă am putea face acest lucru de un număr infinit de ori, nu ar mai rămâne de fapt nicio suprafață: de aceea triunghiul Sierpinski este ceva între o suprafață bidimensională și o linie unidimensională.
În timp ce multe fractale sunt autosimilare, o definiție mai bună este aceea că fractalele sunt forme care au o dimensiune non-integrală.
Fulgul de zăpadă Koch
Există multe forme în natură care arată ca niște fractale. Am văzut deja câteva plante la începutul acestui capitol. Alte exemple minunate sunt fulgii de zăpadă și cristalele de gheață:
Pentru a crea propriul nostru fulg de zăpadă fractal, trebuie din nou să găsim o procedură simplă pe care să o putem aplica la nesfârșit.
Ca și în cazul triunghiului Sierpinski, să începem cu un singur triunghi echilateral. Totuși, în loc să eliminăm triunghiuri mai mici la fiecare pas, adăugăm triunghiuri mai mici de-a lungul marginii. Lungimea laterală a fiecărui triunghi este 131412 din triunghiurile din pasul anterior.
Forma rezultată se numește fulgul de zăpadă Koch, după numele matematicianului suedez Helge von Koch. Observați, încă o dată, că secțiunile mici ale marginii fulgului de zăpadă arată exact la fel ca secțiunile mai mari.
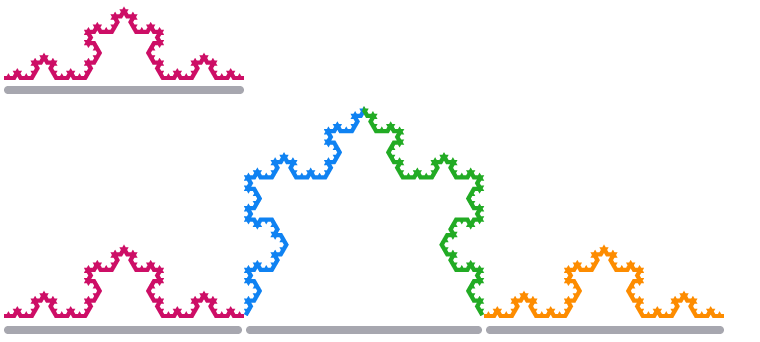
Când redimensionăm un segment de margine al fulgului de zăpadă Koch cu un factor de 3, lungimea acestuia se cvadruplează.
Folosind aceeași relație între dimensiuni și factori de scară ca mai sus, obținem ecuația 3d=42d=42d=34d=3. Aceasta înseamnă că dimensiunea fulgului de zăpadă Koch este d=log34≈1,262.
Arie
Crearea fulgilor de zăpadă Koch este aproape ca o secvență recursivă: cunoaștem forma de pornire (un triunghi) și știm cum să ajungem de la un termen la altul (adăugând mai multe triunghiuri pe fiecare muchie):


triunghiuri noi

triunghiuri noi

triunghiuri noi
După prima iterație, numărul de triunghiuri noi adăugate crește cu un factor de la fiecare pas. În același timp, aria acestor noi triunghiuri scade cu un factor de la fiecare pas.
Să presupunem că primul triunghi are o arie de 1. Atunci aria totală a următoarelor trei triunghiuri este 3×19=13. Următorii pași formează toți o serie geometricăserie aritmeticăserie pătratică, cu raportul comun 499443.
Folosind formula pentru suma seriilor geometrice infinite, putem calcula că aria totală a fulgului de zăpadă Koch este
A=1+13×11-491+949-14=85=1.6.
Perimetrul
De asemenea, putem încerca să calculăm și perimetrul fulgului de zăpadă Koch. După cum am văzut deja înainte, lungimea perimetrului se schimbă cu un factor de 433414 la fiecare pas.
Aceasta înseamnă că, din nou, avem o serie geometrică – dar în acest caz, ea nu convergeconverge la 0nu are un prim termen. Aceasta înseamnă că perimetrul fulgului de zăpadă Koch este de fapt infinit de lung!

Dacă acest lucru pare contraintuitiv, amintiți-vă că înmulțim perimetrul cu 43 la fiecare pas, și facem acest lucru de infinit de multe ori.
Este aproape de neconceput că poți avea o formă cu o arie finită și, de asemenea, cu o circumferință infinită – dar aceasta este doar una dintre multele proprietăți neașteptate ale fractalilor.
Vă puteți gândi la alte modalități de a vă crea propriile fractale?
„Sufletul meu se învârte în spirală pe fractale înghețate de jur împrejur…”
Menger Sponge
Fractalele nu trebuie să fie „plate”, ca multe dintre exemplele de mai sus. Unul dintre cei mai faimoși fractali care au un aspect tridimensional este buretele Menger, numit după matematicianul Karl Menger care l-a descris pentru prima dată în 1926.
Începem cu un cub solid și facem în mod repetat găuri din ce în ce mai mici în laturile sale. Fiecare nouă iterație de găuri are 131214 lățimea iterației anterioare de găuri.
Un cub 3×3×3 este format din 27 de cuburi mai mici, dar aici am eliminat o parte dintre acestea. Buretele lui Menger este format din copii ale lui însuși, care sunt de 3 ori mai mici.
Acum putem încerca să calculăm dimensiunea d a buretelui lui Menger la fel cum am făcut pentru fulgul de zăpadă Koch de mai sus. În acest caz obținem 3d=20, sau d=log320≈2,727.
Dacă ne imaginăm că am tăia din ce în ce mai multe găuri, de un număr infinit de ori, nu ar mai rămâne niciun volum real. Iată de ce cubul nu este „chiar” tridimensional!
Liniile de coastă fractale
Una dintre caracteristicile cheie ale tuturor fractalilor pe care i-am văzut până acum este că poți „mări” la nesfârșit și poți găsi mereu modele noi. În jurul anului 1920, matematicianul britanic Lewis Fry Richardson și-a dat seama că același lucru este valabil și pentru granița sau linia de coastă a multor țări.
Începi cu forma de bază a țării și, pe măsură ce faci zoom, adaugi intrări de râuri, golfuri și estuare, apoi faleze individuale, stânci, pietricele și așa mai departe:
Aceasta este o problemă semnificativă atunci când încerci să calculezi lungimea graniței unei țări – cum decizi cât de mult să faci zoom in și ce colțuri și colțișoare să incluzi?
Un mod în care am putea măsura lungimea liniei de coastă a Marii Britanii, de exemplu, este să luăm o riglă lungă, să ne plimbăm în jurul plajelor sale și apoi să adunăm toate distanțele.
Dacă riglă are o lungime de ${rulă}km, trebuie să o folosim de ${număr} ori, astfel încât să obținem o linie de coastă totală de ${număr} × ${rulers} = ${count * rulers}km.
Putem continua, cu rigle din ce în ce mai mici, și de fiecare dată rezultatul pentru lungimea liniei de coastă va fi un pic mai lung. La fel ca în cazul fulgului de zăpadă Koch de mai devreme, se pare că linia de coastă a Marii Britanii este infinit de lungă! Acest lucru este adesea numit paradoxul liniei de coastă.
Câteva decenii mai târziu, matematicianul Benoit Mandelbrot a dat peste lucrarea lui Richardson într-o carte de bibliotecă aruncată la gunoi, în timp ce lucra la IBM. El a recunoscut importanța acesteia și, de asemenea, modul în care se leagă de cercetările mai recente privind fractalii și dimensiunile.
Linia de coastă a Marii Britanii cu siguranță „pare” fractală, dar nu este autosimilară, ca alte fractale pe care le-am văzut înainte. Pentru a-i afla dimensiunea, o putem desena pe o grilă și număra numărul de celule cu care se intersectează.
Inițial, există 88 de celule care se intersectează. Dacă mărim linia de coastă cu un factor 2, există 197 de celule care se intersectează – mai mult de două ori mai multe!
Dimensiunea liniei de coastă a crescut de un factor de 19788. Ca și înainte, acest lucru înseamnă că dimensiunea liniei de coastă este
d=log219788≈1,16
Dacă am repeta acest lucru cu grile mai mari, am descoperi că dimensiunea liniei de coastă a Marii Britanii este de fapt de aproximativ 1,21. Mandelbrot și-a dat seama că această dimensiune fractală este, de asemenea, o măsură a rugozității unei forme – un concept nou, pentru care a găsit aplicații importante în multe alte domenii ale matematicii și științei.
Mai multe fractale în natură și tehnologie
În timp ce adevăratele fractale nu pot apărea niciodată în natură, există multe obiecte care arată aproape ca niște fractale. Am văzut deja plante, fulgi de zăpadă și linii de coastă, și iată alte câteva exemple:
Lanț muntos în Asia Centrală
Delta fluviului Gange în India
Fulgere
. Vasele de sânge din retină
Marele Canion din SUA
Nori
Toate aceste obiecte ar putea părea complet aleatorii, dar, la fel ca în cazul fractalilor, există un model de bază care determină modul în care sunt formate. Matematica ne poate ajuta să înțelegem mai bine aceste forme, iar fractalii au aplicații în domenii precum medicina, biologia, geologia și meteorologia.
Teren fractal generat pe calculator
De asemenea, putem folosi fractalii pentru a crea „copii” realiste ale naturii, de exemplu, ca peisaje și texturi folosite în jocurile video sau în filmele generate pe calculator. Apa, munții și norii din această imagine sunt creați în întregime de un computer, cu ajutorul fractalilor!
Și putem chiar inversa acest proces pentru a comprima imaginile digitale, pentru a le reduce dimensiunea fișierului. Primii algoritmi au fost dezvoltați de Michael Barnsley și Alan Sloan în anii 1980, iar noi algoritmi sunt cercetați și astăzi.
.