Encuentras factoriales por toda la combinatoria porque es ahí donde se originaron. El factorial se creó como una forma de expresar el número de arreglos de un grupo de elementos, que por supuesto encontramos utilizando, en su forma más básica, la regla de multiplicación del conteo.
El factorial es una especie de operación no oficial de la regla de multiplicación del conteo.
Por qué el factorial cero es igual a 1
Aquí es donde se pone complicado porque si sólo pensamos en los factoriales en el contexto en el que se suelen definir, es decir.es decir, el «producto de todos los enteros positivos menores o iguales que el número», entonces averiguar el 0! es como chocar con una pared de ladrillos.
La mayoría de la gente te dirá que el 0! está definido como 1, y si preguntas por qué sólo te dicen «porque está definido como uno».
Sí, es bastante frustrante. Es el equivalente matemático a preguntar a tus padres por qué tienes que seguir una regla arbitraria que se han inventado y que te digan «porque lo digo yo».
Aunque esa pueda ser una técnica de crianza aceptada, es una forma pésima de aprender matemáticas. Entonces, ¿cuál es el problema? ¿Cómo decidimos que el factorial cero es igual a uno?
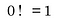
Una comprensión intuitiva
¿Recuerdas que dijimos que el factorial se originaba en la operación matemática de encontrar el número de permutaciones o arreglos de un conjunto? (Nota: no las permutaciones de un conjunto menor a partir de un conjunto mayor, sino simplemente los arreglos de un conjunto dado.)
El factorial cero puede pensarse como el número de arreglos de elementos cero en un conjunto, también conocido como el conjunto vacío {}. (Si alguna vez has estudiado conjuntos, quizás en estadística básica o en matemáticas discretas, probablemente estés familiarizado con el concepto de conjunto vacío. Es, literalmente, el conjunto de la nada.)
Ahora bien, si te preguntara cuántos arreglos hay de una cosa, responderías 1 porque sólo hay una forma de arreglar una cosa. Aquí se sigue la misma idea. Nuestra «única cosa» es el conjunto vacío, y el número de arreglos del conjunto vacío es uno. Eso es todo. Por eso, ¡0! es igual a 1.
Cómo simplificar expresiones factoriales
Ahora que tenemos los fundamentos detrás de nosotros es el momento para el corazón de nuestro tutorial factorial: simplificar.
La mejor manera de ver las matemáticas es en acción. Así que aquí estoy para guiarte a través de los seis problemas que se muestran en la imagen de la parte superior de este post. Empezaremos de forma sencilla, luego pasaremos a la fórmula de combinaciones con números y luego con variables, y terminaremos con algunas expresiones factoriales más complicadas.
❤ ESTÁ CONECTADO ❤
¡No te pierdas ni un problema matemático!