Som en enkel harmonisk rörelse
Vid en block som är fäst vid en fjäder på ett friktionsfritt bord (figur \(\PageIndex{3}\)). Jämviktsläget (det läge där fjädern varken sträcks eller trycks ihop) är markerat som x = 0 . I jämviktsläget är nettokraften noll.
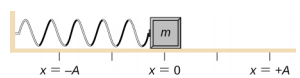
Blockets arbete utförs för att dra ut det till ett läge x = + A, och det släpps sedan från viloläget. Det maximala x-läget (A) kallas rörelsens amplitud. Blocket börjar svänga i SHM mellan x = + A och x = -A, där A är rörelsens amplitud och T är svängningens period. Perioden är tiden för en svängning. Figur \(\PageIndex{4}\) visar blockets rörelse när det fullbordar en och en halv svängning efter frisläppandet.
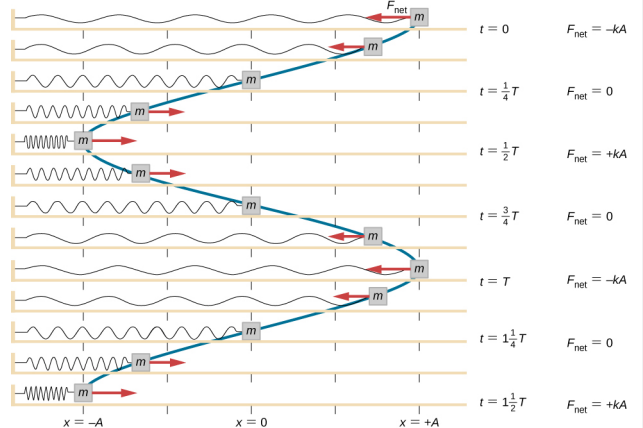
\
Ekvationen för positionen som en funktion av tiden \(x(t) = A\cos( \omega t)\) är bra för modellering av data, där klossens position vid den initiala tiden t = 0,00 s är vid amplituden A och den initiala hastigheten är noll. Ofta när man tar experimentella data är massans position vid den inledande tiden t = 0,00 s inte lika med amplituden och den inledande hastigheten är inte noll. Tänk på 10 sekunders data som samlats in av en elev i labbet och som visas i figur \(\PageIndex{6}\).
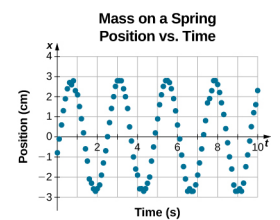
Data i figur \(\PageIndex{6}\) kan fortfarande modelleras med en periodisk funktion, som en cosinusfunktion, men funktionen är förskjuten till höger. Denna förskjutning kallas fasförskjutning och representeras vanligtvis av den grekiska bokstaven phi (\(\phi\)). Ekvationen för positionen som en funktion av tiden för ett block på en fjäder blir
\
Detta är den generaliserade ekvationen för SHM där t är tiden mätt i sekunder, \(\omega\) är vinkelfrekvensen med enheterna inversa sekunder, A är amplituden mätt i meter eller centimeter, och \(\phi\) är fasförskjutningen mätt i radianer (Figur \(\PageIndex{7}\)). Det bör noteras att eftersom sinus- och cosinusfunktionerna endast skiljer sig åt genom en fasförskjutning, kan denna rörelse modelleras med hjälp av antingen cosinus- eller sinusfunktionen.
Hastigheten för massan på en fjäder, som oscillerar i SHM, kan hittas genom att ta derivatan av positionsekvationen:
\
Då sinusfunktionen oscillerar mellan -1 och +1, är den maximala hastigheten amplituden gånger vinkelfrekvensen, vmax = A\(\omega\). Den maximala hastigheten inträffar i jämviktsläget (x = 0) när massan rör sig mot x = + A. Den maximala hastigheten i negativ riktning uppnås i jämviktsläget (x = 0) när massan rör sig mot x = -A och är lika med -vmax.
Massans acceleration på fjädern kan hittas genom att ta tidsderivatan av hastigheten:
\\