Beräkning av ΔS från termodynamiska cykler
Vi kan också beräkna en entropiförändring med hjälp av en termodynamisk cykel. Som du lärde dig tidigare är den molära värmekapaciteten (Cp) den mängd värme som behövs för att höja temperaturen på 1 mol av ett ämne med 1 °C vid konstant tryck. På samma sätt är Cv den värmemängd som behövs för att höja temperaturen hos 1 mol av ett ämne med 1 °C vid konstant volym. Ökningen av entropin med ökande temperatur i figur \(\PageIndex{2}\) är ungefär proportionell mot ämnets värmekapacitet.
Håll dig i minnet att entropiförändringen (ΔS) är relaterad till värmeströmningen (qrev) genom ΔS = qrev/T. Eftersom qrev = nCpΔT vid konstant tryck eller nCvΔT vid konstant volym, där n är antalet mol av det närvarande ämnet, är entropiförändringen för ett ämne vars temperatur ändras från T1 till T2 följande:
\
Som du kommer att upptäcka i mer avancerade matematikkurser än vad som krävs här, kan man visa att detta är lika med följande:För en genomgång av naturliga logaritmer, se grundläggande färdigheter 6 i kapitel 11 ”Vätska”.
\
Samma sak,
\
Därmed kan vi använda en kombination av mätningar av värmekapaciteten (ekvation 18.20 eller ekvation 18.21) och experimentellt uppmätta värden på fusions- eller förångningsenthalpier om det är fråga om en fasförändring (ekvation 18.18) för att beräkna entropiförändringen som motsvarar en temperaturförändring hos ett prov.
Vi kan använda en termodynamisk cykel för att beräkna entropiförändringen när fasförändringen för ett ämne som svavel inte kan mätas direkt. Som noterades i övningen i exempel 6 finns elementärt svavel i två former (del (a) i figur \(\PageIndex{3}\)): en ortorhombisk form med en mycket ordnad struktur (Sα) och en mindre ordnad monoklin form (Sβ). Den ortorhombiska (α) formen är mer stabil vid rumstemperatur men genomgår en fasövergång till den monokliniska (β) formen vid temperaturer högre än 95,3°C (368,5 K). Övergången från Sα till Sβ kan beskrivas av den termodynamiska cykel som visas i del (b) i figur \(\PageIndex{3}\), där flytande svavel är en intermediär. Den entropiförändring som följer med omvandlingen av flytande svavel till Sβ (-ΔSfus(β) = ΔS3 i cykeln) kan inte mätas direkt. Eftersom entropin är en tillståndsfunktion kan ΔS3 dock beräknas från den totala entropiförändringen (ΔSt) för Sα-Sβ-övergången, som är lika med summan av ΔS-värdena för stegen i den termodynamiska cykeln, med hjälp av ekvation 18.20 och tabellerade termodynamiska parametrar (värmekapaciteten för Sα och Sβ, ΔHfus(α), och smältpunkten för Sα.)

Lösning för ΔS3 ger ett värde på -3,24 J/(mol-K). Som förväntat för omvandlingen av ett mindre ordnat tillstånd (en vätska) till ett mer ordnat (en kristall) är ΔS3 negativt.
Hur mäts entropier
Den absoluta entropin hos en substans vid en temperatur över 0 K måste bestämmas genom att beräkna de ökningar av värme q som krävs för att föra substansen från 0 K till den temperatur som är av intresse, och sedan summera förhållandena q/T. Två typer av experimentella mätningar behövs:
- De entalper som är förknippade med eventuella fasförändringar som ämnet kan genomgå inom det aktuella temperaturområdet. Smältning av ett fast ämne och förångning av en vätska motsvarar betydande ökningar av antalet mikrotillstånd som är tillgängliga för att ta emot termisk energi, så när dessa processer inträffar kommer energi att strömma in i ett system och fylla dessa nya mikrotillstånd i den utsträckning som krävs för att upprätthålla en konstant temperatur (fryspunkten eller kokpunkten); dessa inflöden av termisk energi motsvarar fusions- och förångningsvärmen. Entropiökningen i samband med smältning är till exempel bara ΔHfusion/Tm.
- Värmekapaciteten C hos en fas uttrycker den värmemängd som krävs för att ändra temperaturen med en liten mängd ΔT , eller närmare bestämt, med en infinitesimal mängd dT . Den entropiökning som åstadkoms genom uppvärmning av ett ämne över ett temperaturintervall som inte omfattar en fasövergång ges således av summan av kvantiteterna C dT/T för varje temperaturökning dT . Detta är naturligtvis bara integralen
\
Eftersom värmekapaciteten i sig själv är något temperaturberoende, kräver de mest exakta bestämningarna av absoluta entropier att C:s funktionella beroende av T används i ovanstående integral i stället för en konstant C.
\
När detta inte är känt kan man göra en serie mätningar av värmekapaciteten över snäva temperatursteg ΔT och mäta arean under varje avsnitt av kurvan.
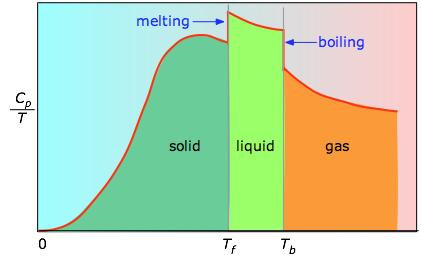
Utbredningen under varje sektion i diagrammet representerar entropiförändringen som är förknippad med uppvärmning av ämnet genom ett intervall ΔT. Till detta måste läggas entalpen för smältning, förångning och eventuella fasförändringar mellan fast och fast substans. Värden av Cp för temperaturer nära noll mäts inte direkt, men kan uppskattas från kvantteori.
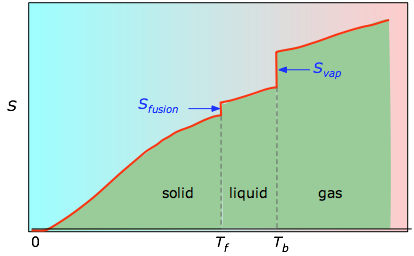
De kumulativa ytorna från 0 K till en given temperatur (hämtade från den experimentella plotten till vänster) plottas sedan som en funktion av T, och eventuella fasförändringsentropier som Svap = Hvap / Tb adderas för att erhålla den absoluta entropin vid temperaturen T.