Den logistiska ekvationen (ibland kallad Verhulst-modellen eller logistisk tillväxtkurva) är en modell för befolkningstillväxt som först publicerades av Pierre Verhulst (1845, 1847). Modellen är kontinuerlig i tid, men en modifiering av den kontinuerliga ekvationen till en diskret kvadratisk återkommande ekvation som kallas logistisk karta används också ofta.
Den kontinuerliga versionen av den logistiska modellen beskrivs av differentialekvationen
 |
(1)
|
där 
är den malthusianska parametern (hastigheten för den maximala befolkningstillväxten) och 
är den s.k. bärkraft (dvs, den maximala hållbara befolkningen). Genom att dividera båda sidorna med 
och definiera 
får man sedan differentialekvationen
 |
(2)
|
som är känd. som den logistiska ekvationen och har lösningen
 |
(3)
|
Funktionen 
är ibland känd som sigmoidfunktionen.
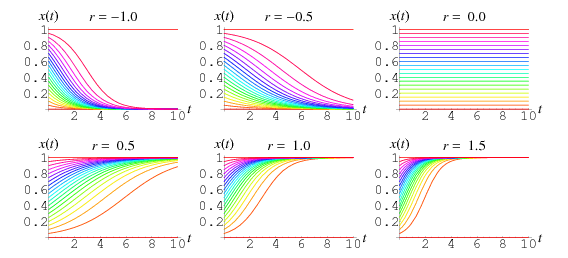
Om 
vanligen begränsas till att vara positiv, visas diagram för ovanstående lösning för olika positiva och negativa värden på 
och initialvillkor 
som sträcker sig från 0,00 till 1,00 i steg om 0,05.
Den diskreta versionen av den logistiska ekvationen (3) är känd som den logistiska kartan.
Kurvan
 |
(4)
|
som erhålls från (3) är ibland känd som den logistiska kurvan. På samma sätt används vanligen en normaliserad form av ekvation (3) som en statistisk fördelning som kallas logistisk fördelning.