Logistisk regression

Logistisk regression (även kallad logitregression eller logitmodell) utvecklades av statistikern David Cox 1958 och är en regressionsmodell där responsvariabeln Y är kategorisk. Logistisk regression gör det möjligt att uppskatta sannolikheten för ett kategoriskt svar baserat på en eller flera prediktorvariabler (X). Det gör det möjligt att säga att närvaron av en prediktor ökar (eller minskar) sannolikheten för ett visst resultat med en viss procentsats. Den här handledningen täcker fallet när Y är binär – det vill säga när den endast kan anta två värden, ”0” och ”1”, som representerar utfall såsom godkänt/underkänt, vinner/förlorar, levande/död eller frisk/sjuk. Fall där den beroende variabeln har mer än två utfallskategorier kan analyseras med multinomial logistisk regression eller, om de flera kategorierna är ordnade, med ordinal logistisk regression. Diskriminantanalys har dock blivit en populär metod för klassificering av flera klasser, så vår nästa handledning kommer att fokusera på den tekniken för dessa fall.

tl;dr

Denna handledning fungerar som en introduktion till logistisk regression och täcker1:

1. Replikeringskrav: Vad du behöver för att reproducera analysen i denna handledning
2. Varför logistisk regression: Varför använda logistisk regression?
3. Förberedelse av våra data: Förbered våra data för modellering
4. Enkel logistisk regression: Förutsägelse av sannolikheten för svaret Y med en enda prediktorvariabel X
5. Multipel logistisk regression: Logistisk regression:
6. Modellutvärdering & Diagnostik: Hur väl passar modellen in på data? Vilka prediktorer är viktigast? Är förutsägelserna korrekta?

Replikeringskrav

Denna handledning utnyttjar i första hand Default-data som tillhandahålls av paketet ISLR. Detta är en simulerad datamängd som innehåller information om tiotusen kunder, t.ex. om kunden har försummat sina betalningar, om kunden är student, kundens genomsnittliga saldo och kundens inkomst. Vi kommer också att använda några paket som tillhandahåller datamanipulering, visualisering, funktioner för pipeline-modellering och funktioner för att städa upp modellresultatet.

# Packageslibrary(tidyverse) # data manipulation and visualizationlibrary(modelr) # provides easy pipeline modeling functionslibrary(broom) # helps to tidy up model outputs# Load data (default <- as_tibble(ISLR::Default))## # A tibble: 10,000 × 4## default student balance income## <fctr> <fctr> <dbl> <dbl>## 1 No No 729.5265 44361.625## 2 No Yes 817.1804 12106.135## 3 No No 1073.5492 31767.139## 4 No No 529.2506 35704.494## 5 No No 785.6559 38463.496## 6 No Yes 919.5885 7491.559## 7 No No 825.5133 24905.227## 8 No Yes 808.6675 17600.451## 9 No No 1161.0579 37468.529## 10 No No 0.0000 29275.268## # ... with 9,990 more rows

Varför logistisk regression

Linjär regression är inte lämplig när det gäller ett kvalitativt svar. Varför inte? Anta att vi försöker förutsäga det medicinska tillståndet hos en patient på akutmottagningen utifrån hennes symtom. I detta förenklade exempel finns det tre möjliga diagnoser: stroke, överdosering av läkemedel och epileptiskt anfall. Vi kan överväga att koda dessa värden som en kvantitativ svarsvariabel, Y , enligt följande:

Med hjälp av denna kodning kan minsta kvadratmetoden användas för att anpassa en linjär regressionsmodell för att förutsäga Y på grundval av en uppsättning prediktorer . Tyvärr innebär denna kodning en ordningsföljd för resultaten, genom att placera överdosering av läkemedel mellan stroke och epileptiskt anfall och insistera på att skillnaden mellan stroke och överdosering av läkemedel är densamma som skillnaden mellan överdosering av läkemedel och epileptiskt anfall. I praktiken finns det inget särskilt skäl till att detta måste vara fallet. Man skulle till exempel kunna välja en lika rimlig kodning,

som skulle innebära ett helt annat förhållande mellan de tre tillstånden. Var och en av dessa kodningar skulle ge fundamentalt olika linjära modeller som i slutändan skulle leda till olika uppsättningar av förutsägelser om testobservationer.

Mer relevant för våra data, om vi försöker klassificera en kund som en kund med hög respektive låg risk för betalningsinställelse på grundval av deras saldo skulle vi kunna använda linjär regression; den vänstra figuren nedan illustrerar dock hur linjär regression skulle förutsäga sannolikheten för betalningsinställelse. Tyvärr förutsäger vi för saldon nära noll en negativ sannolikhet för betalningsinställelse; om vi skulle förutsäga för mycket stora saldon skulle vi få värden som är större än 1. Dessa förutsägelser är inte förnuftiga, eftersom den verkliga sannolikheten för betalningsinställelse, oavsett kreditkortsaldo, naturligtvis måste ligga mellan 0 och 1.

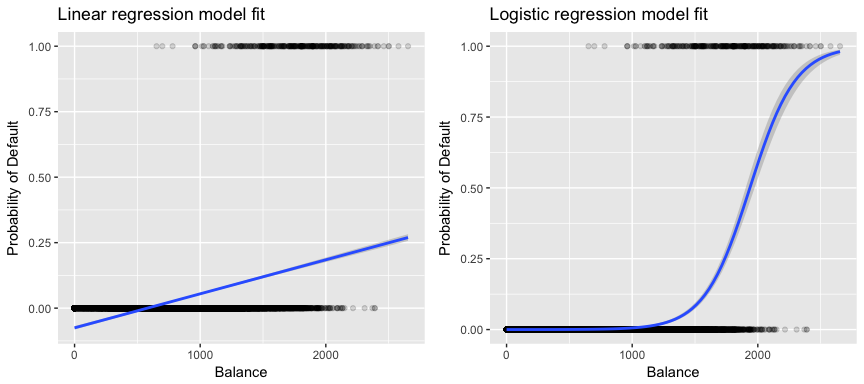
För att undvika detta problem måste vi modellera p(X) med hjälp av en funktion som ger utdata mellan 0 och 1 för alla värden på X. Många funktioner uppfyller denna beskrivning. I logistisk regression använder vi den logistiska funktionen, som definieras i Eq. 1 och illustreras i den högra figuren ovan.

Förberedelse av våra data

Som i regressionshandledningen kommer vi att dela upp våra data i en träningsuppsättning (60 %) och en testuppsättning (40 %), så att vi kan bedöma hur väl vår modell fungerar på en datauppsättning utanför urvalet.

set.seed(123)sample <- sample(c(TRUE, FALSE), nrow(default), replace = T, prob = c(0.6,0.4))train <- defaulttest <- default

Enklare logistisk regression

Vi kommer att anpassa en logistisk regressionsmodell för att förutsäga sannolikheten för att en kund ska bli betalningsinställd baserat på det genomsnittliga saldot som kunden har. Funktionen glm anpassar generaliserade linjära modeller, en klass av modeller som inkluderar logistisk regression. Syntaxen för glm-funktionen liknar syntaxen för lm, förutom att vi måste lämna över argumentet family = binomial för att tala om för R att köra en logistisk regression i stället för någon annan typ av generaliserad linjär modell.

model1 <- glm(default ~ balance, family = "binomial", data = train)

I bakgrunden använder glm, maximum likelihood för att anpassa modellen. Den grundläggande intuitionen bakom att använda maximal sannolikhet för att anpassa en logistisk regressionsmodell är följande: vi söker skattningar för och så att den förutspådda sannolikheten för betalningsinställelse för varje individ, med hjälp av ekv. 1, motsvarar så nära som möjligt individens observerade status för betalningsinställelse. Med andra ord försöker vi hitta och på ett sådant sätt att om vi sätter in dessa skattningar i modellen för p(X), som ges i Eq. 1, får vi ett tal nära ett för alla individer som inte betalade sina skulder och ett tal nära noll för alla individer som inte betalade sina skulder. Denna intuition kan formaliseras med hjälp av en matematisk ekvation som kallas sannolikhetsfunktion:

Skattningarna och väljs för att maximera denna sannolikhetsfunktion. Maximal sannolikhet är ett mycket allmänt tillvägagångssätt som används för att anpassa många av de icke-linjära modeller som vi kommer att undersöka i framtida handledningar. Resultatet blir en S-formad sannolikhetskurva som illustreras nedan (observera att för att kunna plotta den logistiska regressionens anpassningslinje måste vi omvandla vår svarsvariabel till en binärt kodad variabel).

default %>% mutate(prob = ifelse(default == "Yes", 1, 0)) %>% ggplot(aes(balance, prob)) + geom_point(alpha = .15) + geom_smooth(method = "glm", method.args = list(family = "binomial")) + ggtitle("Logistic regression model fit") + xlab("Balance") + ylab("Probability of Default")

Som vid linjär regression kan vi utvärdera modellen med hjälp av summary eller glance. Observera att formatet för koefficientutmatningen liknar det vi såg i linjär regression, men detaljerna om goodness-of-fit längst ned i summary skiljer sig åt. Vi kommer att gå in mer på detta senare men notera bara att du ser ordet avvikelse. Avvikelse är analogt med summan av kvadratberäkningar i linjär regression och är ett mått på bristen på anpassning till data i en logistisk regressionsmodell. Nollavvikelsen representerar skillnaden mellan en modell med endast interceptet (vilket innebär ”inga prediktorer”) och en mättad modell (en modell med en teoretiskt sett perfekt anpassning). Målet är att modellavvikelsen (noterad som Residualavvikelse) ska vara lägre; mindre värden tyder på bättre anpassning. I detta avseende ger nollmodellen en baslinje som man kan jämföra prediktormodeller med.

summary(model1)## ## Call:## glm(formula = default ~ balance, family = "binomial", data = train)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.2905 -0.1395 -0.0528 -0.0189 3.3346 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.101e+01 4.887e-01 -22.52 <2e-16 ***## balance 5.669e-03 2.949e-04 19.22 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 1723.03 on 6046 degrees of freedom## Residual deviance: 908.69 on 6045 degrees of freedom## AIC: 912.69## ## Number of Fisher Scoring iterations: 8

Bedömning av koefficienter

Nedanstående tabell visar koefficientskattningarna och relaterad information som är resultatet av att man anpassar en logistisk regressionsmodell för att förutsäga sannolikheten för att betalningsinställelse = Ja med hjälp av balans. Tänk på att koefficientskattningarna från logistisk regression karaktäriserar förhållandet mellan prediktor- och svarsvariabeln på en log-odds-skala (se kapitel 3 i ISLR1 för mer information). Vi ser alltså att ; detta tyder på att en ökning av saldot är förknippad med en ökning av sannolikheten för betalningsinställelse. För att vara exakt, en ökning av saldot med en enhet är förknippad med en ökning av log oddset för betalningsinställelse med 0,0057 enheter.

tidy(model1)## term estimate std.error statistic p.value## 1 (Intercept) -11.006277528 0.488739437 -22.51972 2.660162e-112## 2 balance 0.005668817 0.000294946 19.21985 2.525157e-82

Vi kan vidare tolka saldokoefficienten som – för varje dollar ökning av det månatliga saldot som bärs ökar oddset för att kunden ska bli betalningsinställd med en faktor 1.0057.

exp(coef(model1))## (Intercept) balance ## 1.659718e-05 1.005685e+00

Många aspekter av koefficientutmatningen liknar dem som diskuteras i utmatningen för linjär regression. Vi kan till exempel mäta konfidensintervallen och noggrannheten hos koefficientskattningarna genom att beräkna deras standardfel. Till exempel, har ett p-värde < 2e-16 som tyder på ett statistiskt signifikant samband mellan balansräkningen och sannolikheten för betalningsinställelse. Vi kan också använda standardfelen för att få fram konfidensintervall som vi gjorde i handledningen om linjär regression:

confint(model1)## 2.5 % 97.5 %## (Intercept) -12.007610373 -10.089360652## balance 0.005111835 0.006269411

Förutsägelser

När koefficienterna har uppskattats är det enkelt att beräkna sannolikheten för betalningsinställelse för ett givet kreditkortsaldo. Matematiskt sett kan vi med hjälp av koefficientskattningarna från vår modell förutsäga att sannolikheten för betalningsinställelse för en person med ett saldo på 1 000 dollar är mindre än 0,5 %

Vi kan förutsäga sannolikheten för betalningsinställelse i R med hjälp av funktionen predict (se till att inkludera type = "response"). Här jämför vi sannolikheten för betalningsinställelse baserat på saldon på 1 000 dollar och 2 000 dollar. Som du kan se när saldot går från 1 000 dollar till 2 000 dollar ökar sannolikheten för betalningsinställelse markant, från 0,5 % till 58 %!

predict(model1, data.frame(balance = c(1000, 2000)), type = "response")## 1 2 ## 0.004785057 0.582089269

Man kan också använda kvalitativa prediktorer med den logistiska regressionsmodellen. Som exempel kan vi anpassa en modell som använder variabeln student.

model2 <- glm(default ~ student, family = "binomial", data = train)tidy(model2)## term estimate std.error statistic p.value## 1 (Intercept) -3.5534091 0.09336545 -38.05914 0.000000000## 2 studentYes 0.4413379 0.14927208 2.95660 0.003110511

Koefficienten som är kopplad till student = Yes är positiv och det tillhörande p-värdet är statistiskt signifikant. Detta tyder på att studenter tenderar att ha högre sannolikhet för betalningsinställelse än icke-studenter. Faktum är att denna modell tyder på att en student har nästan dubbelt så hög sannolikhet för betalningsinställelse som icke-studenter. I nästa avsnitt ska vi dock se varför.

predict(model2, data.frame(student = factor(c("Yes", "No"))), type = "response")## 1 2 ## 0.04261206 0.02783019

Multipel logistisk regression

Vi kan också utöka vår modell enligt Eq. 1 så att vi kan förutsäga ett binärt svar med hjälp av flera prediktorer där är p prediktorer:

Låt oss gå vidare och anpassa en modell som förutsäger sannolikheten för betalningsinställelse baserat på variablerna saldo, inkomst (i tusentals dollar) och studentstatus. Det finns ett överraskande resultat här. De p-värden som är förknippade med saldo och student=Yes-status är mycket små, vilket tyder på att var och en av dessa variabler är förknippade med sannolikheten för betalningsinställelse. Koefficienten för studentvariabeln är dock negativ, vilket tyder på att studenter är mindre benägna att ställa in sina betalningar än icke-studenter. Koefficienten för studentvariabeln i modell 2, där vi förutspådde sannolikheten för betalningsinställelse enbart på grundval av studentstatus, visade däremot att studenter har en större sannolikhet för betalningsinställelse. Vad beror det på?

model3 <- glm(default ~ balance + income + student, family = "binomial", data = train)tidy(model3)## term estimate std.error statistic p.value## 1 (Intercept) -1.090704e+01 6.480739e-01 -16.8299277 1.472817e-63## 2 balance 5.907134e-03 3.102425e-04 19.0403764 7.895817e-81## 3 income -5.012701e-06 1.078617e-05 -0.4647343 6.421217e-01## 4 studentYes -8.094789e-01 3.133150e-01 -2.5835947 9.777661e-03

Den högra panelen i figuren nedan ger en förklaring till denna diskrepans. Variablerna student och saldo är korrelerade. Studenter tenderar att ha högre skuldnivåer, vilket i sin tur är förknippat med högre sannolikhet för betalningsinställelse. Med andra ord är studenter mer benägna att ha stora kreditkortsaldon, vilket, som vi vet från den vänstra panelen i figuren nedan, tenderar att vara förknippat med höga betalningsinställelsefrekvenser. Även om en enskild student med ett visst kreditkortsaldo tenderar att ha en lägre sannolikhet för betalningsinställelse än en icke-student med samma kreditkortsaldo, innebär det faktum att studenterna som helhet tenderar att ha högre kreditkortsaldon att studenterna totalt sett tenderar att ha en högre risk för betalningsinställelse än icke-studenter. Detta är en viktig skillnad för ett kreditkortsföretag som försöker avgöra vem de ska erbjuda krediter. En student är mer riskfylld än en icke-student om ingen information om studentens kreditkortsaldo finns tillgänglig. Den studenten är dock mindre riskfylld än en icke-student med samma kreditkortsaldo!

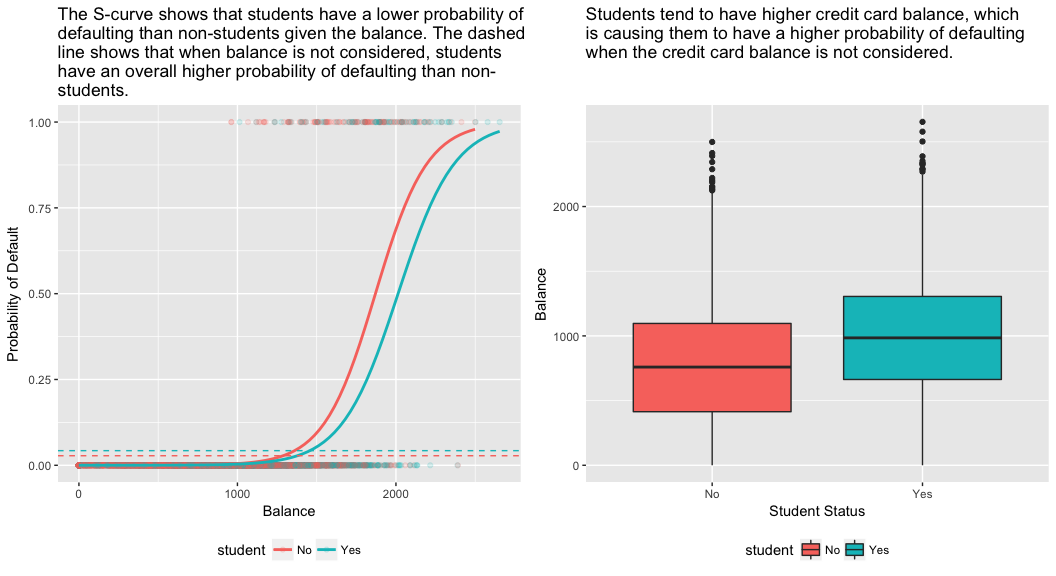
Detta enkla exempel illustrerar de faror och subtiliteter som är förknippade med att utföra regressioner som endast omfattar en enda prediktor när andra prediktorer också kan vara relevanta. De resultat som erhålls med hjälp av en prediktor kan vara helt annorlunda än de som erhålls med hjälp av flera prediktorer, särskilt när det finns en korrelation mellan prediktorerna. Detta fenomen kallas confounding.

I fallet med flera prediktorvariabler vill vi ibland förstå vilken variabel som är mest inflytelserik när det gäller att förutsäga svarsvariabeln (Y). Vi kan göra detta med varImp från paketet caret. Här ser vi att balans är viktigast med stor marginal medan studentstatus är mindre viktig följt av inkomst (som ändå visade sig vara insignifikant (p = .64)).

caret::varImp(model3)## Overall## balance 19.0403764## income 0.4647343## studentYes 2.5835947

Som tidigare kan vi enkelt göra förutsägelser med denna modell. Till exempel har en student med ett kreditkortsaldo på 1 500 dollar och en inkomst på 40 000 dollar en uppskattad sannolikhet för betalningsinställelse på

En icke-student med samma saldo och inkomst har en uppskattad sannolikhet för betalningsinställelse på

new.df <- tibble(balance = 1500, income = 40, student = c("Yes", "No"))predict(model3, new.df, type = "response")## 1 2 ## 0.05437124 0.11440288

Därmed ser vi att för det givna saldot och den givna inkomsten (även om inkomsten är insignifikant) har en student ungefär halva sannolikheten att bli betalningsinställd än en icke-student.

Modellutvärdering &Diagnostik

So långt har tre logistiska regressionsmodeller byggts upp och koefficienterna har undersökts. Några kritiska frågor återstår dock. Är modellerna bra? Hur väl passar modellen in på uppgifterna? Och hur exakta är förutsägelserna på en datamängd utanför stickprovet?

Goodness-of-Fit

I handledningen om linjär regression såg vi hur F-statistik, och justerad , och restdiagnostik informerar oss om hur bra modellen passar in på data. Här ska vi titta på några sätt att bedöma goodness-of-fit för våra logitmodeller.

Likelihood Ratio Test

För det första kan vi använda ett Likelihood Ratio Test för att bedöma om våra modeller förbättrar anpassningen. Att lägga till prediktorvariabler i en modell kommer nästan alltid att förbättra modellanpassningen (dvs. öka loglikelihood och minska modellavvikelsen jämfört med nollavvikelsen), men det är nödvändigt att testa om den observerade skillnaden i modellanpassning är statistiskt signifikant. Vi kan använda anova för att utföra detta test. Resultaten visar att model3, jämfört med model1, minskar residualavvikelsen med över 13 (kom ihåg att ett mål med logistisk regression är att hitta en modell som minimerar residualavvikelsen). Ännu viktigare är att denna förbättring är statistiskt signifikant vid p = 0,001. Detta tyder på att model3 ger en bättre anpassning av modellen.

anova(model1, model3, test = "Chisq")## Analysis of Deviance Table## ## Model 1: default ~ balance## Model 2: default ~ balance + income + student## Resid. Df Resid. Dev Df Deviance Pr(>Chi) ## 1 6045 908.69 ## 2 6043 895.02 2 13.668 0.001076 **## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pseudo

Till skillnad från linjär regression med vanlig skattning av minsta kvadratmetoden finns det ingen statistik som förklarar hur stor del av variansen i den beroende variabeln som förklaras av prediktorerna. Det finns dock ett antal pseudomätetal som kan vara av värde. Den mest anmärkningsvärda är McFaddens , som definieras som

där är loglikelihoodvärdet för den anpassade modellen och är loglikelihoodvärdet för nollmodellen med endast ett intercept som prediktor. Måttet sträcker sig från 0 till strax under 1, med värden närmare noll som anger att modellen inte har någon prediktiv förmåga. Till skillnad från linjär regression uppnår modellerna dock sällan ett högt McFadden-värde. Med McFaddens egna ord representerar modeller med en McFadden-pseudo faktiskt en mycket god anpassning. Vi kan bedöma McFaddens pseudovärden för våra modeller med:

list(model1 = pscl::pR2(model1), model2 = pscl::pR2(model2), model3 = pscl::pR2(model3))## $model1## McFadden ## 0.4726215 ## ## $model2## McFadden ## 0.004898314 ## ## $model3## McFadden ## 0.4805543

Vi ser att modell 2 har ett mycket lågt värde som bekräftar dess dåliga anpassning. Modellerna 1 och 3 har dock mycket högre värden, vilket tyder på att de förklarar en ganska stor del av variansen i standarddata. Dessutom ser vi att modell 3 endast förbättrar den något.

Residualbedömning

Håll i minnet att logistisk regression inte förutsätter att residualerna är normalfördelade eller att variansen är konstant. Avvikelseresterna är dock användbara för att avgöra om enskilda punkter inte passar väl in i modellen. Här kan vi anpassa de standardiserade deviansresidualerna för att se hur många som överstiger 3 standardavvikelser. Först extraherar vi flera användbara bitar av modellresultaten med augment och fortsätter sedan att plotta.

model1_data <- augment(model1) %>% mutate(index = 1:n())ggplot(model1_data, aes(index, .std.resid, color = default)) + geom_point(alpha = .5) + geom_ref_line(h = 3)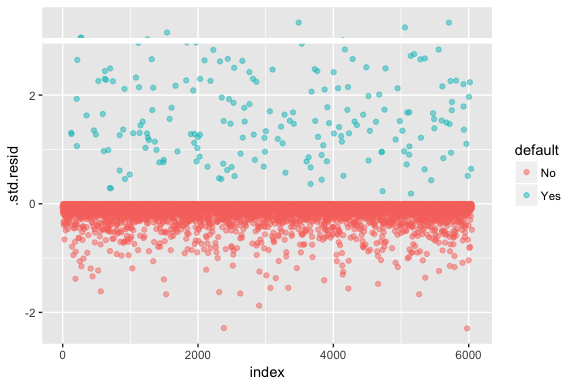

De standardiserade residualer som överstiger 3 representerar möjliga outliers och kan förtjäna närmare uppmärksamhet. Vi kan filtrera efter dessa residualer för att få en närmare granskning. Vi ser att alla dessa observationer representerar kunder som har fallerat med budgetar som är mycket lägre än de normala fallerarna.

model1_data %>% filter(abs(.std.resid) > 3)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 Yes 1118.7010 -4.664566 0.1752745 3.057432 0.0002841609 0.3857438 0.01508609 3.057867 271## 2 Yes 1119.0972 -4.662320 0.1751742 3.056704 0.0002844621 0.3857448 0.01506820 3.057139 272## 3 Yes 1135.0473 -4.571902 0.1711544 3.027272 0.0002967274 0.3857832 0.01435943 3.027721 1253## 4 Yes 1066.8841 -4.958307 0.1885550 3.151288 0.0002463229 0.3856189 0.01754100 3.151676 1542## 5 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 6 Yes 1143.6805 -4.522962 0.1689933 3.011233 0.0003034789 0.3858039 0.01398491 3.011690 4142## 7 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 8 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709

I likhet med linjär regression kan vi också identifiera inflytelserika observationer med Cooks avståndsvärden. Här identifierar vi de fem största värdena.

plot(model1, which = 4, id.n = 5)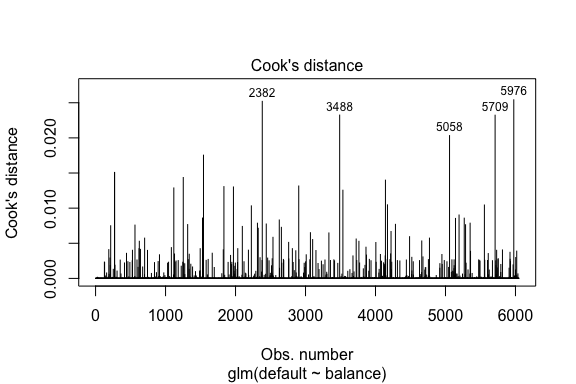

Och vi kan undersöka dessa vidare också. Här ser vi att de fem mest inflytelserika punkterna inkluderar:

• De kunder som blev betalningsinställda med mycket låga saldon och
• Två kunder som inte blev betalningsinställda, men som ändå hade saldon på över 2 000 dollar

Detta innebär att om vi skulle ta bort dessa observationer (inte rekommenderat), skulle formen, läget och konfidensintervallet för vår S-kurva för logistisk regression troligen förändras.

model1_data %>% top_n(5, .cooksd)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 No 2388.1740 2.531843 0.2413764 -2.284011 0.0039757771 0.3866249 0.02520100 -2.288565 2382## 2 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 3 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 4 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709## 5 No 2391.0077 2.547907 0.2421522 -2.290521 0.0039468742 0.3866185 0.02542145 -2.295054 5976

Validering av förutsagda värden

Klassificeringsgrad

När man utvecklar modeller för förutsägelser är det mest kritiska måttet avseende hur väl modellen klarar av att förutsäga målvariabeln på observationer utanför urvalet. Först måste vi använda de uppskattade modellerna för att förutsäga värden på vår träningsdatamängd (train). När du använder predict ska du se till att inkludera type = response så att förutsägelsen returnerar sannolikheten för utfall.

test.predicted.m1 <- predict(model1, newdata = test, type = "response")test.predicted.m2 <- predict(model2, newdata = test, type = "response")test.predicted.m3 <- predict(model3, newdata = test, type = "response")

Nu kan vi jämföra den förutspådda målvariabeln med de observerade värdena för varje modell och se vilken som presterar bäst. Vi kan börja med att använda förvirringsmatrisen, som är en tabell som beskriver klassificeringsprestanda för varje modell på testdata. Varje kvadrant i tabellen har en viktig betydelse. I det här fallet representerar ”Nej” och ”Ja” i raderna huruvida kunderna har fallissemang eller inte. ”FALSK” och ”SANN” i kolumnerna representerar huruvida vi förutspådde att kunderna skulle ställa in sina betalningar eller inte.

• sant positiva (Kvadranten längst ner till höger): Detta är fall där vi förutspådde att kunden skulle ställa in sina betalningar och de gjorde det.
• sant negativa (Kvadranten högst upp till vänster): Vi förutspådde ingen betalningsinställelse och kunden gjorde det inte.
• falska positiva fall (övre högra kvadranten): Detta är fall där vi förutspådde ingen betalningsinställelse och kunden inte gjorde det: Vi förutspådde ja, men kunden blev inte betalningsinställd. (Även känt som ett ”typ I-fel”.)
• falskt negativa (Nedre vänstra kvadranten): Vi förutspådde nej, men de blev faktiskt betalningsinställda. (Även känt som ett ”typ II-fel”.)

Resultaten visar att model1 och model3 är mycket lika varandra. 96 % av de förutspådda observationerna är sant negativa och cirka 1 % är sant positiva. Båda modellerna har ett typ II-fel på mindre än 3 % där modellen förutsäger att kunden inte kommer att ställa in betalningen men att de faktiskt gjorde det. Och båda modellerna har ett typ I-fel på mindre än 1 % där modellerna förutsäger att kunden kommer att ställa in betalningen men aldrig gjorde det. model2 Resultaten skiljer sig markant åt; den här modellen förutsäger exakt de kunder som inte är betalningsinställda (ett resultat av att 97 % av uppgifterna är icke betalningsinställda) men förutsäger aldrig de kunder som är betalningsinställda!

list( model1 = table(test$default, test.predicted.m1 > 0.5) %>% prop.table() %>% round(3), model2 = table(test$default, test.predicted.m2 > 0.5) %>% prop.table() %>% round(3), model3 = table(test$default, test.predicted.m3 > 0.5) %>% prop.table() %>% round(3))## $model1## ## FALSE TRUE## No 0.962 0.003## Yes 0.025 0.010## ## $model2## ## FALSE## No 0.965## Yes 0.035## ## $model3## ## FALSE TRUE## No 0.963 0.003## Yes 0.026 0.009

Vi vill också förstå missklassificerings- (eller fel-) procentsatserna (eller så skulle vi kunna vända på detta och använda det för noggrannhetsprocenterna). Vi ser ingen större förbättring mellan modell 1 och 3, och även om modell 2 har en låg felprocent får man inte glömma att den aldrig korrekt förutsäger kunder som faktiskt inte betalar.

test %>% mutate(m1.pred = ifelse(test.predicted.m1 > 0.5, "Yes", "No"), m2.pred = ifelse(test.predicted.m2 > 0.5, "Yes", "No"), m3.pred = ifelse(test.predicted.m3 > 0.5, "Yes", "No")) %>% summarise(m1.error = mean(default != m1.pred), m2.error = mean(default != m2.pred), m3.error = mean(default != m3.pred))## # A tibble: 1 × 3## m1.error m2.error m3.error## <dbl> <dbl> <dbl>## 1 0.02782697 0.03491019 0.02807994

Vi kan få ytterligare insikter genom att titta på råvärdena (inte procentsatser) i vår förvirringsmatris. Låt oss titta på modell 1 för att illustrera detta. Vi ser att det finns totalt sett ett antal kunder som inte har betalat sina skulder. Av de totala betalningsförsummelserna var inte förutsagda. Alternativt kan vi säga att endast en del av de fallissemang som inträffade förutspåddes – detta kallas modellens precision (även känd som känslighet). Även om den totala felprocenten är låg är precisionen också låg, vilket inte är bra!

table(test$default, test.predicted.m1 > 0.5)## ## FALSE TRUE## No 3803 12## Yes 98 40

Med klassificeringsmodeller kommer man också att använda termerna sensitivitet och specificitet för att beskriva modellens prestanda. Som nämnts ovan är känslighet synonymt med precision. Specificiteten är dock den procentuella andelen icke försumbara personer som identifieras korrekt, här (noggrannheten här styrs till stor del av att 97 % av observationerna i våra data är icke försumbara personer). Betydelsen mellan känslighet och specificitet är beroende av sammanhanget. I det här fallet är det troligt att ett kreditkortsföretag är mer angeläget om känslighet eftersom de vill minska sin risk. Därför kan de vara mer intresserade av att trimma en modell så att deras känslighet/precision förbättras.

Den mottagande operativa karakteristiken (ROC) är ett visuellt mått på klassificerarens prestanda. Genom att använda andelen positiva datapunkter som korrekt betraktas som positiva och andelen negativa datapunkter som felaktigt betraktas som positiva genererar vi en grafisk bild som visar avvägningen mellan den hastighet med vilken man korrekt kan förutsäga något och den hastighet med vilken man felaktigt kan förutsäga något. I slutändan är vi intresserade av arean under ROC-kurvan, eller AUC. Det måttet sträcker sig från 0,50 till 1,00, och värden över 0,80 visar att modellen gör ett bra jobb när det gäller att särskilja mellan de två kategorier som utgör vår målvariabel. Vi kan jämföra ROC- och AUC-värdena för modell 1 och 2, som visar en stark skillnad i prestanda. Vi vill definitivt att våra ROC-plottar ska se mer ut som modell 1:s (vänster) än modell 2:s (höger)!

library(ROCR)par(mfrow=c(1, 2))prediction(test.predicted.m1, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()prediction(test.predicted.m2, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()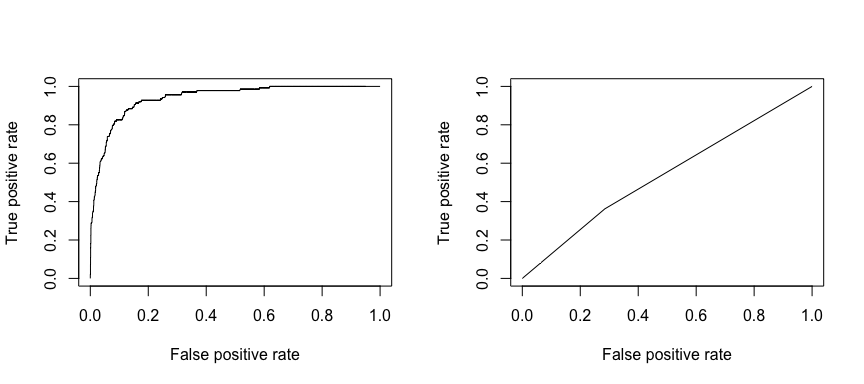

Och för att beräkna AUC numeriskt kan vi använda följande. Kom ihåg att AUC varierar mellan 0,50 och 1,00. Således är modell 2 en mycket dålig klassificeringsmodell medan modell 1 är en mycket bra klassificeringsmodell.

# model 1 AUCprediction(test.predicted.m1, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.939932# model 2 AUCprediction(test.predicted.m2, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.5386955

Vi kan fortsätta att ”trimma” våra modeller för att förbättra dessa klassificeringstal. Om du kan förbättra dina AUC- och ROC-kurvor (vilket innebär att du förbättrar klassificeringsnoggrannheten) skapar du ett ”lyft”, vilket innebär att du lyfter klassificeringsnoggrannheten.

Att ytterligare resurser

Detta kommer att hjälpa dig att komma igång med logistisk regression. Tänk på att det finns mycket mer du kan gräva i så följande resurser hjälper dig att lära dig mer:

• An Introduction to Statistical Learning
• Applied Predictive Modeling
• Elements of Statistical Learning