I dagens inlägg kommer du att lära dig skillnaden mellan primtal och sammansatta tal. Dessutom kommer vi att visa dig flera exempel för att hjälpa dig att förstå dem bättre.
Index
Vad är primtal?
Primtal är de tal som bara är delbara med sig själva och 1. Med andra ord, om vi försöker dela dem med ett annat tal blir resultatet inte ett helt tal. Så om vi delar talet med något annat än ett eller sig själv får vi en rest som inte är noll.
Primtal fram till 100
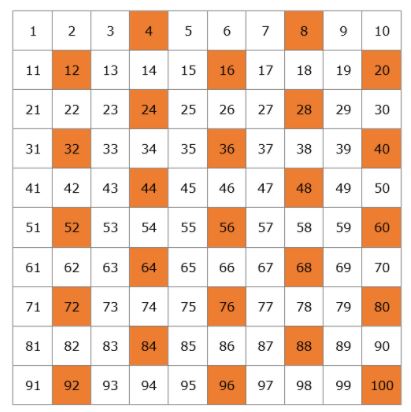
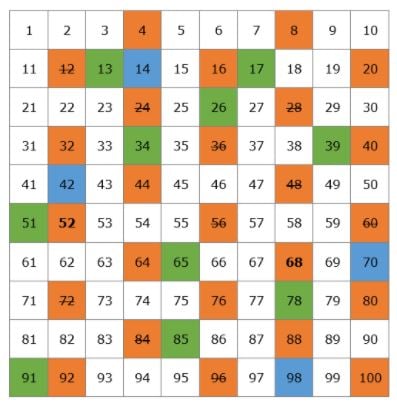
Vi ska skapa en tabell med alla primtal som finns fram till 100.
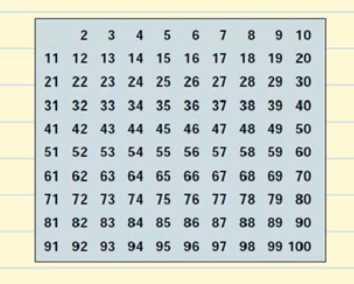

Låt oss börja med 2. 2 är ett primtal men alla multiplar av 2 kommer att vara sammansatta tal eftersom de kommer att vara delbara med 2. Vi stryker alla multiplar av 2 i tabellen.
Nästa primtal är 3, så vi kan stryka alla multiplar av 3 eftersom de kommer att vara sammansatta tal.
Efter 3 är nästa primtal 5, så vi stryker alla multiplar av 5.
Därefter har vi primtalet 7 och vi stryker alla multiplar av 7.
Nästa primtal är 11, så vi stryker alla multiplar av 11 som är 22, 33, 44, 55, 66, 77, 88 och 99. Alla dessa tal hade redan strukits ut, så vi är klara med att stryka ut alla sammansatta tal på vår tabell.

Detta är vår lista över primtal från 1 till 100. Du behöver inte lära dig dem utantill, men det vore bäst om du kom ihåg de mindre talen, till exempel 2, 3, 5, 7, 11, 13.
Hur många primtal finns det?
Den grekiske matematikern Eratosthenes (300-talet f.Kr.) utformade ett snabbt sätt att hitta alla primtal upp till ett givet tal. Det är en process som kallas Eratosthenes sil.
Märk att det mellan 1 och 100 finns 25 primtal. Hur många primtal finns det totalt sett? Vi har vetat sedan urminnes tider att det finns oändligt många, så det är omöjligt att räkna upp alla. Eftersom Euklid, som var den förste som visade att det fanns ett oändligt antal på 400-talet f.Kr., inte kände till begreppet oändlighet, sade han att ”primtalen är fler än någon fast mängd av dem”, vilket innebär att om du tänker dig 100 finns det fler, och om du tänker dig en miljon finns det ännu fler.
Primtal 100 till 1 000
Låt oss ta en titt på primtalen från 100 till 1 000.

Vi är ledsna att vi inte kan visa alla, eftersom du vet att det finns oändligt många. 😉
Primtalsexempel
För att hjälpa dig att bättre förstå primtal ska vi förklara en övning.
Sara har 6 godisbitar som hon vill dela med sig av, men hon vet inte hur många personer hon kan dela dem med så att alla får samma mängd och ingen blir över. Hur många sätt kan hon göra detta på?
Här är Sara och hennes 6 godisbitar:

Hur kan vi dela upp dem?
Det första och enklaste sättet är att ge dem till en person, med andra ord dela med 1. På så sätt kommer den personen att få 6 godisbitar.
Nästa möjlighet är att dela upp dem mellan 2 personer. Eftersom 6 dividerat med 2 är 3 får varje person 3 godisbitar!

Vi fortsätter med nästa siffra, 3. Om vi delar 6 godisbitar mellan 3 personer är det också en exakt delning och varje person får 2 godisbitar:

Vi fortsätter med siffrorna. Vi har inte exakta divisioner med 4 och 5, men det har vi med 6.
Då 6 dividerat med 6 är 1 kan vi ge 6 barn 1 godisbit vardera.

Vi ska samla in lite information. Vi har 6 godisbitar som vi kan dela (med en exakt delning) mellan 1, 2, 3 och 6 personer. Med andra ord kan vi dela talet 6 och få 0 som rest när vi delar det med 1, 2, 3 och 6. Dessa tal kallas divisorer av 6.
Vi ska försöka med ett annat tal, 7 till exempel.
Nu har Sara 7 godisbitar och vill dela med sig av dem, men vet inte hur många personer hon kan dela med sig av dem så att alla får samma mängd och ingen blir över. På hur många sätt kan hon göra detta?

Henry är så lycklig! Han fick alla godisbitar!
Är det andra sätt att göra det på? Vi kan inte dela 7 med 2, 3, 4, 5 eller 6, … men 7 är möjligt!
Sara kan dela godisbitarna mellan sju personer och ge dem en bit vardera:

Så 7 kan bara delas med 1 och 7, dess enda delare är 1 och 7. Detta är den typ av tal som vi kallar primtal.
Är det fler primtal? Självklart! Låt oss leta efter några fler:
- Är 4? Nej! Eftersom dess delare är 1, 2 och 4.
- Är 5? Ja! Eftersom dess divisorer är 1 och 5.
- Är 8? Nej! Eftersom dess delare är 1, 2, 4 och 8.
Kort sagt, ett tal är primtal om det bara har två delare: 1 och sig själv.
Nu kan du söka efter massor av primtal!
Hur man hittar primtal
Var noga uppmärksam! Vi ska ge dig ett knep för att veta om ett tal är primtal eller inte, utan att behöva leta efter dess divisorer, men på ett roligare sätt som ger oss divisorerna (om de har dem).
Låt oss välja ett slumpmässigt tal, 16 till exempel.
För att kontrollera om det är ett primtal eller inte ska vi använda en tabell som påminner mycket om Montessorikorten för multiplikation. Och vi kommer att få lika många bollar som antalet vi har valt. I det här fallet 16 bollar.
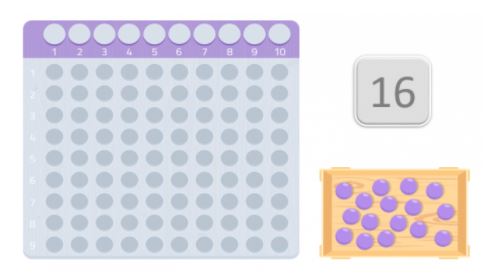
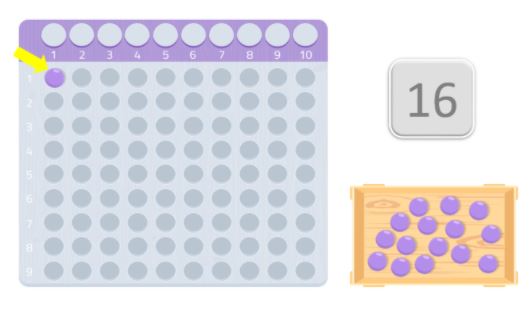
När vi har bordet och bollarna ska vi placera dem på bordet och börja med det första utrymmet och försöka bilda en rektangel. De tal som utgör rektangelns kanter är det talets divisorer.
Om vi bara lyckas bilda en rektangel med samma tal som vi använder och talet 1 blir det ett primtal.
Till exempel placerar vi i det här fallet 8 bollar i den första raden och ytterligare 8 i den andra. Som du kan se har vi bildat en rektangel och vi kan se att 8, liksom 2, är delare av talet 16. Därför är 16 inte ett primtal eftersom, som ni vet, primtal är de som bara är delbara med sig själva och 1.
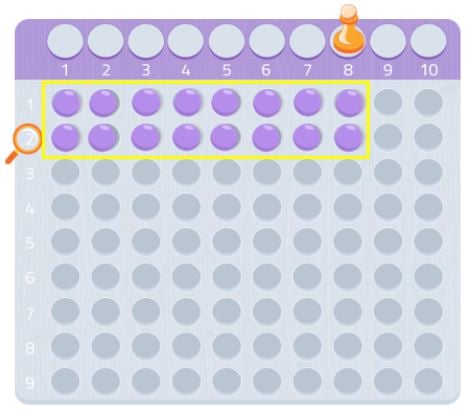
Vi kan försöka med ett annat tal, 7 till exempel.
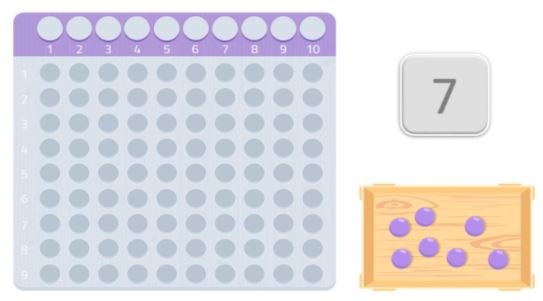
Som vi kan se kan vi inte göra en hel rektangel, vi skulle sakna en kula. Eftersom vi inte kan bilda en rektangel kan vi säga att talet 7 inte har några andra delare förutom sig självt och 1, vilket vi kan se i följande bild:
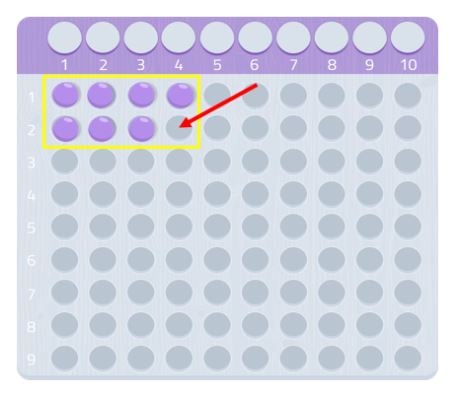
Därför är 7 ett primtal!
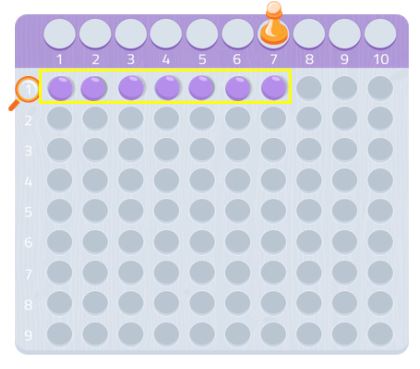
Prova med vilket annat tal som helst, du kommer att se hur det fungerar! Du kan använda grafenpapper och leta efter rektanglar som använder det antalet rutor.
Varför är primtal viktiga?
Primtal är nyckeln till aritmetik, nedan ser du ett exempel som visar hur viktiga de är, inte bara inom matematiken utan även i naturen.
Vad menar vi när vi säger att primtal är nyckeln till aritmetik?
Det beror på att varje tal består av en unik produkt som består av en serie av dessa tal.
Man tror att de har studerats i cirka 20 000 år då en av våra förfäder skrev ner en serie primtal (11, 13, 17 och 19) på Ishango-benet. Som om detta vore en tillfällighet har det bekräftats att de gamla egyptierna arbetade med dem för 4 000 år sedan.
Det är dessutom så att naturen känner till dem mycket väl och vissa arter har kunnat upptäcka dem under hela sin utveckling och dra nytta av dem för sin överlevnad.
Jag syftar på flera arter av cikador, till exempel Magicicada septendecium som lever i Nordamerika. Denna cikadaart har etablerat sin fortplantningscykel runt 13 eller 17 år, inte 12, 14, 15, 16 eller 18 – exakt 13 eller 17. Detta gör det möjligt för dem att undvika rovdjur som också har periodiska reproduktionscykler; tänk dig ett rovdjur med en 4-årig reproduktionscykel.
Om en cikadas livscykel var 12 eller 14 år skulle den sammanfalla med ett rovdjur mycket ofta, mycket oftare än om den var 13 eller 17 år. Exakt 2 gånger vart 100:e år, medan de annars skulle sammanfalla i 11 cykler vilket skulle äventyra artens utveckling.
Säkerheten i den elektroniska kommunikationen bygger också på primtal. Varje krypterat meddelande som skickas över internet (meddelandenätverk, inköp eller elektroniska bankärenden) har ett stort tal kopplat till sig, och det är mycket svårt att veta var det är primtal eller inte. Mottagaren har en av dess divisorer, och det är därför de kan dekryptera det. Att ha primtal är alltså avgörande för vår integritet när vi kommunicerar elektroniskt.
Vad är sammansatta tal?
Komposita tal är de tal som är delbara med 1 och sig själva samt andra tal.
Vi ska titta på ett exempel på ett primtal och ett komposittal.
11 kan skrivas som multiplikationen 1 x 11, men det kan inte skrivas som någon annan multiplikation av naturliga tal. Det har bara delarna 1 och 11 och är därför ett primtal.
12 kan skrivas som multiplikationen 1 x 12 och som multiplikationerna 3 x 4 och 2 x 6. Eftersom 12 är delbart med fler tal än 1 och sig självt är 12 ett sammansatt tal.
Är 1 ett primtal?
Det finns människor som tror det eftersom de säger att 1 bara kan delas med 1 och sig självt, men inom matematiken har talet 1 förkastats som ett primtal eftersom det bara har en divisor. Faktum är att kriteriet ”ett positivt heltal är primtal om det har exakt två positiva divisorer” används för att utesluta talet 1 från listan över primtal. Det beror inte på att vi är petiga, men om talet ett ansågs vara primtal skulle många matematiska egenskaper behöva sägas annorlunda.
Så, 1 är ett sammansatt tal?
Nja, det är inte heller sammansatt eftersom det inte kan sättas som en produkt av primtal. Talet 1 är varken primtal eller sammansatt. Och innan du frågar, noll är inte heller primtal eller sammansatt, men det beror på att alla de överväganden vi förklarade för positiva tal, det vill säga större än noll.
Delare av ett tal
Divaren av ett tal är det värde som delar talet i exakta delar, med andra ord, har en rest på 0.
Som exempel ska vi beräkna divisorerna för 24.
Vi börjar dividera med de minsta talen och börjar med 1.
Nästa tal är 6, men eftersom vi redan vet att 6 är en divisor till 24 har vi räknat ut divisorerna till 24.
Video: Faktorisering och primtal
Om du vill veta mer om primtal och sammansatta tal kan du ta en titt på följande video. Du kommer också att lära dig begreppet faktorisering med hjälp av Montessoritabellen.
Den här videon är en av våra interaktiva handledningar och även om den inte är interaktiv kan du ändå titta på den så många gånger du vill och dela den med dina vänner. Om du vill få tillgång till våra interaktiva handledningar ska du registrera dig hos Smartick! Onlinemetoden som hjälper barn mellan 4 och 14 år att lära sig och öva matematik.
Om du vill fortsätta lära dig om primtal och den bästa matematiken anpassad till din nivå, registrera dig med Smartick och prova gratis!
Lär dig mer:
- Primtal och sammansatta tal
- Primtal: Ett knep som hjälper dig att identifiera dem
- Primtal: Hur man hittar dem med Eratosthenes sil
- Lär dig att faktorisera primtal
- Primtal Aktiviteter med Smartick



- Författare
- Renoverade inlägg
Ett tvärvetenskapligt och mångkulturellt team bestående av matematiker, lärare, professorer och andra utbildningsexperter!
De strävar efter att skapa det bästa möjliga matematiska innehållet.
- Exempel på matematiska ordproblem i 3:e klass med lösningar – 03/25/2021
- Konsekventa inre vinklar: Vad de är och hur man hittar dem med exempel – 03/11/2021
- Exempel på ordproblem i andra klass med lösningar – 02/04/2021