Co je to frekvence? Frekvence je „jak často“ se něco děje. Protože zvuk je kmitání, používáme frekvenci k popisu toho, jak často něco kmitá. frekvence se měří v hertzích (Hz), což je jednoduše „jak často za sekundu“, takže něco, co kmitá rychlostí 1 Hz, kmitá jednou za sekundu. „Úplná“ vibrace se nazývá „cyklus“ a měří se při jednom úplném vrcholu a korytu vlny (tj. maximální vzdálenost nebo „amplituda“ nad středem nebo bodem „0“, který je znázorněn na ose x). (V počátcích elektronické hudby se místo Hz používal termín „cykly za sekundu“, který dnes můžete vidět na mnoha starých/vintage syntezátorech).
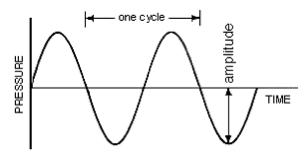
Výše uvedený obrázek je sinusoida – nejčistší reprezentace jedné frekvence nebo vibrace. Doba, za kterou vlna dokončí jeden cyklus, je frekvence vlny (opět „jak často“ vibruje). Více kmitů za sekundu (tj. rychlejší kmitání) vytváří „vyšší“ zvukové frekvence a méně kmitů za sekundu (tj. pomalejší kmitání) vytváří „nižší“ zvukové frekvence. Člověk slyší pouze frekvence zhruba v rozmezí 20 Hz – 20 000 Hz (20 kHz) (více viz https://en.wikipedia.org/wiki/Hearing_range).
V hudbě spolu souvisí pojmy frekvence, výška a tón.Tón je zvuk s jednou nebo více identifikovatelnými frekvencemi. Frekvence jeempirické měření fyzikálního jevu, definované jako počet cyklů(kmitů) za sekundu. Výška tónu je subjektivní vnímání relativní výšky tónu, jako je „vysoký“ nebo „nízký“ (více o tom viz Konceptuální modely a mezidoménové mapování Lawerence Zbikowskéhohttp://zbikowski.uchicago.edu/pdfs/ZbikowskiConceptualmodels_1997.pdf).
Zatímco frekvence jsou reprezentovány čísly (Hz), výška tónu je reprezentována písmeny. Pokud jste například někdy slyšeli „ladit“ orchestr nazačátku koncertu, jeden hráč (obvykle hoboj nebo housle) hraje „A“ o frekvenci 440 Hz (označované jako A440). U výšky tónu používáme pouze písmena A, B, C, D, E, F a G (další symboly se používají pro jejich zvýšení nebo snížení, o tom později). Tyto výšky se opakují každých 8 tónů, kterým se říká oktáva.Abychom rozlišili, o které oktávy se jedná, když mluvíme o výšce tónu, přidává se za písmeno číslo. Například A440 (Hz) se z hlediska výšky tónu nazývá A4. Nenechte se však zmást, číslice 4 označuje oktávu, ve které máme na mysli dané A (konkrétně u klavíru) – je to jen náhoda, že frekvence je 440, číslice 4 se na ni konkrétně nevztahuje. Možná se ptáte, proč je tedy A4 440 Hz… na tuto otázku je poměrně složitá odpověď, ale nakonec je skutečně libovolná. Jednoduše řečeno, v 19. století se sešla parta lidí a rozhodla, že tomu tak je. (Pokud se chcete o tomto tématu dozvědět více, najděte si něco o A440 nebo o standardech výšky tónu/laděníhttps://en.wikipedia.org/wiki/A440(pitchstandard)).
Je důležité si uvědomit, že frekvence je absolutní, zatímco výška tónu je relativní (tyto relativní změny se označují jako „ladění“). Výšky tónů používáme k popisu jejich vztahu (tj. poměru) k jiným výškám tónů a analýza těchto vztahů je základem „hudební teorie“. Obecně jsme se shodli, že A4 je definována jako tón, jehož frekvence je 440 Hz (absolutní referenční hodnota). Pomocí určitého vzorce ladění pak můžeme určit „výšku“ nebo „ladění“ všech ostatních tónů ve vztahu k tomuto tónu.
Jedním z velmi důležitých aspektů celé hudební teorie je, že oktávy jsou specificky definovány jako „zdvojnásobení“ nebo „rozpůlení“ frekvence tónu. Například frekvence 220 Hz, 440 Hz a 880 Hz jsou všechny A, ale existují v různých oktávách: A3, A4 a A5. V západní hudební teorii jsme se obecně (a upřímně řečeno svévolně) shodli na tom, že v každé oktávě existuje 12 stejných dílčích tónů nebo výšek. Jak tedy určíme, kde jsou tyto další tóny „naladěny“ ve vztahu k této A440? No, po mnoha letech experimentů bylo rozhodnuto, že následující vzorec určuje relativní vztah mezi výškami tónů (přesněji řečeno frekvenci f n-té klávesy na standardním klavíru):
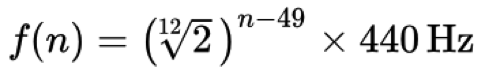https://en.wikipedia.org/wiki/Pianokeyfrequencies
Zjednodušeně řečeno, každý tón/výška tónu v ladění západní klasické hudby je odvozen tak, že začneme s A440 jako „referenčním tónem“ a pak jej vynásobíme nebo vydělíme dvanáctou odmocninou ze dvou (~1,059463), abychom získali další tón nad nebo pod tímto referenčním tónem. Číslo 49 je v tomto případě libovolné (A4 je 49. klávesa na standardní klaviatuře klavíru) a v počítačové hudbě obvykle používáme pro výpočty čísla MIDI – například A440 je MIDI klávesa číslo 69 (více o MIDI standardech v samostatné lekci).
Je třeba poznamenat, že tento vzorec představuje pouze jeden konkrétní styl „ladění“, který existuje v rámci západní tradice klasické hudby a je obecně používán jako „světový standard“, když mluvíme obecně o vztazích mezi výškou tónu a frekvencí, přestože tyto vztahy jsou libovolné a v různých kulturách a tradicích existují i jiné systémy ladění.Tento systém zachovává důležité „pravidlo“, že oktávy jsou definovány jako přesné zdvojení nebo zdvojení frekvencí při zachování stejných poměrů (výšky tónu) dělení každé oktávy na 12 stejných částí. Tento systém ladění nazýváme 12tónový ekvalent a slouží jako základ pro většinu světa jako základní a dohodnutý systém ladění, zejména pokud jde o standardizaci elektronických hudebních zařízení. (Všechny klavíry jsou naladěny v tomto systému a všechnaMIDI data se řídí tímto obecným principem).
V hudební terminologii popisujeme výšky tónů (nebo tóny) jako vzestupné nebo sestupné ve smyslu „kroků“. Existují dva druhy kroků:půlkroky a celé kroky (nazývané také půltóny nebo celé tóny). zvýšení tónů o jeden půlkrok (tj. půltón) se označuje symbolem ♯ zvaným „sharp“ (číslice nebo hashtag symbol) a snížení tónů o půl kroku se označuje symbolem ♭ zvaným „flat“ (často se také používá malé písmeno „b“). Půltóny nebo půlkroky si můžete představit jako minimální vzdálenost mezi dvěma sousedními klávesami klavíru nebo kytarovými pražci.
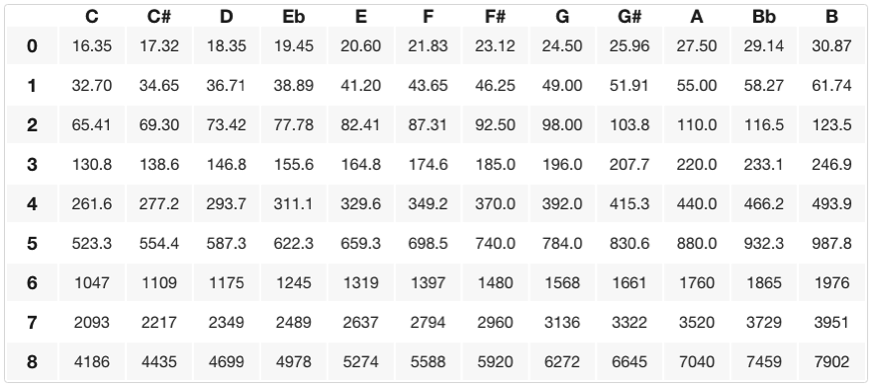
Pro získání frekvence o půltón vyšší než A4 vynásobíme 440 Hz dvanáctou odmocninou ze dvou a získáme ~466,2 Hz, což nám dává A# (nebo Bb). A# a Bb se nazývají „enharmonické tóny“ neboli tóny, které mají technicky stejnou frekvenci, ale mohou se „psát“ jinak v závislosti na „tónině“ nebo hudebním kontextu, o kterém konkrétně mluvíme (více o tom v samostatné lekci). Abychom získali frekvenci o celý stupeň vyšší než A4, můžeme 440 Hz dvakrát vynásobit dvanáctou odmocninou ze dvou, čímž získáme ~493,9 Hz neboli B4. Níže je tabulka všech konkrétních frekvencí s jejich vztahem k výšce tónu/oktávě (názvy not jsou na ose x a čísla oktáv na ose y).
https://www.seventhstring.com/resources/notefrequencies.html
Tento soubor „dvanácti not na oktávu“ se nazývá chromatická stupnice. „Stupnice“ je soubor not ve vzestupném/klesajícím pořadí začínající/končící na základní frekvenci nebo výšce tónu. Chromatická stupnice začíná na libovolné výšce tónu a stoupá (nebo klesá) o 11 následně sousedících půlstupňů (půltónů) od jejího základu. Na výše uvedeném grafu můžete najít konkrétní frekvence nebo tóny/výšky jakékoli chromatické stupnice tak, že začnete na daném tónu (základním) a budete počítat nahoru nebo dolů o 11 půltónů (sousedních výšek).
Pokud jste si všimli, některé tóny ve výše uvedeném grafu jsou „napsány“ s # (sharp), zatímco jiné jsou napsány s b (flat). Teoreticky lze jakoukoli notu zvýšit nebo snížit o půl nebo celý krok/tón přidáním jednoho z těchto symbolů za ni. Vzhledem k rozšířenosti a předvídatelnosti západní hudebně-teoretické praxe však existují konvence, podle nichž se určité noty „píší“ určitým způsobem. Pokud jde o „enharmonické hláskování“ not a výšek tónů (noty, které mají stejnou frekvenci, ale jsou reprezentovány jako různé výšky tónů), výše uvedená tabulka představuje nejběžnější hláskování not a výšek tónů s ohledem na tradiční praxi „tónových značek“ v hudbě, ale nezahrnuje všechny možnosti. Následující noty jsou běžné enharmonické hlásky (lomítka označují noty/výšky, které mají stejnou frekvenci, ale mohou být reprezentovány nebo „hláskovány“ jako různé výšky tónů):
C#/Db D#/Eb F#/Gb G#/Ab A#/Bb
Teoreticky lze samozřejmě jakoukoli notu zvýšit nebo snížit o půl stupně (půltón) nebo dokonce o celý stupeň (celý tón) pomocí symbolu # nebo b a pokročilejší hudební teorie se zabývá takzvanými dvojhmaty a -harfy.Aniž bychom se tím příliš zabývali, všechny stupnice nebo hudební tóniny jsou souborem půlstupňů a celých stupňů a hláskování těchto tónů napovídá interpretovi o vztazích (tj. poměrech) mezi tóny, které skladatel používá.
- Hertz (Hz)
- frekvence
- tón
- výška
- A4 (A440)
- oktávy
- celé kroky (celé tóny)
- poloviční kroky (půltóny)
Samostatně-Kvíz
- Výška tónu G3 má základní frekvenci 196 Hz. Bez nahlížení do tabulky,jaké jsou frekvence tónů G2 a G4 (o oktávu níže a výše než G4)?
Další zdroje
- Vlastnosti zvuku – Khan Academy
- Zvuk: Crash Course Physics