Prozkoumejme, co se stane, když se pod symbolem radikálu (jako radicand) objeví záporné hodnoty pro odmocniny krychlové a odmocniny.
V některých situacích jsou záporná čísla pod symbolem radikálu v pořádku. Například 
není problém, protože (-2) – (-2) – (-2) = -8, takže odpověď je -2. V úlohách na krychlové kořeny je možné zápornou hodnotu třikrát vynásobit sebou samým a získat zápornou odpověď.
Problémy však nastanou, když se podíváme na úlohu jako 
. Tato úloha o odmocninách se ptá na číslo vynásobené sebou samým, které dá součin (odpověď) rovný -16. Jednoduše neexistuje způsob, jak vynásobit číslo samo sebou a získat záporný výsledek. Uvažujme: (4) – (4) = 16 a (-4) – (-4) = 16.
|
KUBOVÉ KOŘENY:
 |
ALE
|
KVALITNÍ KOŘENY:
 |
|
Ano, (-2) x (-2) x (-2) = -8. To znamená, že (-2) x (-2) x (-2) = -8.
Není problém. |
Ne! (4) x (4) ≠ -16. |
Viníky jsou odmocniny! Potíže nastávají, když se setkáte se zápornou hodnotou pod odmocninou. Není možné odmocnit hodnotu (vynásobit ji sebou samou) a dojít k záporné hodnotě. Co tedy uděláme?
 |
Odmocnina ze záporného čísla mezi množinou reálných čísel neexistuje
|
Když se problémy se záporným číslem pod odmocninou objevily poprvé, domnívali se matematici, že řešení neexistuje. Viděli rovnice jako x2 + 1 = 0 a přemýšleli, co vlastně řešení 
znamená.
Ve snaze vyřešit tento problém matematici „vytvořili“ nové číslo i, které bylo označováno jako „imaginární číslo“, protože nebylo v množině „reálných čísel“. Na toto nové číslo se pohlíželo s velkou skepsí. Imaginární číslo se poprvé objevilo v tisku v roce 1545.
 |
Imaginární číslo „i“ je odmocnina ze záporné jedničky. |
Imaginární číslo má jedinečnou vlastnost, že při odmocnění je výsledek záporný.
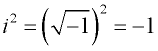
Přemýšlejte: 
Proces zjednodušování radikálu obsahujícího záporný činitel je stejný jako normální zjednodušování radikálu. Jediný rozdíl je v tom, že 
bude nahrazen znakem „i „.
Při dalším výzkumu imaginárních čísel se zjistilo, že vlastně vyplňují mezeru v matematice a slouží užitečnému účelu. Imaginární čísla jsou nezbytná pro studium věd, jako je elektřina, kvantová mechanika, analýza vibrací a kartografie.
Když se imaginární i spojilo s množinou reálných čísel, vznikla všezahrnující množina komplexních čísel.
.
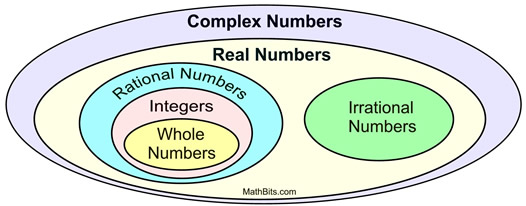