Investiguemos qué ocurre cuando aparecen valores negativos bajo el símbolo radical (como radicando) para raíces cúbicas y raíces cuadradas.
En algunas situaciones, los números negativos bajo un símbolo radical están bien. Por ejemplo, 
no es un problema ya que (-2) – (-2) – (-2) = -8, lo que hace que la respuesta sea -2. En los problemas de raíces cúbicas, es posible multiplicar un valor negativo por sí mismo tres veces y obtener una respuesta negativa.
Las dificultades, sin embargo, surgen cuando observamos un problema como 
. Este problema de raíz cuadrada pide un número multiplicado por sí mismo que dará un producto (respuesta) de -16. Simplemente no hay manera de multiplicar un número por sí mismo y obtener un resultado negativo. Considera: (4) – (4) = 16 y (-4) – (-4) = 16.
|
RAÍCES DEL CUBO:
 |
PERO
|
RAÍCES CUADRADAS:
 |
|
Sí, (-2) x (-2) x (-2) = -8.
No hay problema. |
¡No! (4) x (4) ≠ -16. |
¡Las raíces cuadradas son las culpables! Las dificultades surgen cuando se encuentra un valor negativo bajo una raíz cuadrada. No es posible elevar al cuadrado un valor (multiplicarlo por sí mismo) y llegar a un valor negativo. Entonces, ¿qué hacemos?
 |
La raíz cuadrada de un número negativo no existe entre el conjunto de los Números Reales.
|
Cuando aparecieron por primera vez los problemas con negativos bajo una raíz cuadrada, los matemáticos pensaron que no existía una solución. Veían ecuaciones como x2 + 1 = 0, y se preguntaban qué significaba realmente la solución 
.
En un esfuerzo por abordar este problema, los matemáticos «crearon» un nuevo número, i, al que se denominó «número imaginario», ya que no estaba en el conjunto de los «Números Reales». Este nuevo número fue visto con mucho escepticismo. El número imaginario apareció por primera vez impreso en el año 1545.
 |
El número imaginario «i» es la raíz cuadrada de uno negativo. |
Un número imaginario posee la propiedad única de que cuando se eleva al cuadrado, el resultado es negativo.
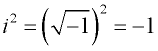
Considera: 
El proceso de simplificación de un radical que contiene un factor negativo es el mismo que la simplificación normal de radicales. La única diferencia es que el 
será sustituido por una «i «.
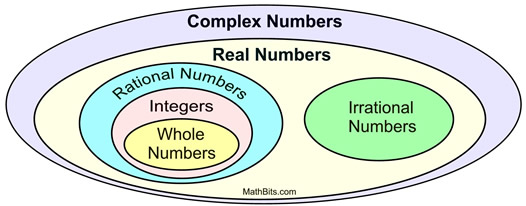
Al continuar la investigación con los números imaginarios, se descubrió que en realidad llenaban un vacío en las matemáticas y tenían un propósito útil. Los números imaginarios son esenciales para el estudio de ciencias como la electricidad, la mecánica cuántica, el análisis de vibraciones y la cartografía.
Cuando la i imaginaria se combinó con el conjunto de los Números Reales, se formó el conjunto de los Números Complejos.
