Låt oss undersöka vad som händer när negativa värden visas under radikalsymbolen (som radikand) för kubikrötter och kvadratrötter.
I vissa situationer är det okej med negativa tal under en radikal symbol. Till exempel är 
inget problem eftersom (-2) – (-2) – (-2) – (-2) = -8, vilket gör att svaret blir -2. I kubikrotsproblem är det möjligt att multiplicera ett negativt värde med sig självt tre gånger och få ett negativt svar.
Svårigheter utvecklas dock när vi tittar på ett problem som 
. Detta kvadratrotsproblem frågar efter ett tal multiplicerat med sig självt som ger en produkt (svar) på -16. Det finns helt enkelt inget sätt att multiplicera ett tal med sig självt och få ett negativt resultat. Tänk på följande: (4) – (4) = 16 och (-4) – (-4) = 16.
|
CUBE ROOTS:
 |
BUT
|
KVADRÄTTSRÖTTER:
 |
|
Ja, (-2) x (-2) x (-2) x (-2) = -8.
Inga problem. |
Nej! (4) x (4) ≠ -16. |
Kvadratrötter är bovarna! Svårigheterna uppstår när man stöter på ett negativt värde under en kvadratrot. Det är inte möjligt att kvadrera ett värde (multiplicera det med sig självt) och komma fram till ett negativt värde. Vad gör vi då?
 |
Kvadratroten av ett negativt tal existerar inte bland uppsättningen reella tal.
|
När problem med negativa värden under en kvadratrot först dök upp trodde matematikerna att en lösning inte fanns. De såg ekvationer som x2 + 1 = 0 och undrade vad lösningen 
egentligen betydde.
I ett försök att lösa detta problem ”skapade” matematikerna ett nytt tal, i, som kallades ett ”imaginärt tal”, eftersom det inte ingick i mängden ”reella tal”. Detta nya tal betraktades med stor skepsis. Det imaginära talet dök först upp i tryck år 1545.
 |
Det imaginära talet ”i” är kvadratroten av negativt ett. |
Ett imaginärt tal har den unika egenskapen att när det kvadreras är resultatet negativt.
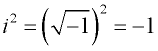
Konsumerera: 
Processen att förenkla en radikal som innehåller en negativ faktor är densamma som normal radikalförenkling. Den enda skillnaden är att 
ersätts med ett ”i ”.
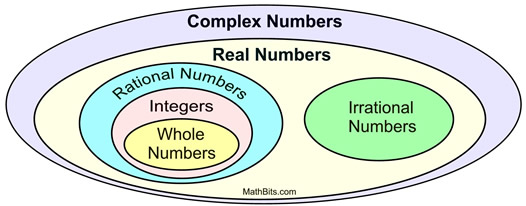
När forskningen om imaginära tal fortsatte upptäcktes det att de faktiskt fyllde en lucka i matematiken och tjänade ett användbart syfte. De imaginära talen är viktiga för studiet av vetenskaper som elektricitet, kvantmekanik, vibrationsanalys och kartografi.
När det imaginära i:et kombinerades med uppsättningen reella tal bildades den allomfattande uppsättningen komplexa tal.
