Vamos investigar o que acontece quando valores negativos aparecem sob o símbolo radical (como o radicand) para raízes cúbicas e raízes quadradas.
Em algumas situações, os números negativos sob um símbolo radical são OK. Por exemplo, 
não é um problema pois (-2) – (-2) – (-2) – (-2) = -8, fazendo com que a resposta -2. Em problemas de raiz cúbica, é possível multiplicar um valor negativo vezes três vezes e obter uma resposta negativa.
Dificuldades, no entanto, desenvolvem-se quando olhamos para um problema como 
. Este problema de raiz quadrada é pedir um número multiplicado vezes que dará um produto (resposta) de -16. Simplesmente não há maneira de multiplicar um número multiplicado e obter um resultado negativo. Considere: (4) – (4) = 16 e (-4) – (-4) = 16.
|
CUBE ROOTS:
 |
>
MAS
|
SQUARE ROOTS:
 |
|
Sim, (-2) x (-2) x (-2) = -8.
Sem problema. |
Nope! (4) x (4) ≠ -16. |
Raízes quadradas são os culpados! As dificuldades surgem quando você encontra um valor negativo sob uma raiz quadrada. Não é possível ajustar um valor (multiplicá-lo vezes) e chegar a um valor negativo. Então, o que é que fazemos?
 |
A raiz quadrada de um número negativo não existe entre o conjunto de Números Reais.
|
Quando problemas com negativos sob uma raiz quadrada apareceram pela primeira vez, os matemáticos pensaram que não existia uma solução. Eles viram equações como x2 + 1 = 0, e se perguntaram o que a solução 
realmente significava.
Num esforço para resolver este problema, os matemáticos “criaram” um novo número, i, que foi referido como um “número imaginário”, já que não estava no conjunto de “Números Reais”. Este novo número foi visto com muito cepticismo. O número imaginário apareceu pela primeira vez na impressão no ano 1545.
 |
O número imaginário “i” é a raiz quadrada de um negativo. |
Um número imaginário possui a propriedade única que quando quadrado, o resultado é negativo.
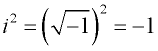
Considerar: 
O processo de simplificação de um radical contendo um fator negativo é o mesmo que a simplificação radical normal. A única diferença é que o 
será substituído por um “i”.
Como a pesquisa com números imaginários continuou, descobriu-se que eles realmente preencheram uma lacuna em matemática e serviram a um propósito útil. Os números imaginários são essenciais para o estudo de ciências como eletricidade, mecânica quântica, análise de vibração e cartografia.
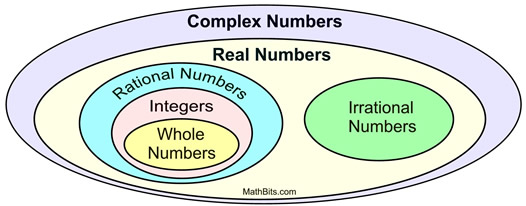
Quando o i imaginário foi combinado com o conjunto de Números Reais, o conjunto abrangente de Números Complexos foi formado.
