Hvad er frekvens? Frekvens er “hvor ofte” noget sker. Da lyd ervibrationer, bruger vi frekvens til at beskrive, hvor ofte noget vibrerer.Frekvensen måles i hertz (Hz), som simpelthen er “hvor ofte pr. sekund”.Så noget, der svinger med 1 Hz, vibrerer en gang i sekundet. En “komplet” vibration kaldes en “cyklus” og måles ved en bølges fulde top og lavpunkt (dvs. den maksimale afstand eller “amplitude” over det midterste punkt eller “0”-punktet, som er repræsenteret på x-aksen). (I den elektroniske musiks tidlige dage brugte man udtrykket “cyklusser pr. sekund” i stedet for Hz, som man i dag kan se på mange gamle/ældre synthesizere).
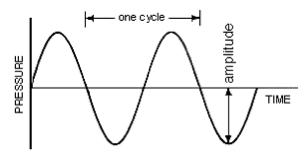
Overstående billede er en sinusbølge – den reneste repræsentation af en enkelt frekvens eller vibration. Den tid, det tager bølgen at gennemføre en cyklus, er bølgens frekvens (igen, “hvor ofte” den vibrerer). Flere vibrationer pr. sekund (dvs. hurtigere svingninger) giver “højere” klingende frekvenser, og færre vibrationer pr. sekund (dvs. langsommere svingninger) giver “lavere” klingende frekvenser. Mennesker kan kun høre frekvenser på omkring 20 Hz – 20.000 Hz (20 kHz) (se mere herom i https://en.wikipedia.org/wiki/Hearing_range).
I musikken er begreberne frekvens, tonehøjde og tone beslægtede.En tone er en lyd med en eller flere identificerbare frekvenser. Frekvens erden empiriske måling af et fysisk fænomen, defineret som antal cyklusser(af vibrationer) pr. sekund. Tonehøjde er en subjektiv opfattelse af den relative højde af en tone, som i “høj” eller “lav” (for mere om dette se Conceptual Modelsand Cross-Domain Mapping af Lawerence Zbikowskihttp://zbikowski.uchicago.edu/pdfs/ZbikowskiConceptualmodels_1997.pdf).
Mens frekvenser repræsenteres med tal (Hz), repræsenteres tonehøjde med bogstaver. Hvis du f.eks. nogensinde har hørt et orkester “stemme” i begyndelsen af en koncert, spiller en enkelt spiller (normalt en obo eller violin) et “A” målt ved 440 Hz (benævnt A440). Med tonehøjde bruger vi kun bogstaverne A, B, C, D, E, F og G (der bruges yderligere symboler til at hæve eller sænke dem, mere om dette senere). Disse tonehøjder gentages hver 8. tone, hvilket kaldes en oktav.For at kunne skelne mellem, hvilke oktaver vi henviser til, når vi taler om tonehøjde, tilføjes der et tal efter bogstavet. F.eks. kaldes A440 (Hz) for A4, når det drejer sig om tonehøjde. Lad dig dog ikke forvirre her, 4 henviser til den oktav, som vi henviser til det pågældende A (specifikt på klaveret) – det er bare et tilfælde, at frekvensen tilfældigvis er 440, 4 henviser ikke specifikt til det. Men hvorfor er A4 så 440 Hz, spørger du måske….ja, der er et ret kompliceret svar på det spørgsmål, men i sidste ende er det faktisk arbitrært. Kort sagt, en flok mennesker fandt sammen i det 19. århundrede og besluttede, at det var tilfældet. (Hvis du gerne vil vide mere om emnet, så undersøg A440 eller pitch/tuning standardshttps://en.wikipedia.org/wiki/A440(pitchstandard)).
Det er vigtigt at bemærke, at frekvens er absolut, mens tonehøjde er relativ (disse relative ændringer betegnes som “tuning”). Vi bruger tonehøjder til at beskrive deres forhold (dvs. ratio) til andre tonehøjder, og analysen af disse forhold er grundlaget for “musikteori”. Generelt er vi blevet enige om, at A4 er defineret som den tonehøjde, hvis frekvens er 440 Hz (en absolut reference). Vi kan derefter bestemme “tonehøjden” eller “stemningen” af alle de andre toner i forhold til denne ved hjælp af en bestemt stemmingsformel.
Et meget vigtigt aspekt af al musikteori er, at oktaver specifikt defineres som “fordobling” eller “halvering” af en tonehøjdes frekvens. F.eks. er frekvenserne 220 Hz, 440 Hz og 880 Hz alle A’er, men de findes i forskellige oktaver: henholdsvis A3, A4 og A5. I vestlig musikteori er vi generelt (og ærlig talt arbitrært) enige om, at der inden for hver oktav er 12 lige store underopdelinger eller tonehøjder. Hvordan kan vi så afgøre, hvor disse andre toner er “stemt” i forhold til A440? Efter mange års eksperimentering blev det besluttet, at følgende formel bestemmer det relative forhold mellem tonehøjder (mere specifikt frekvensen f på den niende tangent på et standardklaver):
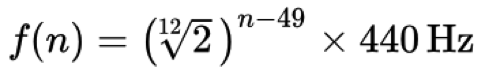https://en.wikipedia.org/wiki/Pianokeyfrequencies
Simpelt sagt er hver tone/ tonehøjde i den vestlige klassiske musiks stemning afledt ved at starte med A440 som en “referencetone” og derefter gange eller dividere med den tolvte rod af to (~1,059463) for at komme til en anden tone over eller under denne referencetone. Tallet 49 er i dette tilfælde arbitrært (A4 er den 49. tangent på et standard klaviatur), og i computermusik bruger vi typisk MIDI-numre til vores beregninger – A440 er f.eks. MIDI tangent nummer 69 (mere om MIDI-standarder i en separat lektion).
Det skal bemærkes, at denne formel kun repræsenterer en bestemt stil af “stemning”, der findes inden for den vestlige klassiske musiktradition, og som generelt bruges som “verdensstandard”, når man taler om tonehøjde/frekvens/tonerelationer generelt, selv om disse relationer er vilkårlige, og der findes andre stemmesystemer inden for forskellige kulturer og traditioner.Dette system bevarer en vigtig “regel”, nemlig at oktaver defineres som en nøjagtig fordobling eller halvering af frekvenser, samtidig med at de samme (tonehøjde-)forhold bevares ved at dele hver oktav op i 12 lige store dele. Vi kalder dette stemmesystem for 12-tone equaltemperament, og det tjener som grundlag for det meste af verden som et grundlæggende og vedtaget stemmesystem, især når det drejer sig om standardisering af elektronisk musikudstyr. (Alle klaverer er stemt i dette system, og alle MIDI-data følger dette generelle princip).
I musikterminologien beskriver vi tonehøjder (eller toner) som stigende eller faldende i form af “trin”. Der findes to slags trin: halve trin og hele trin (også kaldet halvtoner eller hele toner).At hæve toner med et halvt trin (dvs. en halv tone) angives med et ♯symbol kaldet et ‘sharp’ (tal- eller hashtag-symbol), og at sænke toner med et halvt trin angives med et ♭-symbol kaldet et ‘flat’ (et lille ‘b’ bruges også ofte). Du kan tænke på halvtoner eller halve trin som den mindste afstand mellem to tilstødende klavertangenter eller guitarbånd.
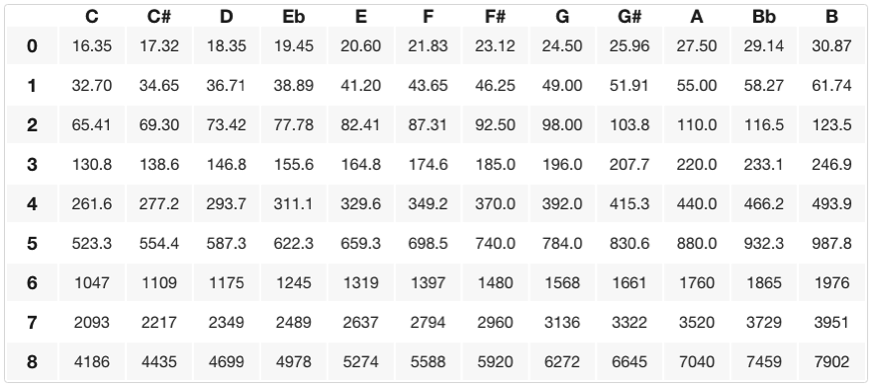
For at få frekvensen en halv tone op fra A4 skal vi gange 440 Hz med den tolvte rod af to, så vi får ~466,2 Hz, hvilket giver os et A# (eller Bb). A# og Bb kaldes “enharmoniske toner”, eller tonehøjder, der teknisk set har samme frekvens, men som kan “staves” forskelligt afhængigt af den “toneart” eller musikalske kontekst, vi specifikt taler om (mere om dette i en separat lektion). For at få frekvensen et helt trin op fra A4 kan vi gange 440 Hz to gange med den tolvte rod af to, hvilket giver os ~493,9 Hz eller B4. Nedenfor er en tabel over alle de specifikke frekvenser med deres tonehøjde/oktavemæssige forhold (nodenavne er på x-aksen og oktavtal på y-aksen).
https://www.seventhstring.com/resources/notefrequencies.html
Denne samling af “tolv toner pr. oktav” kaldes den kromatiske skala.En “skala” er en samling af toner i stigende/faldende rækkefølge, der begynder/slutter på en grundfrekvens eller tonehøjde. En kromatisk skala starter på en vilkårlig tonehøjde og stiger (eller falder) med 11 efterfølgende tilstødende halve trin (halvtoner) fra dens grundtone. På skemaet ovenfor kan du finde de specifikke frekvenser eller toner/toner i en kromatisk skala ved at starte på en given tone (grundtonen) og tælle 11 halvtoner op eller ned (tilstødende tonehøjder).
Hvis du har bemærket det, er nogle af tonerne i skemaet ovenfor “stavet” med et # (skarpt), mens andre er stavet med et b (flad). Teoretisk set kan enhver tone hæves eller sænkes et halvt eller helt trin/en hel tone ved at tilføje et af disse symboler efter den. Der er dog konventioner om, at visse toner “staves” på en bestemt måde på grund af udbredelsen og forudsigeligheden af den vestlige musikteoretiske praksis. Med hensyn til “enharmoniske stavemåder” af toner og tonehøjder (toner, der har samme frekvens, men er repræsenteret som forskellige tonehøjder) repræsenterer ovenstående tabel de mest almindelige stavemåder af toner og tonehøjder med hensyn til traditionel praksis for “tonearter” i musikken, men den omfatter ikke alle muligheder. Følgende noder er almindelige enharmoniske stavemåder (skråstreger angiver, at noder/toner har samme frekvens, men kan repræsenteres eller “staves” som forskellige tonehøjder):
C#/Db D#/Eb F#/Gb G#/Ab A#/Bb
Naturligvis kan enhver tone teoretisk set hæves eller sænkes et halvt trin (halv tone) eller endda et helt trin (hel tone) med et #- eller b-symbol, og mere avanceret musikteori beskæftiger sig med det, der kaldes double-flats og -sharps.Uden at blive alt for kompliceret eller dybdegående er alle skalaer eller tonearter en samling af halve trin og hele trin, og stavemåden af disse tonehøjder giver den udøvende kunstner fingerpeg om forholdet (dvs. forholdet) mellem de tonehøjder, som komponisten bruger.
- Hertz (Hz)
- Frekvens
- Tone
- Tonehøjde
- A4 (A440)
- Oktaver
- Hele trin (hele toner)
- Halvtonetrin (halvtoner)
Selv-Quiz
- Højden G3 har en grundfrekvens på 196 Hz. Hvad er frekvenserne for tonerne G2 og G4 (en oktav under og over G4) uden at konsultere en tabel?
Supplerende ressourcer
- Lydegenskaber – Khan Academy
- Lyd: Crash Course Physics