Lad os undersøge, hvad der sker, når negative værdier optræder under radikalsymbolet (som radikaland) for terningerødder og kvadratrødder.
I nogle situationer er negative tal under et radikalsymbol OK. F.eks. er 
ikke noget problem, da (-2) – (-2) – (-2) – (-2) = -8, hvilket giver svaret -2. I kubikrodsopgaver er det muligt at gange en negativ værdi med sig selv tre gange og få et negativt svar.
Der opstår imidlertid vanskeligheder, når vi ser på en opgave som 
. Denne kvadratrodsopgave spørger efter et tal ganget med sig selv, som vil give et produkt (svar) på -16. Der er simpelthen ingen måde at gange et tal med sig selv på og få et negativt resultat. Overvej: (4) – (4) = 16 og (-4) – (-4) = 16.
|
CUBE ROOTS:
 |
MEN
|
KVARE ROOTS:
 |
|
Ja, (-2) x (-2) x (-2) x (-2) = -8.
Ingen problemer. |
Nej! (4) x (4) ≠ -16. |
Kvadratrødder er synderne! Vanskelighederne opstår, når man støder på en negativ værdi under en kvadratrod. Det er ikke muligt at kvadrere en værdi (gange den med sig selv) og komme frem til en negativ værdi. Hvad gør vi så?
 |
Kvadratroden af et negativt tal findes ikke blandt mængden af reelle tal.
|
Da problemer med negativer under en kvadratrod først dukkede op, troede matematikerne, at der ikke fandtes en løsning. De så ligninger som x2 + 1 = 0, og de undrede sig over, hvad løsningen 
egentlig betød.
I et forsøg på at løse dette problem “skabte” matematikerne et nyt tal, i, som blev omtalt som et “imaginært tal”, da det ikke var i mængden af “reelle tal”. Dette nye tal blev betragtet med stor skepsis. Det imaginære tal optrådte første gang på tryk i år 1545.
 |
Det imaginære tal “i” er kvadratroden af det negative tal 1. |
Et imaginært tal besidder den unikke egenskab, at når det kvadreres, er resultatet negativt.
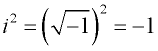
Opmærksomheden henledes på: 
Processen til forenkling af et radikal, der indeholder en negativ faktor, er den samme som normal radikalforenkling. Den eneste forskel er, at 
erstattes med et “i “.
Da forskningen med imaginære tal fortsatte, opdagede man, at de faktisk fyldte et hul i matematikken og tjente et nyttigt formål. De imaginære tal er vigtige for studiet af videnskaber som elektricitet, kvantemekanik, vibrationsanalyse og kartografi.
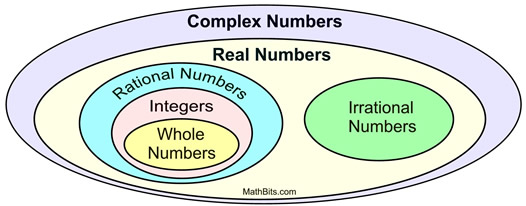
Da det imaginære i blev kombineret med mængden af reelle tal, blev den altomfattende mængde af komplekse tal dannet.
