Wenn du dich in der Natur umsiehst, hast du vielleicht schon komplizierte Pflanzen wie diese bemerkt:


Dieser Farn besteht aus vielen kleinen Blättern, die sich von einem größeren verzweigen.


Dieser Romanesco-Brokkoli besteht aus kleineren Kegelkugeln, die sich spiralförmig um eine größere winden.
Auf den ersten Blick sehen diese Formen sehr komplex aus – aber wenn man genauer hinsieht, stellt man vielleicht fest, dass sie beide einem relativ einfachen Muster folgen: Alle einzelnen Pflanzenteile sehen genauso aus wie die gesamte Pflanze, nur kleiner. Das gleiche Muster wiederholt sich immer wieder, nur in kleinerem Maßstab.
In der Mathematik nennen wir diese Eigenschaft Selbstähnlichkeit, und Formen, die sie aufweisen, werden Fraktale genannt. Sie gehören zu den schönsten und bizarrsten Objekten der gesamten Mathematik.
Um unsere eigenen Fraktale zu erstellen, müssen wir mit einem einfachen Muster beginnen und es dann immer wieder in kleineren Maßstäben wiederholen.
Eines der einfachsten Muster könnte ein Liniensegment sein, von dessen einem Ende zwei weitere Segmente abzweigen. Wenn wir dieses Muster wiederholen, werden auch diese beiden blauen Segmente zwei weitere Verzweigungen an ihren Enden haben.
Sie können die blauen Punkte verschieben, um die Länge und den Winkel aller Verzweigungen zu ändern. Erhöhen Sie dann die Anzahl der Wiederholungen mit dem Schieberegler unten.
Je nach Position der Zweige können Sie völlig unterschiedliche Muster erzeugen – wie der Farn oben, ein Baum oder verschachtelte Fünfecke. Was kannst du noch finden?
Ein weiteres berühmtes Fraktal ist das Sierpinski-Dreieck. In diesem Fall beginnen wir mit einem großen, gleichseitigen Dreieck und schneiden dann wiederholt kleinere Dreiecke aus den verbleibenden Teilen heraus.
Beachte, wie die endgültige Form aus drei identischen Kopien ihrer selbst besteht, und jede dieser Kopien besteht aus noch kleineren Kopien des gesamten Dreiecks! Man könnte ewig in das Dreieck hineinzoomen, und die Muster und Formen würden sich immer wiederholen.
Die Pflanzen am Anfang dieses Kapitels sehen aus wie Fraktale, aber es ist eindeutig unmöglich, echte Fraktale im wirklichen Leben zu erzeugen. Wenn wir das gleiche Muster immer und immer wieder wiederholen, kleiner und kleiner, würden wir schließlich zu Zellen, Molekülen oder Atomen kommen, die nicht mehr geteilt werden können.
Mit Hilfe der Mathematik können wir jedoch über die Eigenschaften nachdenken, die echte Fraktale haben „würden“ – und diese sind sehr überraschend…
Fraktale Dimensionen
Zunächst wollen wir über die Dimension von Fraktalen nachdenken. Eine Linie hat die Dimension . Wenn man sie um den Faktor 2 skaliert, nimmt ihre Länge um den Faktor 21=2 zu. Offensichtlich!
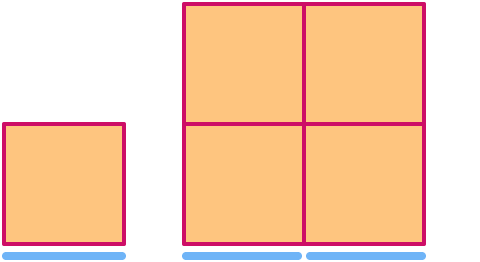
Ein Quadrat hat die Dimension . Bei einer Skalierung um den Faktor 2 vergrößert sich seine Fläche um den Faktor 22=.
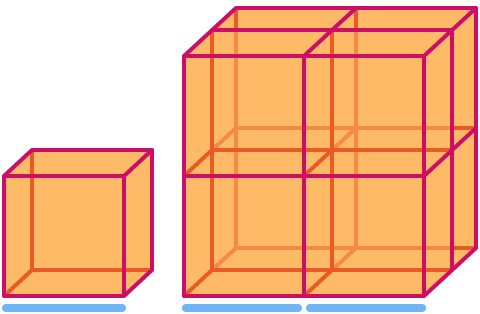
Ein Würfel hat die Dimension . Wenn man ihn um den Faktor 2 skaliert, vergrößert sich sein Volumen um den Faktor 23= . Man beachte, dass der größere Würfel im Bild aus 8 Kopien des kleineren besteht!
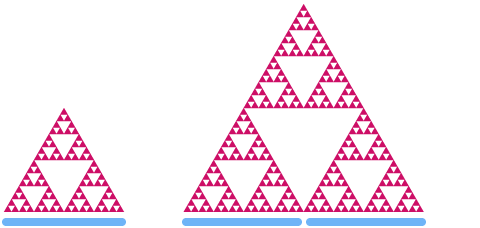
Nun schauen wir uns das Sierpinski-Dreieck an. Wenn wir es um den Faktor 2 skalieren, können wir sehen, dass sich seine „Fläche“ um den Faktor .
vergrößert. Nehmen wir an, dass d die Dimension des Sierpinski-Dreiecks ist. Nach dem gleichen Muster wie oben erhalten wir 2d=3. Mit anderen Worten: d = log23log32 ≈ 1,585…
Aber halt … wie kann etwas eine Dimension haben, die keine ganze Zahl ist? Das scheint unmöglich zu sein, aber das ist nur eine der seltsamen Eigenschaften von Fraktalen. Tatsächlich ist es das, was Fraktalen ihren Namen gibt: Sie haben eine gebrochene Dimension.
Bei jeder Iteration entfernen wir etwas von der Fläche des Sierpinski-Dreiecks. Wenn wir dies unendlich oft tun könnten, bliebe tatsächlich keine Fläche mehr übrig: Deshalb ist das Sierpinski-Dreieck etwas zwischen einer zweidimensionalen Fläche und einer eindimensionalen Linie.
Während viele Fraktale selbstähnlich sind, ist eine bessere Definition, dass Fraktale Formen sind, die eine nicht-ganzzahlige Dimension haben.
Die Koch-Schneeflocke
Es gibt viele Formen in der Natur, die wie Fraktale aussehen. Einige Pflanzen haben wir bereits zu Beginn dieses Kapitels gesehen. Andere gute Beispiele sind Schneeflocken und Eiskristalle:
Um unsere eigene fraktale Schneeflocke zu erzeugen, müssen wir wieder einmal ein einfaches Verfahren finden, das wir immer wieder anwenden können.
Wie beim Sierpinski-Dreieck beginnen wir mit einem einzigen, gleichseitigen Dreieck. Anstatt jedoch bei jedem Schritt kleinere Dreiecke zu entfernen, fügen wir entlang der Kante kleinere Dreiecke hinzu. Die Seitenlänge jedes Dreiecks ist 131412 der Dreiecke des vorherigen Schritts.
Die sich ergebende Form wird als Koch-Schneeflocke bezeichnet, benannt nach dem schwedischen Mathematiker Helge von Koch. Beachte noch einmal, dass kleine Kantenabschnitte der Schneeflocke genauso aussehen wie größere Abschnitte.
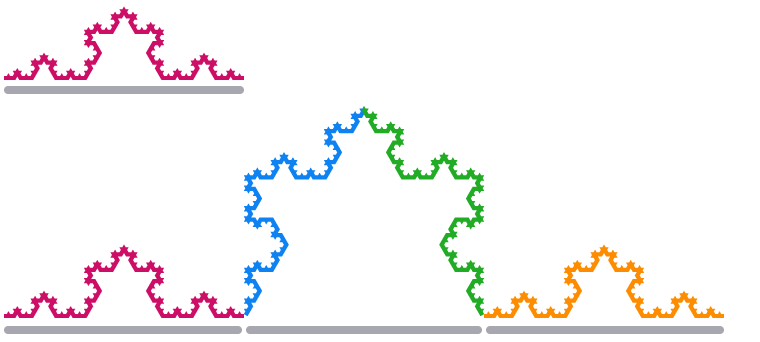
Wenn wir ein Kantensegment der Koch-Schneeflocke um den Faktor 3 skalieren, vervierfacht sich seine Länge.
Wenn wir die gleiche Beziehung zwischen Dimensionen und Skalierungsfaktoren wie oben verwenden, erhalten wir die Gleichung 3d=42d=42d=34d=3. Das bedeutet, dass die Dimension der Kochschen Schneeflocke d=log34≈1,262 ist.
Fläche
Das Erstellen der Koch-Schneeflocken ist fast wie eine rekursive Folge: Wir kennen die Ausgangsform (ein Dreieck), und wir wissen, wie wir von einem Term zum nächsten gelangen (indem wir an jeder Kante weitere Dreiecke hinzufügen):


neue Dreiecke

neue Dreiecke

neue Dreiecke
Nach der ersten Iteration steigt die Anzahl der neu hinzugefügten Dreiecke bei jedem Schritt um den Faktor. Gleichzeitig nimmt die Fläche dieser neuen Dreiecke bei jedem Schritt um den Faktor 1 ab.
Angenommen, das erste Dreieck hat eine Fläche von 1. Dann ist die Gesamtfläche der nächsten drei Dreiecke 3×19=13. Die folgenden Schritte bilden alle eine geometrische Reihearithmetische Reihequadratische Reihe mit dem gemeinsamen Verhältnis 499443.
Mit Hilfe der Formel für die Summe unendlicher geometrischer Reihen können wir berechnen, dass die Gesamtfläche der Schneeflocke Koch
A=1+13×11-491+949-14=85=1 ist.6.
Perimeter
Wir können auch versuchen, den Perimeter der Schneeflocke von Koch zu berechnen. Wie wir bereits gesehen haben, ändert sich die Länge des Umfangs bei jedem Schritt um den Faktor 433414.
Das bedeutet, dass wir wieder eine geometrische Reihe haben – aber in diesem Fall konvergiert sie nicht zu 0und hat keinen ersten Term. Das bedeutet, dass der Umfang der Koch’schen Schneeflocke tatsächlich unendlich lang ist!

Wenn das widersinnig erscheint, erinnere dich einfach daran, dass wir den Umfang bei jedem Schritt mit 43 multiplizieren, und das unendlich oft tun.
Es ist fast undenkbar, dass man eine Form mit einer endlichen Fläche und einem unendlichen Umfang haben kann – aber das ist nur eine der vielen unerwarteten Eigenschaften von Fraktalen.
Kannst du dir noch andere Möglichkeiten ausdenken, um deine eigenen Fraktale zu erstellen?
„Meine Seele dreht sich spiralförmig auf gefrorenen Fraktalen umher…“
Menger Schwamm
Fraktale müssen nicht „flach“ sein, wie viele der obigen Beispiele. Eines der berühmtesten Fraktale, die dreidimensional aussehen, ist der Menger-Schwamm, benannt nach dem Mathematiker Karl Menger, der ihn 1926 erstmals beschrieb.
Wir beginnen mit einem massiven Würfel und bohren immer kleinere Löcher in seine Seiten. Jede neue Iteration von Löchern hat 131214 die Breite der vorherigen Iteration von Löchern.
Ein 3×3×3-Würfel besteht aus 27 kleineren Würfeln, aber hier haben wir einige von ihnen entfernt. Der Menger-Schwamm besteht aus Kopien von sich selbst, die dreimal kleiner sind.
Nun können wir versuchen, die Dimension d des Menger-Schwamms zu berechnen, genau wie wir es oben für die Schneeflocke von Koch getan haben. In diesem Fall erhalten wir 3d=20, oder d=log320≈2.727.
Wenn man sich vorstellt, dass man immer mehr Löcher herausschneidet, unendlich viele Male, würde kein wirkliches Volumen übrig bleiben. Deshalb ist der Würfel auch „nicht ganz“ dreidimensional!
Fraktale Küstenlinien
Eines der Hauptmerkmale aller Fraktale, die wir bisher gesehen haben, ist, dass man immer weiter „heranzoomen“ kann und immer neue Muster findet. Um 1920 erkannte der britische Mathematiker Lewis Fry Richardson, dass dies auch für die Grenzen oder Küstenlinien vieler Länder gilt.
Man beginnt mit der Grundform des Landes und fügt beim Heranzoomen Flusseinläufe, Buchten und Flussmündungen hinzu, dann einzelne Klippen, Felsen, Kieselsteine und so weiter:
Dies ist ein erhebliches Problem, wenn man versucht, die Länge der Grenze eines Landes zu berechnen – wie entscheidet man, wie weit man hineinzoomt und welche Ecken und Winkel man einbezieht?
Eine Möglichkeit, die Länge der Küste Großbritanniens zu messen, ist zum Beispiel, ein langes Lineal zu nehmen, an den Stränden entlangzugehen und dann alle Entfernungen zusammenzuzählen.
Wenn das Lineal ${rulers}km lang ist, müssen wir es ${count} mal benutzen, also erhalten wir eine Gesamtküstenlänge von ${count} × ${Maßstäbe} = ${Anzahl * Maßstäbe}km.
Wir können einfach so weitermachen, mit immer kleineren Maßstäben, und jedes Mal würde unser Ergebnis für die Länge der Küstenlinie ein bisschen länger werden. Genau wie bei der Schneeflocke von Koch scheint es, dass die britische Küste unendlich lang ist! Dies wird oft als das Küstenparadoxon bezeichnet.
Einige Jahrzehnte später stieß der Mathematiker Benoit Mandelbrot bei seiner Arbeit bei IBM in einem ausrangierten Bibliotheksbuch auf die Arbeit von Richardson. Er erkannte ihre Bedeutung und auch, wie sie mit der neueren Forschung über Fraktale und Dimensionen zusammenhängt.
Die Küstenlinie Großbritanniens sieht zwar fraktal aus, ist aber nicht selbstähnlich, wie andere Fraktale, die wir schon gesehen haben. Um ihre Größe zu bestimmen, können wir sie in ein Gitter einzeichnen und die Anzahl der Zellen zählen, mit denen sie sich schneidet.
Zunächst gibt es 88 sich schneidende Zellen. Wenn wir die Küstenlinie um den Faktor 2 skalieren, gibt es 197 sich schneidende Zellen – mehr als doppelt so viele!
Die Größe der Küstenlinie hat sich um den Faktor 19788 erhöht. Wie zuvor bedeutet dies, dass die Dimension der Küstenlinie
d=log219788≈1,16
Wenn wir dies mit größeren Gittern wiederholen, würden wir feststellen, dass die Dimension der britischen Küstenlinie tatsächlich ungefähr 1,21 beträgt. Mandelbrot erkannte, dass diese fraktale Dimension auch ein Maß für die Rauheit einer Form ist – ein neues Konzept, für das er wichtige Anwendungen in vielen anderen Bereichen der Mathematik und der Wissenschaft fand.
Weitere Fraktale in Natur und Technik
Während echte Fraktale in der Natur niemals auftreten können, gibt es viele Objekte, die fast wie Fraktale aussehen. Wir haben bereits Pflanzen, Schneeflocken und Küstenlinien gesehen, und hier sind einige weitere Beispiele:
Gebirge in Zentralasien
Ganges-Delta in Indien
Blitze
Blutgefäße in der Netzhaut
Grand Canyon in den USA
Wolken
Alle diese Objekte mögen völlig zufällig erscheinen, aber genau wie bei Fraktalen gibt es ein zugrundeliegendes Muster, das bestimmt, wie sie geformt werden. Die Mathematik kann uns helfen, die Formen besser zu verstehen, und Fraktale haben Anwendungen in Bereichen wie Medizin, Biologie, Geologie und Meteorologie.
Computergeneriertes fraktales Terrain
Wir können Fraktale auch verwenden, um realistische „Kopien“ der Natur zu erstellen, zum Beispiel als Landschaften und Texturen in Videospielen oder computergenerierten Filmen. Das Wasser, die Berge und die Wolken in diesem Bild wurden vollständig vom Computer mit Hilfe von Fraktalen erzeugt!
Und wir können diesen Prozess sogar umkehren, um digitale Bilder zu komprimieren, um ihre Dateigröße zu verringern. Die ersten Algorithmen wurden von Michael Barnsley und Alan Sloan in den 1980er Jahren entwickelt, und noch heute wird an neuen Algorithmen geforscht.