Logistische Regression

Die logistische Regression (auch Logit-Regression oder Logit-Modell genannt) wurde 1958 vom Statistiker David Cox entwickelt und ist ein Regressionsmodell, bei dem die Antwortvariable Y kategorisch ist. Mit der logistischen Regression lässt sich die Wahrscheinlichkeit einer kategorialen Antwort auf der Grundlage einer oder mehrerer Prädiktorvariablen (X) schätzen. Damit kann man sagen, dass das Vorhandensein eines Prädiktors die Wahrscheinlichkeit eines bestimmten Ergebnisses um einen bestimmten Prozentsatz erhöht (oder verringert). Dieses Lernprogramm behandelt den Fall, dass Y binär ist, d. h. nur zwei Werte annehmen kann, „0“ und „1“, die Ergebnisse wie bestanden/nicht bestanden, gewonnen/verloren, lebendig/tot oder gesund/krank darstellen. Fälle, in denen die abhängige Variable mehr als zwei Ergebniskategorien hat, können mit der multinomialen logistischen Regression analysiert werden, oder, wenn die mehreren Kategorien geordnet sind, mit der ordinalen logistischen Regression. Die Diskriminanzanalyse hat sich jedoch zu einer beliebten Methode für die Mehrklassen-Klassifikation entwickelt, so dass sich unser nächstes Tutorial auf diese Technik für diese Fälle konzentrieren wird.

tl;dr

Dieses Tutorial dient als Einführung in die logistische Regression und deckt1:

1. Replikationsanforderungen: Was Sie benötigen, um die Analyse in diesem Tutorium zu reproduzieren
2. Warum logistische Regression: Warum die logistische Regression?
3. Vorbereitung der Daten: Vorbereiten unserer Daten für die Modellierung
4. Einfache logistische Regression: Vorhersage der Wahrscheinlichkeit einer Reaktion Y mit einer einzelnen Prädiktorvariablen X
5. Multiple logistische Regression: Vorhersage der Reaktionswahrscheinlichkeit Y mit mehreren Prädiktorvariablen
6. Modellbewertung & Diagnostik: Wie gut passt das Modell zu den Daten? Welche Prädiktoren sind am wichtigsten? Sind die Vorhersagen akkurat?

Replikationsanforderungen

Dieses Tutorium nutzt in erster Linie die Default Daten, die vom ISLR Paket bereitgestellt werden. Dabei handelt es sich um einen simulierten Datensatz, der Informationen über zehntausend Kunden enthält, z. B. ob der Kunde säumig ist, ob er Student ist, wie hoch der durchschnittliche Kontostand des Kunden ist und wie hoch sein Einkommen ist. Wir werden auch einige Pakete verwenden, die Funktionen für die Datenmanipulation, die Visualisierung, die Modellierung von Pipelines und das Aufräumen der Modellausgabe bieten.

# Packageslibrary(tidyverse) # data manipulation and visualizationlibrary(modelr) # provides easy pipeline modeling functionslibrary(broom) # helps to tidy up model outputs# Load data (default <- as_tibble(ISLR::Default))## # A tibble: 10,000 × 4## default student balance income## <fctr> <fctr> <dbl> <dbl>## 1 No No 729.5265 44361.625## 2 No Yes 817.1804 12106.135## 3 No No 1073.5492 31767.139## 4 No No 529.2506 35704.494## 5 No No 785.6559 38463.496## 6 No Yes 919.5885 7491.559## 7 No No 825.5133 24905.227## 8 No Yes 808.6675 17600.451## 9 No No 1161.0579 37468.529## 10 No No 0.0000 29275.268## # ... with 9,990 more rows

Warum logistische Regression

Lineare Regression ist im Falle einer qualitativen Antwort nicht geeignet. Why not? Nehmen wir an, wir versuchen, den Gesundheitszustand eines Patienten in der Notaufnahme anhand seiner Symptome vorherzusagen. In diesem vereinfachten Beispiel gibt es drei mögliche Diagnosen: Schlaganfall, Drogenüberdosis und epileptischer Anfall. Wir könnten diese Werte wie folgt als quantitative Antwortvariable Y kodieren:

Mit dieser Kodierung könnte ein lineares Regressionsmodell zur Vorhersage von Y auf der Grundlage einer Reihe von Prädiktoren mit Hilfe der kleinsten Quadrate angepasst werden. Leider impliziert diese Kodierung eine Ordnung der Ergebnisse, indem sie die Drogenüberdosis zwischen Schlaganfall und epileptischem Anfall einordnet und darauf besteht, dass der Unterschied zwischen Schlaganfall und Drogenüberdosis derselbe ist wie der Unterschied zwischen Drogenüberdosis und epileptischem Anfall. In der Praxis gibt es keinen besonderen Grund dafür, dass dies der Fall sein muss. Man könnte zum Beispiel eine ebenso vernünftige Kodierung wählen,

, die eine völlig andere Beziehung zwischen den drei Zuständen implizieren würde. Jede dieser Kodierungen würde zu grundlegend unterschiedlichen linearen Modellen führen, die letztlich zu unterschiedlichen Vorhersagen für die Testbeobachtungen führen würden.

Wenn wir versuchen, einen Kunden auf der Grundlage seines Saldos als Kunde mit hohem bzw. niedrigem Ausfallrisiko zu klassifizieren, könnten wir eine lineare Regression verwenden; die linke Abbildung unten zeigt jedoch, wie die lineare Regression die Ausfallwahrscheinlichkeit vorhersagen würde. Leider sagen wir für Guthaben nahe Null eine negative Ausfallwahrscheinlichkeit voraus; würden wir für sehr große Guthaben eine Vorhersage treffen, würden wir Werte größer als 1 erhalten. Diese Vorhersagen sind nicht sinnvoll, da die tatsächliche Ausfallwahrscheinlichkeit, unabhängig vom Kreditkartenguthaben, zwischen 0 und 1 liegen muss.

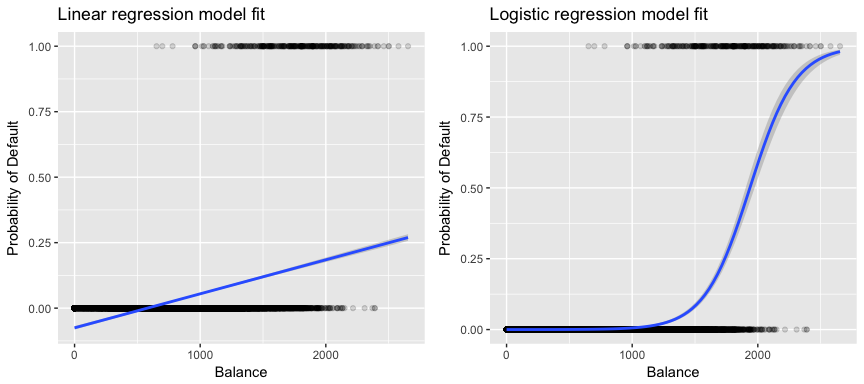
Um dieses Problem zu vermeiden, müssen wir p(X) mit einer Funktion modellieren, die für alle Werte von X Ausgaben zwischen 0 und 1 liefert. Bei der logistischen Regression verwenden wir die logistische Funktion, die in Gl. 1 definiert und in der Abbildung rechts oben dargestellt ist.

Vorbereitung unserer Daten

Wie im Regressionslehrgang werden wir unsere Daten in einen Trainings- (60 %) und einen Testdatensatz (40 %) aufteilen, damit wir beurteilen können, wie gut unser Modell bei einem Datensatz außerhalb der Stichprobe funktioniert.

set.seed(123)sample <- sample(c(TRUE, FALSE), nrow(default), replace = T, prob = c(0.6,0.4))train <- defaulttest <- default

Einfache logistische Regression

Wir passen ein logistisches Regressionsmodell an, um die Wahrscheinlichkeit der Zahlungsunfähigkeit eines Kunden auf der Grundlage seines durchschnittlichen Guthabens vorherzusagen. Die Funktion glm passt verallgemeinerte lineare Modelle an, eine Klasse von Modellen, zu der auch die logistische Regression gehört. Die Syntax der Funktion glm ähnelt der von lm, mit der Ausnahme, dass wir das Argument family = binomial übergeben müssen, um R anzuweisen, eine logistische Regression und nicht eine andere Art von verallgemeinertem linearen Modell auszuführen.

model1 <- glm(default ~ balance, family = "binomial", data = train)

Im Hintergrund verwendet die Funktion glm die maximale Wahrscheinlichkeit, um das Modell anzupassen. Die grundlegende Intuition hinter der Verwendung von Maximum Likelihood zur Anpassung eines logistischen Regressionsmodells ist folgende: Wir suchen nach Schätzungen für und, so dass die vorhergesagte Ausfallwahrscheinlichkeit für jedes Individuum unter Verwendung von Gleichung 1 so genau wie möglich dem beobachteten Ausfallstatus des Individuums entspricht. Mit anderen Worten, wir versuchen, und so zu finden, dass das Einsetzen dieser Schätzungen in das Modell für p(X), das in Gleichung 1 gegeben ist, eine Zahl nahe eins für alle Personen ergibt, die ausgefallen sind, und eine Zahl nahe null für alle Personen, die nicht ausgefallen sind. Diese Intuition lässt sich mit Hilfe einer mathematischen Gleichung formalisieren, die als Likelihood-Funktion bezeichnet wird:

Die Schätzungen und werden so gewählt, dass diese Likelihood-Funktion maximiert wird. Maximum Likelihood ist ein sehr allgemeiner Ansatz, der zur Anpassung vieler nichtlinearer Modelle verwendet wird, die wir in späteren Tutorials untersuchen werden. Das Ergebnis ist eine S-förmige Wahrscheinlichkeitskurve, die unten abgebildet ist (beachten Sie, dass wir unsere Antwortvariable in eine binär codierte Variable umwandeln müssen, um die Anpassungslinie der logistischen Regression darzustellen).

default %>% mutate(prob = ifelse(default == "Yes", 1, 0)) %>% ggplot(aes(balance, prob)) + geom_point(alpha = .15) + geom_smooth(method = "glm", method.args = list(family = "binomial")) + ggtitle("Logistic regression model fit") + xlab("Balance") + ylab("Probability of Default")

Ähnlich wie bei der linearen Regression können wir das Modell mit summary oder glance bewerten. Beachten Sie, dass das Format der Koeffizientenausgabe dem der linearen Regression ähnelt; die Angaben zur Anpassungsgüte am unteren Rand von summary unterscheiden sich jedoch. Dazu später mehr, aber beachten Sie, dass Sie das Wort Abweichung sehen. Die Abweichung entspricht der Berechnung der Summe der Quadrate in der linearen Regression und ist ein Maß für die mangelnde Anpassung an die Daten in einem logistischen Regressionsmodell. Die Nullabweichung stellt den Unterschied zwischen einem Modell mit nur dem Achsenabschnitt (d. h. „ohne Prädiktoren“) und einem gesättigten Modell (einem Modell mit theoretisch perfekter Anpassung) dar. Ziel ist es, dass die Modellabweichung (als Residualabweichung bezeichnet) geringer ist; kleinere Werte bedeuten eine bessere Anpassung. In dieser Hinsicht bietet das Nullmodell eine Grundlage für den Vergleich von Vorhersagemodellen.

summary(model1)## ## Call:## glm(formula = default ~ balance, family = "binomial", data = train)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.2905 -0.1395 -0.0528 -0.0189 3.3346 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.101e+01 4.887e-01 -22.52 <2e-16 ***## balance 5.669e-03 2.949e-04 19.22 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 1723.03 on 6046 degrees of freedom## Residual deviance: 908.69 on 6045 degrees of freedom## AIC: 912.69## ## Number of Fisher Scoring iterations: 8

Bewertung der Koeffizienten

Die nachstehende Tabelle zeigt die Koeffizientenschätzungen und die zugehörigen Informationen, die sich aus der Anpassung eines logistischen Regressionsmodells zur Vorhersage der Ausfallwahrscheinlichkeit = Ja unter Verwendung der Bilanz ergeben. Beachten Sie, dass die Koeffizientenschätzungen der logistischen Regression die Beziehung zwischen der Prädiktor- und der Antwortvariablen auf einer logarithmischen Skala charakterisieren (weitere Einzelheiten finden Sie in Kap. 3 von ISLR1). Wir sehen also, dass ; dies bedeutet, dass ein Anstieg des Guthabens mit einem Anstieg der Ausfallwahrscheinlichkeit verbunden ist. Um genau zu sein, ist ein Anstieg des Saldos um eine Einheit mit einem Anstieg der logarithmischen Wahrscheinlichkeit eines Zahlungsausfalls um 0,0057 Einheiten verbunden.

tidy(model1)## term estimate std.error statistic p.value## 1 (Intercept) -11.006277528 0.488739437 -22.51972 2.660162e-112## 2 balance 0.005668817 0.000294946 19.21985 2.525157e-82

Wir können den Saldokoeffizienten folgendermaßen interpretieren: Für jeden Dollar, um den sich der monatliche Saldo erhöht, steigt die Wahrscheinlichkeit, dass der Kunde in Verzug gerät, um den Faktor 1.0057.

exp(coef(model1))## (Intercept) balance ## 1.659718e-05 1.005685e+00

Viele Aspekte der Koeffizientenausgabe ähneln denen, die bei der Ausgabe der linearen Regression diskutiert wurden. Zum Beispiel können wir die Konfidenzintervalle und die Genauigkeit der Koeffizientenschätzungen messen, indem wir ihre Standardfehler berechnen. Zum Beispiel hat ein p-Wert < 2e-16, was auf eine statistisch signifikante Beziehung zwischen der Bilanz und der Ausfallwahrscheinlichkeit hinweist. Wir können die Standardfehler auch verwenden, um Konfidenzintervalle zu erhalten, wie wir es im Tutorial zur linearen Regression getan haben:

confint(model1)## 2.5 % 97.5 %## (Intercept) -12.007610373 -10.089360652## balance 0.005111835 0.006269411

Vorhersagen treffen

Nachdem die Koeffizienten geschätzt wurden, ist es ein Leichtes, die Ausfallwahrscheinlichkeit für einen bestimmten Kreditkartensaldo zu berechnen. Anhand der Koeffizientenschätzungen unseres Modells können wir mathematisch vorhersagen, dass die Ausfallwahrscheinlichkeit für eine Person mit einem Guthaben von 1.000 $ weniger als 0,5 % beträgt

Wir können die Ausfallwahrscheinlichkeit in R mit der Funktion predict vorhersagen (achten Sie darauf, type = "response" einzuschließen). Hier vergleichen wir die Ausfallwahrscheinlichkeit auf der Grundlage von Guthaben von $1000 und $2000. Wie Sie sehen können, steigt die Ausfallwahrscheinlichkeit bei einem Saldo von 1000 $ auf 2000 $ deutlich an, nämlich von 0,5 % auf 58 %!

predict(model1, data.frame(balance = c(1000, 2000)), type = "response")## 1 2 ## 0.004785057 0.582089269

Mit dem logistischen Regressionsmodell können auch qualitative Prädiktoren verwendet werden. Als Beispiel können wir ein Modell anpassen, das die Variable student verwendet.

model2 <- glm(default ~ student, family = "binomial", data = train)tidy(model2)## term estimate std.error statistic p.value## 1 (Intercept) -3.5534091 0.09336545 -38.05914 0.000000000## 2 studentYes 0.4413379 0.14927208 2.95660 0.003110511

Der mit student = Yes verbundene Koeffizient ist positiv, und der zugehörige p-Wert ist statistisch signifikant. Dies deutet darauf hin, dass Studenten tendenziell eine höhere Ausfallwahrscheinlichkeit haben als Nichtstudenten. Dieses Modell deutet sogar darauf hin, dass die Wahrscheinlichkeit eines Zahlungsausfalls bei Studenten fast doppelt so hoch ist wie bei Nichtstudenten. Im nächsten Abschnitt werden wir jedoch sehen, warum.

predict(model2, data.frame(student = factor(c("Yes", "No"))), type = "response")## 1 2 ## 0.04261206 0.02783019

Mehrfache logistische Regression

Wir können unser Modell, wie in Gl. 1 so erweitern, dass wir eine binäre Antwort unter Verwendung mehrerer Prädiktoren vorhersagen können, wobei p Prädiktoren sind:

Lassen Sie uns nun ein Modell anpassen, das die Wahrscheinlichkeit eines Zahlungsausfalls auf der Grundlage der Variablen Saldo, Einkommen (in Tausend Dollar) und Studentenstatus vorhersagt. Hier gibt es ein überraschendes Ergebnis. Die p-Werte für den Saldo und den Status „Student=Ja“ sind sehr klein, was darauf hindeutet, dass jede dieser Variablen mit der Wahrscheinlichkeit eines Zahlungsausfalls verbunden ist. Der Koeffizient für die Variable „Student“ ist jedoch negativ, was darauf hindeutet, dass Studenten weniger wahrscheinlich säumig sind als Nichtstudenten. Im Gegensatz dazu deutet der Koeffizient für die Studentenvariable in Modell 2, bei dem wir die Ausfallwahrscheinlichkeit nur auf der Grundlage des Studentenstatus vorhersagten, darauf hin, dass Studenten eine höhere Ausfallwahrscheinlichkeit haben. Woran liegt das?

model3 <- glm(default ~ balance + income + student, family = "binomial", data = train)tidy(model3)## term estimate std.error statistic p.value## 1 (Intercept) -1.090704e+01 6.480739e-01 -16.8299277 1.472817e-63## 2 balance 5.907134e-03 3.102425e-04 19.0403764 7.895817e-81## 3 income -5.012701e-06 1.078617e-05 -0.4647343 6.421217e-01## 4 studentYes -8.094789e-01 3.133150e-01 -2.5835947 9.777661e-03

Das rechte Feld der folgenden Abbildung liefert eine Erklärung für diese Diskrepanz. Die Variablen Student und Saldo sind miteinander korreliert. Studenten sind tendenziell höher verschuldet, was wiederum mit einer höheren Ausfallwahrscheinlichkeit verbunden ist. Mit anderen Worten, Studenten haben mit größerer Wahrscheinlichkeit ein hohes Kreditkartenguthaben, das, wie wir aus dem linken Feld der Abbildung unten wissen, mit hohen Ausfallquoten verbunden ist. Obwohl also ein einzelner Student mit einem bestimmten Kreditkartensaldo eine geringere Ausfallwahrscheinlichkeit hat als ein Nichtstudent mit demselben Kreditkartensaldo, bedeutet die Tatsache, dass Studenten insgesamt eher höhere Kreditkartensalden haben, dass Studenten insgesamt eine höhere Ausfallquote haben als Nichtstudenten. Dies ist ein wichtiger Unterschied für ein Kreditkartenunternehmen, das entscheiden muss, wem es einen Kredit anbieten soll. Ein Student ist risikoreicher als ein Nichtstudent, wenn keine Informationen über sein Kreditkartenguthaben verfügbar sind. Dieser Student ist jedoch weniger riskant als ein Nichtstudent mit demselben Kreditsaldo!

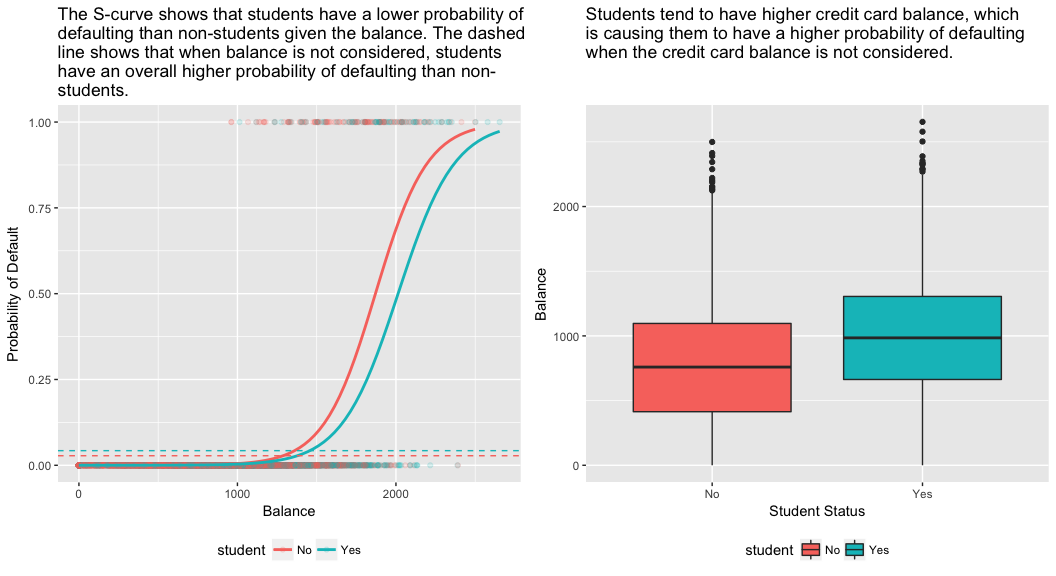
Dieses einfache Beispiel veranschaulicht die Gefahren und Feinheiten, die mit der Durchführung von Regressionen verbunden sind, die nur einen einzigen Prädiktor einbeziehen, wenn andere Prädiktoren ebenfalls relevant sein können. Die mit einem Prädiktor erzielten Ergebnisse können sich erheblich von denen unterscheiden, die mit mehreren Prädiktoren erzielt werden, insbesondere dann, wenn zwischen den Prädiktoren eine Korrelation besteht. Dieses Phänomen wird als Confounding bezeichnet.

Im Falle mehrerer Prädiktorvariablen wollen wir manchmal verstehen, welche Variable den größten Einfluss auf die Vorhersage der Antwortvariable (Y) hat. Wir können dies mit varImp aus dem Paket caret tun. Hier sehen wir, dass der Kontostand mit großem Abstand am wichtigsten ist, während der Studentenstatus weniger wichtig ist, gefolgt vom Einkommen (das sich ohnehin als unbedeutend erwiesen hat (p = .64)).

caret::varImp(model3)## Overall## balance 19.0403764## income 0.4647343## studentYes 2.5835947

Wie zuvor können wir mit diesem Modell leicht Vorhersagen machen. Ein Student mit einem Kreditkartenguthaben von 1.500 $ und einem Einkommen von 40.000 $ hat beispielsweise eine geschätzte Ausfallwahrscheinlichkeit von

Ein Nichtstudent mit demselben Guthaben und Einkommen hat eine geschätzte Ausfallwahrscheinlichkeit von

new.df <- tibble(balance = 1500, income = 40, student = c("Yes", "No"))predict(model3, new.df, type = "response")## 1 2 ## 0.05437124 0.11440288

Wir sehen also, dass bei einem gegebenen Guthaben und Einkommen (obwohl das Einkommen unbedeutend ist) ein Student eine etwa halb so hohe Ausfallwahrscheinlichkeit hat wie ein Nichtstudent.

Modellauswertung & Diagnostik

Bislang wurden drei logistische Regressionsmodelle erstellt und die Koeffizienten untersucht. Es bleiben jedoch einige kritische Fragen offen. Sind die Modelle überhaupt brauchbar? Wie gut passt das Modell zu den Daten?

Goodness-of-Fit

Im Lehrgang zur linearen Regression haben wir gesehen, wie die F-Statistik, die bereinigte und die Residualdiagnose uns darüber informieren, wie gut das Modell zu den Daten passt. Hier sehen wir uns einige Möglichkeiten an, die Anpassungsgüte unserer Logit-Modelle zu beurteilen.

Likelihood Ratio Test

Zunächst können wir einen Likelihood Ratio Test verwenden, um zu beurteilen, ob unsere Modelle die Anpassung verbessern. Das Hinzufügen von Prädiktorvariablen zu einem Modell verbessert fast immer die Modellanpassung (d. h. erhöht die logarithmische Wahrscheinlichkeit und verringert die Modellabweichung im Vergleich zur Nullabweichung), aber es ist notwendig zu testen, ob der beobachtete Unterschied in der Modellanpassung statistisch signifikant ist. Wir können anova verwenden, um diesen Test durchzuführen. Die Ergebnisse zeigen, dass model3 im Vergleich zu model1 die Residualabweichung um mehr als 13 reduziert (zur Erinnerung: ein Ziel der logistischen Regression ist es, ein Modell zu finden, das die Residualabweichung minimiert). Noch wichtiger ist, dass diese Verbesserung mit p = 0,001 statistisch signifikant ist. Dies deutet darauf hin, dass model3 tatsächlich eine bessere Modellanpassung bietet.

anova(model1, model3, test = "Chisq")## Analysis of Deviance Table## ## Model 1: default ~ balance## Model 2: default ~ balance + income + student## Resid. Df Resid. Dev Df Deviance Pr(>Chi) ## 1 6045 908.69 ## 2 6043 895.02 2 13.668 0.001076 **## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pseudo

Im Gegensatz zur linearen Regression mit gewöhnlicher Kleinstquadratschätzung gibt es keine Statistik, die den Anteil der Varianz in der abhängigen Variable erklärt, der durch die Prädiktoren erklärt wird. Es gibt jedoch eine Reihe von Pseudo-Kennzahlen, die von Nutzen sein könnten. Am bemerkenswertesten ist die McFadden-Kennzahl, die wie folgt definiert ist:

, wobei der logarithmische Likelihood-Wert für das angepasste Modell und die logarithmische Likelihood für das Nullmodell mit nur einem Achsenabschnitt als Prädiktor ist. Das Maß reicht von 0 bis knapp unter 1, wobei Werte, die näher bei Null liegen, darauf hinweisen, dass das Modell keine Vorhersagekraft hat. Anders als bei der linearen Regression erreichen die Modelle jedoch selten einen hohen McFadden-Wert. Nach McFaddens eigenen Worten stellen Modelle mit einem McFadden-Pseudowert eine sehr gute Anpassung dar. Wir können die McFadden-Pseudo-Werte für unsere Modelle wie folgt bewerten:

list(model1 = pscl::pR2(model1), model2 = pscl::pR2(model2), model3 = pscl::pR2(model3))## $model1## McFadden ## 0.4726215 ## ## $model2## McFadden ## 0.004898314 ## ## $model3## McFadden ## 0.4805543

Wir sehen, dass Modell 2 einen sehr niedrigen Wert hat, was seine schlechte Anpassung bestätigt. Die Modelle 1 und 3 sind jedoch viel höher, was darauf hindeutet, dass sie einen ziemlich großen Teil der Varianz in den Standarddaten erklären. Außerdem sehen wir, dass Modell 3 die Ergebnisse nur geringfügig verbessert.

Residualbewertung

Denken Sie daran, dass bei der logistischen Regression nicht davon ausgegangen wird, dass die Residuen normalverteilt sind oder dass die Varianz konstant ist. Die Abweichungsresiduen sind jedoch nützlich, um festzustellen, ob einzelne Punkte vom Modell nicht gut erfasst werden. Hier können wir die standardisierten Abweichungsresiduen anpassen, um zu sehen, wie viele davon 3 Standardabweichungen überschreiten. Zuerst extrahieren wir einige nützliche Teile der Modellergebnisse mit augment und fahren dann mit dem Plotten fort.

model1_data <- augment(model1) %>% mutate(index = 1:n())ggplot(model1_data, aes(index, .std.resid, color = default)) + geom_point(alpha = .5) + geom_ref_line(h = 3)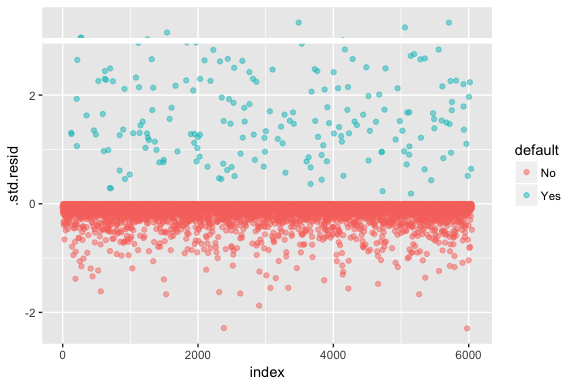

Diejenigen standardisierten Residuen, die 3 überschreiten, stellen mögliche Ausreißer dar und verdienen möglicherweise eine genauere Betrachtung. Wir können nach diesen Residuen filtern, um einen genaueren Blick darauf zu werfen. Wir sehen, dass alle diese Beobachtungen Kunden darstellen, die mit Budgets in Verzug geraten sind, die viel niedriger sind als die der normalen Zahlungsausfälle.

model1_data %>% filter(abs(.std.resid) > 3)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 Yes 1118.7010 -4.664566 0.1752745 3.057432 0.0002841609 0.3857438 0.01508609 3.057867 271## 2 Yes 1119.0972 -4.662320 0.1751742 3.056704 0.0002844621 0.3857448 0.01506820 3.057139 272## 3 Yes 1135.0473 -4.571902 0.1711544 3.027272 0.0002967274 0.3857832 0.01435943 3.027721 1253## 4 Yes 1066.8841 -4.958307 0.1885550 3.151288 0.0002463229 0.3856189 0.01754100 3.151676 1542## 5 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 6 Yes 1143.6805 -4.522962 0.1689933 3.011233 0.0003034789 0.3858039 0.01398491 3.011690 4142## 7 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 8 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709

Ähnlich wie bei der linearen Regression können wir auch einflussreiche Beobachtungen mit Cooks Distanzwerten identifizieren. Hier identifizieren wir die 5 größten Werte.

plot(model1, which = 4, id.n = 5)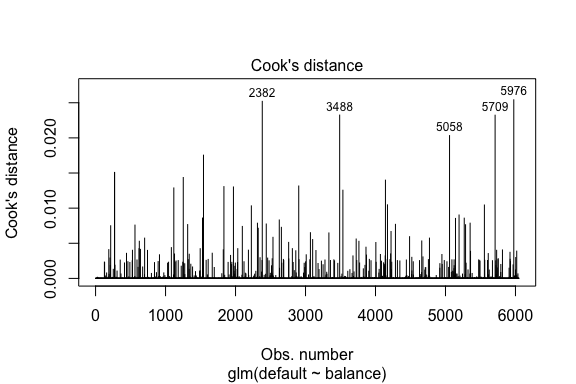

Und auch diese können wir weiter untersuchen. Hier sehen wir, dass zu den fünf einflussreichsten Punkten gehören:

• die Kunden, die mit sehr niedrigen Guthaben in Verzug gerieten, und
• zwei Kunden, die nicht in Verzug gerieten, aber ein Guthaben von über 2.000 $ hatten

Das bedeutet, dass sich Form, Lage und Konfidenzintervall unserer logistischen Regressions-S-Kurve wahrscheinlich verschieben würden, wenn wir diese Beobachtungen entfernen würden (was nicht empfohlen wird).

model1_data %>% top_n(5, .cooksd)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 No 2388.1740 2.531843 0.2413764 -2.284011 0.0039757771 0.3866249 0.02520100 -2.288565 2382## 2 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 3 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 4 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709## 5 No 2391.0077 2.547907 0.2421522 -2.290521 0.0039468742 0.3866185 0.02542145 -2.295054 5976

Validierung der vorhergesagten Werte

Klassifizierungsrate

Bei der Entwicklung von Modellen für die Vorhersage ist der wichtigste Maßstab, wie gut das Modell die Zielvariable bei Beobachtungen außerhalb der Stichprobe vorhersagt. Zunächst müssen wir die geschätzten Modelle zur Vorhersage von Werten in unserem Trainingsdatensatz (train) verwenden. Wenn Sie predict verwenden, müssen Sie type = response einschließen, damit die Vorhersage die Ausfallwahrscheinlichkeit liefert.

test.predicted.m1 <- predict(model1, newdata = test, type = "response")test.predicted.m2 <- predict(model2, newdata = test, type = "response")test.predicted.m3 <- predict(model3, newdata = test, type = "response")

Nun können wir die vorhergesagte Zielvariable mit den beobachteten Werten für jedes Modell vergleichen und sehen, welches Modell am besten abschneidet. Wir können mit der Konfusionsmatrix beginnen, einer Tabelle, die die Klassifizierungsleistung für jedes Modell bei den Testdaten beschreibt. Jeder Quadrant der Tabelle hat eine wichtige Bedeutung. In diesem Fall stehen „Nein“ und „Ja“ in den Zeilen dafür, ob die Kunden säumig waren oder nicht. Die „FALSCH“ und „WAHR“ in den Spalten geben an, ob wir einen Zahlungsausfall des Kunden vorhergesagt haben oder nicht.

• wahr-positiv (Quadrant unten rechts): Dies sind Fälle, in denen wir einen Zahlungsausfall des Kunden vorhergesagt haben und er es auch tat.
• wahr-negativ (Quadrant oben links): Wir haben keinen Zahlungsausfall vorhergesagt, und der Kunde ist nicht ausgefallen.
• Falsch positiv (Quadrant oben rechts): Wir haben ja vorhergesagt, aber der Kunde ist nicht ausgefallen. (Auch bekannt als „Fehler vom Typ I“.)
• Falsch negativ (unten links): Wir haben Nein vorhergesagt, aber sie sind tatsächlich ausgefallen. (Auch bekannt als „Fehler vom Typ II“)

Die Ergebnisse zeigen, dass model1 und model3 sehr ähnlich sind. 96 % der vorhergesagten Beobachtungen sind echte Negative und etwa 1 % sind echte Positive. Beide Modelle haben einen Typ-II-Fehler von weniger als 3 %, d. h. das Modell sagt voraus, dass der Kunde nicht in Verzug gerät, obwohl er es tatsächlich getan hat. Und beide Modelle haben einen Fehler vom Typ I von weniger als 1 %, bei dem das Modell vorhersagt, dass der Kunde in Verzug geraten wird, dies aber nicht der Fall ist. model2 Die Ergebnisse sind bemerkenswert unterschiedlich; dieses Modell sagt die Nicht-Säumigen genau voraus (ein Ergebnis davon, dass 97 % der Daten Nicht-Säumige sind), aber es sagt niemals die Kunden voraus, die säumig sind!

list( model1 = table(test$default, test.predicted.m1 > 0.5) %>% prop.table() %>% round(3), model2 = table(test$default, test.predicted.m2 > 0.5) %>% prop.table() %>% round(3), model3 = table(test$default, test.predicted.m3 > 0.5) %>% prop.table() %>% round(3))## $model1## ## FALSE TRUE## No 0.962 0.003## Yes 0.025 0.010## ## $model2## ## FALSE## No 0.965## Yes 0.035## ## $model3## ## FALSE TRUE## No 0.963 0.003## Yes 0.026 0.009

Wir möchten auch die Fehlklassifizierungs- (auch Fehler-) Raten verstehen (oder wir könnten dies für die Genauigkeitsraten umdrehen). Wir sehen keine große Verbesserung zwischen den Modellen 1 und 3, und obwohl Modell 2 eine niedrige Fehlerquote hat, darf man nicht vergessen, dass es nie genau die Kunden vorhersagt, die tatsächlich in Verzug geraten.

test %>% mutate(m1.pred = ifelse(test.predicted.m1 > 0.5, "Yes", "No"), m2.pred = ifelse(test.predicted.m2 > 0.5, "Yes", "No"), m3.pred = ifelse(test.predicted.m3 > 0.5, "Yes", "No")) %>% summarise(m1.error = mean(default != m1.pred), m2.error = mean(default != m2.pred), m3.error = mean(default != m3.pred))## # A tibble: 1 × 3## m1.error m2.error m3.error## <dbl> <dbl> <dbl>## 1 0.02782697 0.03491019 0.02807994

Wir können einige zusätzliche Erkenntnisse gewinnen, wenn wir uns die Rohwerte (nicht die Prozentwerte) in unserer Konfusionsmatrix ansehen. Betrachten wir zur Veranschaulichung Modell 1. Wir sehen, dass es insgesamt Kunden gibt, die ausgefallen sind. Von der Gesamtzahl der Zahlungsausfälle wurden keine vorhergesagt. Man könnte auch sagen, dass nur ein Teil der Zahlungsausfälle vorhergesagt wurde – dies ist die Präzision (auch als Sensitivität bezeichnet) unseres Modells. Während also die Gesamtfehlerrate niedrig ist, ist auch die Präzisionsrate niedrig, was nicht gut ist!

table(test$default, test.predicted.m1 > 0.5)## ## FALSE TRUE## No 3803 12## Yes 98 40

Bei Klassifizierungsmodellen werden auch die Begriffe Sensitivität und Spezifität verwendet, um die Leistung des Modells zu beschreiben. Wie bereits erwähnt, ist die Sensitivität gleichbedeutend mit der Präzision. Die Spezifität ist jedoch der Prozentsatz der Nicht-Säumigen, die korrekt identifiziert werden (die Genauigkeit wird hier weitgehend durch die Tatsache bestimmt, dass 97 % der Beobachtungen in unseren Daten Nicht-Säumige sind). Die Bedeutung von Sensitivität und Spezifität hängt vom Kontext ab. In diesem Fall ist ein Kreditkartenunternehmen wahrscheinlich eher auf die Sensitivität bedacht, da es sein Risiko verringern möchte. Daher ist es möglicherweise wichtiger, ein Modell so zu optimieren, dass die Sensitivität/Präzision verbessert wird.

Die Empfangsbetriebskennlinie (ROC) ist ein visuelles Maß für die Klassifikatorleistung. Anhand des Anteils positiver Datenpunkte, die korrekt als positiv eingestuft werden, und des Anteils negativer Datenpunkte, die fälschlicherweise als positiv eingestuft werden, wird eine Grafik erstellt, die den Kompromiss zwischen der Rate, mit der man etwas korrekt vorhersagen kann, und der Rate, mit der man etwas falsch vorhersagt, zeigt. Letztendlich geht es uns um die Fläche unter der ROC-Kurve, oder AUC. Diese Kennzahl liegt zwischen 0,50 und 1,00, und Werte über 0,80 zeigen an, dass das Modell die beiden Kategorien, aus denen unsere Zielvariable besteht, gut unterscheiden kann. Wir können die ROC- und AUC-Werte für die Modelle 1 und 2 vergleichen, die sich in ihrer Leistung stark unterscheiden. Wir wollen auf jeden Fall, dass unsere ROC-Diagramme eher wie das von Modell 1 (links) als das von Modell 2 (rechts) aussehen!

library(ROCR)par(mfrow=c(1, 2))prediction(test.predicted.m1, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()prediction(test.predicted.m2, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()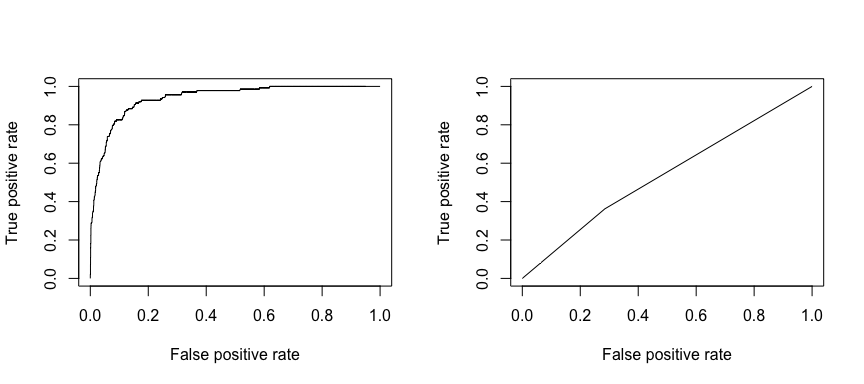

Und um die AUC numerisch zu berechnen, können wir Folgendes verwenden. Denken Sie daran, dass die AUC zwischen 0,50 und 1,00 liegt. Somit ist Modell 2 ein sehr schlechtes Klassifizierungsmodell, während Modell 1 ein sehr gutes Klassifizierungsmodell ist.

# model 1 AUCprediction(test.predicted.m1, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.939932# model 2 AUCprediction(test.predicted.m2, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.5386955

Wir können unsere Modelle weiter „tunen“, um diese Klassifizierungsraten zu verbessern. Wenn Sie Ihre AUC- und ROC-Kurven verbessern können (was bedeutet, dass Sie die Klassifizierungsgenauigkeit verbessern), erzeugen Sie einen „Lift“, d. h. Sie erhöhen die Klassifizierungsgenauigkeit.

Zusätzliche Ressourcen

So können Sie sich mit der logistischen Regression vertraut machen. Denken Sie daran, dass es noch viel mehr zu lernen gibt, und die folgenden Ressourcen helfen Ihnen, mehr zu erfahren:

• An Introduction to Statistical Learning
• Applied Predictive Modeling
• Elements of Statistical Learning