Régression logistique

La régression logistique (alias régression logit ou modèle logit) a été développée par le statisticien David Cox en 1958 et est un modèle de régression où la variable de réponse Y est catégorique. La régression logistique nous permet d’estimer la probabilité d’une réponse catégorique en fonction d’une ou plusieurs variables prédictives (X). Elle permet de dire que la présence d’une variable prédictive augmente (ou diminue) la probabilité d’un résultat donné d’un pourcentage spécifique. Ce tutoriel couvre le cas où Y est binaire, c’est-à-dire qu’il ne peut prendre que deux valeurs, « 0 » et « 1 », qui représentent des résultats tels que réussite/échec, victoire/perte, vie/mort ou santé/maladie. Les cas où la variable dépendante comporte plus de deux catégories de résultats peuvent être analysés au moyen d’une régression logistique multinomiale ou, si les catégories multiples sont ordonnées, d’une régression logistique ordinale. Cependant, l’analyse discriminante est devenue une méthode populaire pour la classification multi-classes, donc notre prochain tutoriel se concentrera sur cette technique pour ces cas.

tl;dr

Ce tutoriel sert d’introduction à la régression logistique et couvre1:

1. Les exigences de reproduction : Ce dont vous aurez besoin pour reproduire l’analyse dans ce tutoriel
2. Pourquoi la régression logistique : Pourquoi utiliser la régression logistique ?
3. Préparer nos données : Préparer nos données pour la modélisation
4. Régression logistique simple : Prédire la probabilité de la réponse Y avec une seule variable prédictive X
5. Régression logistique multiple : Prédire la probabilité de la réponse Y avec plusieurs variables prédictives
6. Évaluation du modèle & diagnostics : Dans quelle mesure le modèle s’adapte-t-il aux données ? Quels sont les prédicteurs les plus importants ? Les prédictions sont-elles précises ?

Exigences de réplication

Ce tutoriel exploite principalement les données Default fournies par le paquet ISLR. Il s’agit d’un ensemble de données simulées contenant des informations sur dix mille clients, comme par exemple si le client a fait défaut, s’il est étudiant, le solde moyen porté par le client et le revenu du client. Nous utiliserons également quelques packages qui fournissent des fonctions de manipulation de données, de visualisation, de modélisation de pipeline et de rangement des sorties de modèles.

# Packageslibrary(tidyverse) # data manipulation and visualizationlibrary(modelr) # provides easy pipeline modeling functionslibrary(broom) # helps to tidy up model outputs# Load data (default <- as_tibble(ISLR::Default))## # A tibble: 10,000 × 4## default student balance income## <fctr> <fctr> <dbl> <dbl>## 1 No No 729.5265 44361.625## 2 No Yes 817.1804 12106.135## 3 No No 1073.5492 31767.139## 4 No No 529.2506 35704.494## 5 No No 785.6559 38463.496## 6 No Yes 919.5885 7491.559## 7 No No 825.5133 24905.227## 8 No Yes 808.6675 17600.451## 9 No No 1161.0579 37468.529## 10 No No 0.0000 29275.268## # ... with 9,990 more rows

Pourquoi la régression logistique

La régression linéaire n’est pas appropriée dans le cas d’une réponse qualitative. Pourquoi pas ? Supposons que nous essayons de prédire l’état médical d’une patiente aux urgences sur la base de ses symptômes. Dans cet exemple simplifié, il y a trois diagnostics possibles : accident vasculaire cérébral, overdose de médicaments et crise d’épilepsie. Nous pourrions envisager de coder ces valeurs comme une variable de réponse quantitative, Y , comme suit :

En utilisant ce codage, les moindres carrés pourraient être utilisés pour ajuster un modèle de régression linéaire afin de prédire Y sur la base d’un ensemble de prédicteurs . Malheureusement, ce codage implique un ordre sur les résultats, plaçant la surdose médicamenteuse entre l’accident vasculaire cérébral et la crise épileptique, et insistant sur le fait que la différence entre l’accident vasculaire cérébral et la surdose médicamenteuse est la même que la différence entre la surdose médicamenteuse et la crise épileptique. En pratique, il n’y a aucune raison particulière pour que ce soit le cas. Par exemple, on pourrait choisir un codage tout aussi raisonnable,

qui impliquerait une relation totalement différente entre les trois conditions. Chacun de ces codages produirait des modèles linéaires fondamentalement différents qui conduiraient en fin de compte à des ensembles différents de prédictions sur les observations de test.

Plus pertinent pour nos données, si nous essayons de classer un client comme un défaillant à haut risque ou à faible risque en fonction de son solde, nous pourrions utiliser la régression linéaire ; cependant, la figure de gauche ci-dessous illustre comment la régression linéaire prédirait la probabilité de défaillance. Malheureusement, pour les soldes proches de zéro, nous prédisons une probabilité négative de défaillance ; si nous devions prédire pour des soldes très importants, nous obtiendrions des valeurs supérieures à 1. Ces prédictions ne sont pas judicieuses, car bien sûr la véritable probabilité de défaillance, indépendamment du solde de la carte de crédit, doit se situer entre 0 et 1.

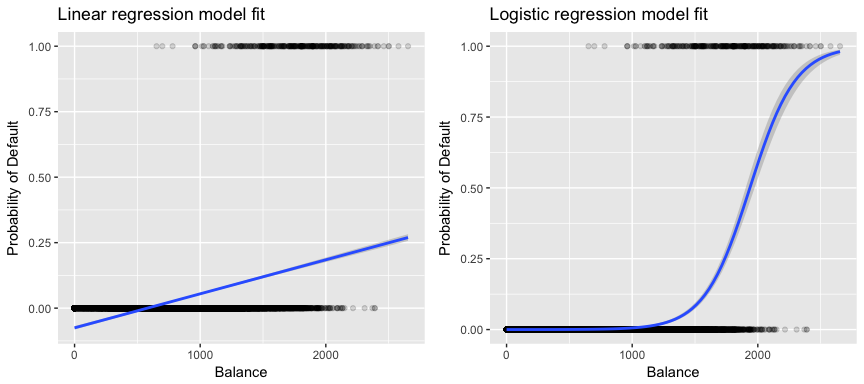
Pour éviter ce problème, nous devons modéliser p(X) à l’aide d’une fonction qui donne des sorties entre 0 et 1 pour toutes les valeurs de X. De nombreuses fonctions répondent à cette description. Dans la régression logistique, nous utilisons la fonction logistique, qui est définie dans l’équation 1 et illustrée dans la figure de droite ci-dessus.

Préparation de nos données

Comme dans le tutoriel sur la régression, nous allons diviser nos données en un ensemble de données d’entraînement (60 %) et de test (40 %) afin de pouvoir évaluer la performance de notre modèle sur un ensemble de données hors échantillon.

set.seed(123)sample <- sample(c(TRUE, FALSE), nrow(default), replace = T, prob = c(0.6,0.4))train <- defaulttest <- default

Régression logistique simple

Nous ajusterons un modèle de régression logistique afin de prédire la probabilité de défaillance d’un client en fonction du solde moyen porté par le client. La fonction glm ajuste des modèles linéaires généralisés, une classe de modèles qui comprend la régression logistique. La syntaxe de la fonction glm est similaire à celle de lm, sauf que nous devons passer l’argument family = binomial afin de dire à R d’exécuter une régression logistique plutôt qu’un autre type de modèle linéaire généralisé.

model1 <- glm(default ~ balance, family = "binomial", data = train)

En arrière-plan, la glm, utilise le maximum de vraisemblance pour ajuster le modèle. L’intuition de base derrière l’utilisation du maximum de vraisemblance pour ajuster un modèle de régression logistique est la suivante : nous cherchons des estimations pour et telles que la probabilité de défaut prédite pour chaque individu, à l’aide de l’équation 1, corresponde aussi étroitement que possible au statut de défaut observé de l’individu. En d’autres termes, nous essayons de trouver et de telle sorte que l’insertion de ces estimations dans le modèle pour p(X), donné dans l’équation 1, donne un nombre proche de un pour tous les individus qui ont fait défaut, et un nombre proche de zéro pour tous les individus qui n’ont pas fait défaut. Cette intuition peut être formalisée à l’aide d’une équation mathématique appelée fonction de vraisemblance :

Les estimations et sont choisies pour maximiser cette fonction de vraisemblance. Le maximum de vraisemblance est une approche très générale qui est utilisée pour ajuster de nombreux modèles non linéaires que nous examinerons dans les prochains tutoriels. Ce qui résulte est une courbe de probabilité en forme de S illustrée ci-dessous (notez que pour tracer la ligne d’ajustement de la régression logistique, nous devons convertir notre variable de réponse en une variable codée binaire).

default %>% mutate(prob = ifelse(default == "Yes", 1, 0)) %>% ggplot(aes(balance, prob)) + geom_point(alpha = .15) + geom_smooth(method = "glm", method.args = list(family = "binomial")) + ggtitle("Logistic regression model fit") + xlab("Balance") + ylab("Probability of Default")

Similaire à la régression linéaire, nous pouvons évaluer le modèle en utilisant summary ou glance. Notez que le format de sortie du coefficient est similaire à ce que nous avons vu dans la régression linéaire ; cependant, les détails de goodness-of-fit au bas de summary diffèrent. Nous y reviendrons plus tard, mais notez simplement que vous voyez le mot déviance. La déviance est analogue aux calculs de la somme des carrés dans la régression linéaire et constitue une mesure de l’absence d’ajustement aux données dans un modèle de régression logistique. La déviance nulle représente la différence entre un modèle ne comportant que l’intercept (ce qui signifie « pas de prédicteurs ») et un modèle saturé (un modèle dont l’ajustement est théoriquement parfait). L’objectif est que la déviance du modèle (notée déviance résiduelle) soit plus faible ; des valeurs plus petites indiquent un meilleur ajustement. À cet égard, le modèle nul fournit une base de référence sur laquelle comparer les modèles prédicteurs.

summary(model1)## ## Call:## glm(formula = default ~ balance, family = "binomial", data = train)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.2905 -0.1395 -0.0528 -0.0189 3.3346 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.101e+01 4.887e-01 -22.52 <2e-16 ***## balance 5.669e-03 2.949e-04 19.22 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 1723.03 on 6046 degrees of freedom## Residual deviance: 908.69 on 6045 degrees of freedom## AIC: 912.69## ## Number of Fisher Scoring iterations: 8

Évaluation des coefficients

Le tableau ci-dessous montre les estimations des coefficients et les informations connexes qui résultent de l’ajustement d’un modèle de régression logistique afin de prédire la probabilité de défaut = Oui en utilisant le solde. Gardez à l’esprit que les estimations des coefficients de la régression logistique caractérisent la relation entre le prédicteur et la variable de réponse sur une échelle logarithmique (voir le chapitre 3 de l’ISLR1 pour plus de détails). Ainsi, nous voyons que ; ceci indique qu’une augmentation du solde est associée à une augmentation de la probabilité de défaut. Pour être précis, une augmentation d’une unité du solde est associée à une augmentation des chances logarithmiques de défaillance de 0,0057 unité.

tidy(model1)## term estimate std.error statistic p.value## 1 (Intercept) -11.006277528 0.488739437 -22.51972 2.660162e-112## 2 balance 0.005668817 0.000294946 19.21985 2.525157e-82

Nous pouvons également interpréter le coefficient de solde comme – pour chaque augmentation d’un dollar du solde mensuel porté, les chances de défaillance du client augmentent d’un facteur de 1.0057.

exp(coef(model1))## (Intercept) balance ## 1.659718e-05 1.005685e+00

Plusieurs aspects de la sortie du coefficient sont similaires à ceux discutés dans la sortie de la régression linéaire. Par exemple, nous pouvons mesurer les intervalles de confiance et la précision des estimations des coefficients en calculant leurs erreurs standard. Par exemple, a une valeur p < 2e-16 suggérant une relation statistiquement significative entre le solde reporté et la probabilité de défaillance. Nous pouvons également utiliser les erreurs standard pour obtenir des intervalles de confiance comme nous l’avons fait dans le tutoriel sur la régression linéaire :

confint(model1)## 2.5 % 97.5 %## (Intercept) -12.007610373 -10.089360652## balance 0.005111835 0.006269411

Faire des prédictions

Une fois les coefficients estimés, il est simple de calculer la probabilité de défaut de paiement pour tout solde de carte de crédit donné. Mathématiquement, en utilisant les estimations des coefficients de notre modèle, nous prédisons que la probabilité de défaut pour un individu avec un solde de 1000 $ est inférieure à 0,5%

Nous pouvons prédire la probabilité de défaut dans R en utilisant la fonction predict (assurez-vous d’inclure type = "response"). Ici, nous comparons la probabilité de défaillance basée sur des soldes de 1000 $ et 2000 $. Comme vous pouvez le voir, lorsque le solde passe de 1000 $ à 2000 $, la probabilité de défaut de paiement augmente de manière significative, de 0,5 % à 58 % !

predict(model1, data.frame(balance = c(1000, 2000)), type = "response")## 1 2 ## 0.004785057 0.582089269

On peut également utiliser des prédicteurs qualitatifs avec le modèle de régression logistique. À titre d’exemple, nous pouvons ajuster un modèle qui utilise la variable student.

model2 <- glm(default ~ student, family = "binomial", data = train)tidy(model2)## term estimate std.error statistic p.value## 1 (Intercept) -3.5534091 0.09336545 -38.05914 0.000000000## 2 studentYes 0.4413379 0.14927208 2.95660 0.003110511

Le coefficient associé à student = Yes est positif, et la valeur p associée est statistiquement significative. Cela indique que les étudiants ont tendance à avoir des probabilités de défaut plus élevées que les non-étudiants. En fait, ce modèle suggère qu’un étudiant a presque deux fois plus de chances de faire défaut que les non-étudiants. Cependant, dans la section suivante, nous verrons pourquoi.

predict(model2, data.frame(student = factor(c("Yes", "No"))), type = "response")## 1 2 ## 0.04261206 0.02783019

Régression logistique multiple

Nous pouvons également étendre notre modèle tel que vu dans l’Eq. 1 de sorte que nous puissions prédire une réponse binaire en utilisant des prédicteurs multiples où sont p prédicteurs :

Allons-y et ajustons un modèle qui prédit la probabilité de défaut de paiement en fonction des variables de solde, de revenu (en milliers de dollars) et de statut d’étudiant. Il y a un résultat surprenant ici. Les valeurs p associées au solde et au statut d’étudiant=Oui sont très faibles, ce qui indique que chacune de ces variables est associée à la probabilité de défaillance. Cependant, le coefficient de la variable étudiant est négatif, ce qui indique que les étudiants sont moins susceptibles d’être en défaut que les non-étudiants. En revanche, le coefficient de la variable étudiant dans le modèle 2, où nous avons prédit la probabilité de défaillance en fonction du seul statut d’étudiant, indique que les étudiants ont une plus grande probabilité de défaillance. Que se passe-t-il ?

model3 <- glm(default ~ balance + income + student, family = "binomial", data = train)tidy(model3)## term estimate std.error statistic p.value## 1 (Intercept) -1.090704e+01 6.480739e-01 -16.8299277 1.472817e-63## 2 balance 5.907134e-03 3.102425e-04 19.0403764 7.895817e-81## 3 income -5.012701e-06 1.078617e-05 -0.4647343 6.421217e-01## 4 studentYes -8.094789e-01 3.133150e-01 -2.5835947 9.777661e-03

Le panneau de droite de la figure ci-dessous fournit une explication à cette divergence. Les variables étudiant et solde sont corrélées. Les étudiants ont tendance à détenir des niveaux d’endettement plus élevés, ce qui est à son tour associé à une plus grande probabilité de défaut. En d’autres termes, les étudiants sont plus susceptibles d’avoir des soldes de carte de crédit importants, qui, comme nous le savons d’après le panneau de gauche de la figure ci-dessous, tendent à être associés à des taux de défaillance élevés. Ainsi, même si un étudiant individuel avec un solde de carte de crédit donné aura tendance à avoir une probabilité de défaillance plus faible qu’un non-étudiant avec le même solde de carte de crédit, le fait que les étudiants dans l’ensemble ont tendance à avoir des soldes de carte de crédit plus élevés signifie que dans l’ensemble, les étudiants ont tendance à défaillir à un taux plus élevé que les non-étudiants. Il s’agit d’une distinction importante pour une société de cartes de crédit qui tente de déterminer à qui elle doit offrir du crédit. Un étudiant est plus risqué qu’un non-étudiant si aucune information sur le solde de sa carte de crédit n’est disponible. Cependant, cet étudiant est moins risqué qu’un non-étudiant ayant le même solde de carte de crédit !

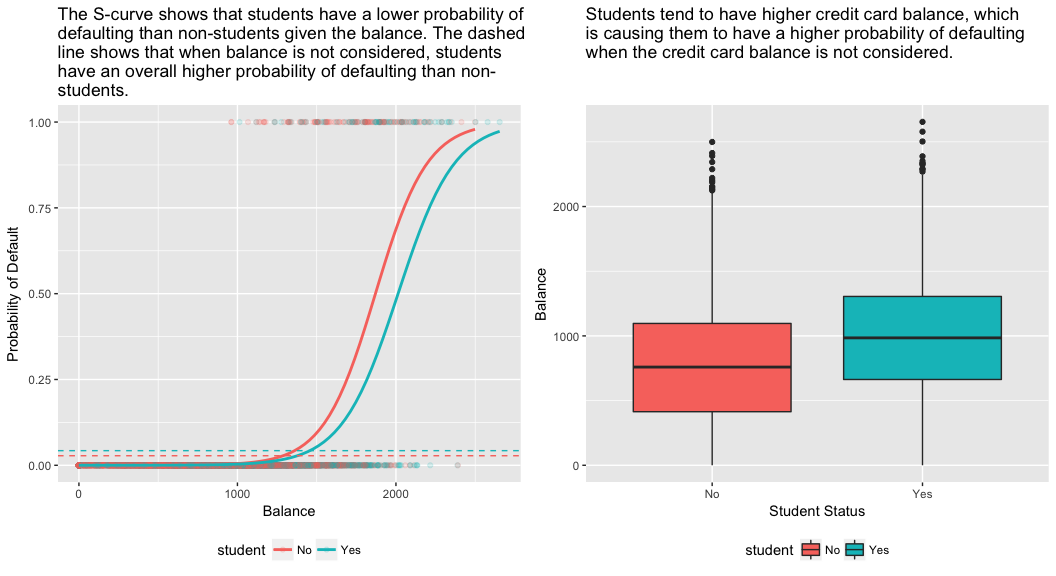
Cet exemple simple illustre les dangers et les subtilités associés à la réalisation de régressions impliquant un seul prédicteur lorsque d’autres prédicteurs peuvent également être pertinents. Les résultats obtenus à l’aide d’un seul prédicteur peuvent être très différents de ceux obtenus à l’aide de plusieurs prédicteurs, en particulier lorsqu’il existe une corrélation entre les prédicteurs. Ce phénomène est connu sous le nom de confusion.

Dans le cas de variables prédicteurs multiples, nous voulons parfois comprendre quelle variable est la plus influente pour prédire la variable réponse (Y). Nous pouvons le faire avec varImp du paquet caret. Ici, nous voyons que le solde est le plus important par une grande marge tandis que le statut d’étudiant est moins important suivi par le revenu (qui s’est avéré être non significatif de toute façon (p = 0,64)).

caret::varImp(model3)## Overall## balance 19.0403764## income 0.4647343## studentYes 2.5835947

Comme avant, nous pouvons facilement faire des prédictions avec ce modèle. Par exemple, un étudiant avec un solde de carte de crédit de 1 500 $ et un revenu de 40 000 $ a une probabilité estimée de défaut de paiement de

Un non-étudiant avec le même solde et le même revenu a une probabilité estimée de défaut de paiement de

new.df <- tibble(balance = 1500, income = 40, student = c("Yes", "No"))predict(model3, new.df, type = "response")## 1 2 ## 0.05437124 0.11440288

On voit donc que pour le solde et le revenu donnés (bien que le revenu soit non significatif), un étudiant a environ la moitié de la probabilité de défaut de paiement qu’un non-étudiant.

Évaluation du modèle &Diagnostics

À ce jour, trois modèles de régression logistique ont été construits et les coefficients ont été examinés. Cependant, certaines questions critiques demeurent. Les modèles sont-ils bons ? Dans quelle mesure le modèle s’adapte-t-il aux données ? Et quelle est la précision des prédictions sur un ensemble de données hors échantillon ?

Goodness-of-Fit

Dans le tutoriel sur la régression linéaire, nous avons vu comment la statistique F, et les diagnostics ajustés , et résiduels nous informent de la qualité de l’ajustement du modèle aux données. Ici, nous allons examiner quelques façons d’évaluer la qualité de l’ajustement de nos modèles logit.

Test du rapport de vraisemblance

Premièrement, nous pouvons utiliser un test du rapport de vraisemblance pour évaluer si nos modèles améliorent l’ajustement. L’ajout de variables prédictives à un modèle améliorera presque toujours l’ajustement du modèle (c’est-à-dire qu’il augmentera la vraisemblance logarithmique et réduira la déviance du modèle par rapport à la déviance nulle), mais il est nécessaire de tester si la différence observée dans l’ajustement du modèle est statistiquement significative. Nous pouvons utiliser anova pour effectuer ce test. Les résultats indiquent que, par rapport à model1, model3 réduit la déviance résiduelle de plus de 13 (rappelez-vous, un objectif de la régression logistique est de trouver un modèle qui minimise les résidus de déviance). Plus important encore, cette amélioration est statistiquement significative à p = 0,001. Cela suggère que model3 fournit un meilleur ajustement du modèle.

anova(model1, model3, test = "Chisq")## Analysis of Deviance Table## ## Model 1: default ~ balance## Model 2: default ~ balance + income + student## Resid. Df Resid. Dev Df Deviance Pr(>Chi) ## 1 6045 908.69 ## 2 6043 895.02 2 13.668 0.001076 **## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pseudo

Contrairement à la régression linéaire avec estimation par les moindres carrés ordinaires, il n’y a pas de statistique qui explique la proportion de la variance de la variable dépendante qui est expliquée par les prédicteurs. Cependant, il existe un certain nombre de pseudo-métriques qui pourraient être utiles. La plus notable est celle de McFadden, qui est définie comme suit :

où est la valeur de vraisemblance logarithmique pour le modèle ajusté et est la vraisemblance logarithmique pour le modèle nul avec seulement une interception comme prédicteur. Cette mesure va de 0 à un peu moins de 1, les valeurs plus proches de zéro indiquant que le modèle n’a aucun pouvoir prédictif. Cependant, contrairement à la régression linéaire, les modèles atteignent rarement une valeur élevée de McFadden . En fait, selon les propres termes de McFadden, les modèles avec un pseudo McFadden représentent un très bon ajustement. Nous pouvons évaluer les valeurs du pseudo de McFadden pour nos modèles avec :

list(model1 = pscl::pR2(model1), model2 = pscl::pR2(model2), model3 = pscl::pR2(model3))## $model1## McFadden ## 0.4726215 ## ## $model2## McFadden ## 0.004898314 ## ## $model3## McFadden ## 0.4805543

Nous voyons que le modèle 2 a une valeur très faible corroborant son mauvais ajustement. Cependant, les modèles 1 et 3 sont beaucoup plus élevés suggérant qu’ils expliquent une bonne partie de la variance des données par défaut. En outre, nous voyons que le modèle 3 n’améliore que très légèrement la

Évaluation des résidus

N’oubliez pas que la régression logistique ne suppose pas que les résidus sont normalement distribués ni que la variance est constante. Cependant, le résidu de la déviance est utile pour déterminer si les points individuels ne sont pas bien ajustés par le modèle. Ici, nous pouvons ajuster les résidus de déviance standardisés pour voir combien dépassent 3 écarts types. Tout d’abord, nous extrayons plusieurs bits utiles des résultats du modèle avec augment, puis nous procédons au tracé.

model1_data <- augment(model1) %>% mutate(index = 1:n())ggplot(model1_data, aes(index, .std.resid, color = default)) + geom_point(alpha = .5) + geom_ref_line(h = 3)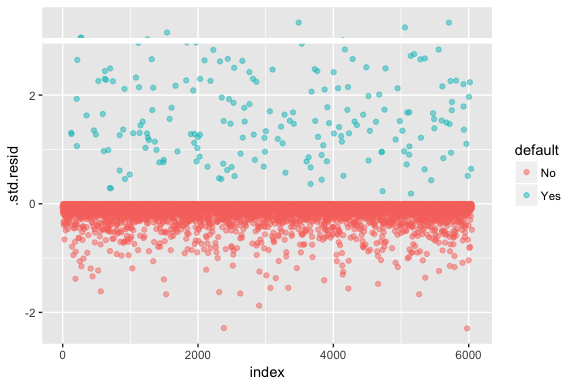

Ces résidus normalisés qui dépassent 3 représentent des aberrations possibles et peuvent mériter une attention plus particulière. Nous pouvons filtrer pour ces résidus afin d’avoir un regard plus attentif. Nous voyons que toutes ces observations représentent des clients qui ont fait défaut avec des budgets beaucoup plus bas que les défaillants normaux.

model1_data %>% filter(abs(.std.resid) > 3)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 Yes 1118.7010 -4.664566 0.1752745 3.057432 0.0002841609 0.3857438 0.01508609 3.057867 271## 2 Yes 1119.0972 -4.662320 0.1751742 3.056704 0.0002844621 0.3857448 0.01506820 3.057139 272## 3 Yes 1135.0473 -4.571902 0.1711544 3.027272 0.0002967274 0.3857832 0.01435943 3.027721 1253## 4 Yes 1066.8841 -4.958307 0.1885550 3.151288 0.0002463229 0.3856189 0.01754100 3.151676 1542## 5 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 6 Yes 1143.6805 -4.522962 0.1689933 3.011233 0.0003034789 0.3858039 0.01398491 3.011690 4142## 7 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 8 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709

Similairement à la régression linéaire, nous pouvons également identifier les observations influentes avec les valeurs de distance de Cook. Ici, nous identifions les 5 plus grandes valeurs.

plot(model1, which = 4, id.n = 5)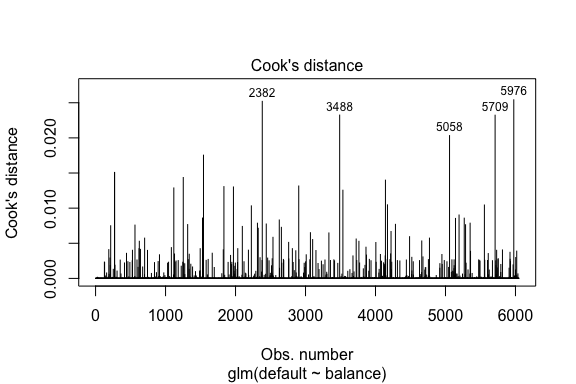

Et nous pouvons également les étudier plus en détail. Ici, nous voyons que les cinq points les plus influents comprennent :

• les clients qui ont fait défaut avec des soldes très bas et
• deux clients qui n’ont pas fait défaut, mais qui avaient des soldes supérieurs à 2 000 $

Cela signifie que si nous devions retirer ces observations (ce qui n’est pas recommandé), la forme, l’emplacement et l’intervalle de confiance de notre courbe en S de régression logistique seraient probablement modifiés.

model1_data %>% top_n(5, .cooksd)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 No 2388.1740 2.531843 0.2413764 -2.284011 0.0039757771 0.3866249 0.02520100 -2.288565 2382## 2 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 3 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 4 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709## 5 No 2391.0077 2.547907 0.2421522 -2.290521 0.0039468742 0.3866185 0.02542145 -2.295054 5976

Validation des valeurs prédites

Taux de classification

Lorsque l’on développe des modèles de prédiction, la métrique la plus critique concerne la façon dont le modèle réussit à prédire la variable cible sur les observations hors échantillon. Tout d’abord, nous devons utiliser les modèles estimés pour prédire les valeurs sur notre ensemble de données d’entraînement (train). Lorsque vous utilisez predict, assurez-vous d’inclure type = response afin que la prédiction renvoie la probabilité de défaut.

test.predicted.m1 <- predict(model1, newdata = test, type = "response")test.predicted.m2 <- predict(model2, newdata = test, type = "response")test.predicted.m3 <- predict(model3, newdata = test, type = "response")

Maintenant, nous pouvons comparer la variable cible prédite par rapport aux valeurs observées pour chaque modèle et voir lequel est le plus performant. Nous pouvons commencer par utiliser la matrice de confusion, qui est un tableau qui décrit les performances de classification de chaque modèle sur les données de test. Chaque quadrant du tableau a une signification importante. Dans ce cas, les « Non » et « Oui » dans les rangées représentent si les clients sont en défaut de paiement ou non. Les « FAUX » et « VRAIS » dans les colonnes représentent si nous avons prédit que les clients seraient en défaut ou non.

• vrais positifs (quadrant inférieur droit) : ce sont les cas dans lesquels nous avons prédit que le client serait en défaut et il l’a fait.
• vrais négatifs (quadrant supérieur gauche) : Nous avons prédit qu’il n’y aurait pas de défaut de paiement, et le client ne l’a pas fait.
• faux positifs (quadrant supérieur droit) : Nous avons prédit oui, mais ils n’ont pas réellement fait défaut. (Également connu sous le nom d' » erreur de type I « .)
• faux négatifs (quadrant inférieur gauche) : Nous avons prédit non, mais ils ont effectivement fait défaut. (Également connu sous le nom d' »erreur de type II ».)

Les résultats montrent que model1 et model3 sont très similaires. 96% des observations prédites sont des vrais négatifs et environ 1% sont des vrais positifs. Les deux modèles ont une erreur de type II de moins de 3 %, dans laquelle le modèle prédit que le client ne fera pas défaut, mais qu’il l’a fait en réalité. Et les deux modèles ont une erreur de type I de moins de 1% dans laquelle les modèles prédisent que le client sera en défaut de paiement mais il ne l’a jamais fait. model2 les résultats sont notablement différents ; ce modèle prédit avec précision les non-défaillants (un résultat de 97% des données étant des non-défaillants) mais ne prédit jamais réellement les clients qui font défaut !

list( model1 = table(test$default, test.predicted.m1 > 0.5) %>% prop.table() %>% round(3), model2 = table(test$default, test.predicted.m2 > 0.5) %>% prop.table() %>% round(3), model3 = table(test$default, test.predicted.m3 > 0.5) %>% prop.table() %>% round(3))## $model1## ## FALSE TRUE## No 0.962 0.003## Yes 0.025 0.010## ## $model2## ## FALSE## No 0.965## Yes 0.035## ## $model3## ## FALSE TRUE## No 0.963 0.003## Yes 0.026 0.009

Nous voulons également comprendre les taux de missclassification (aka erreur) (ou nous pourrions inverser cela pour les taux de précision). Nous ne voyons pas beaucoup d’amélioration entre les modèles 1 et 3 et bien que le modèle 2 ait un faible taux d’erreur, n’oubliez pas qu’il ne prédit jamais avec précision les clients qui sont réellement en défaut.

test %>% mutate(m1.pred = ifelse(test.predicted.m1 > 0.5, "Yes", "No"), m2.pred = ifelse(test.predicted.m2 > 0.5, "Yes", "No"), m3.pred = ifelse(test.predicted.m3 > 0.5, "Yes", "No")) %>% summarise(m1.error = mean(default != m1.pred), m2.error = mean(default != m2.pred), m3.error = mean(default != m3.pred))## # A tibble: 1 × 3## m1.error m2.error m3.error## <dbl> <dbl> <dbl>## 1 0.02782697 0.03491019 0.02807994

Nous pouvons obtenir quelques informations supplémentaires en regardant les valeurs brutes (pas les pourcentages) dans notre matrice de confusion. Regardons le modèle 1 pour l’illustrer. Nous voyons qu’il y a un total de clients qui ont fait défaut. Sur le total des défauts de paiement, aucun n’a été prédit. Nous pourrions également dire que seules les occurrences de défaillance ont été prédites – c’est ce que l’on appelle la précision (également appelée sensibilité) de notre modèle. Ainsi, alors que le taux d’erreur global est faible, le taux de précision est également faible, ce qui n’est pas bon !

table(test$default, test.predicted.m1 > 0.5)## ## FALSE TRUE## No 3803 12## Yes 98 40

Avec les modèles de classification, vous entendrez également les termes sensibilité et spécificité pour caractériser les performances du modèle. Comme mentionné ci-dessus la sensibilité est synonyme de précision. Cependant, la spécificité est le pourcentage de non-défaillants qui sont correctement identifiés, ici (la précision ici est largement déterminée par le fait que 97% des observations dans nos données sont des non-défaillants). L’importance entre la sensibilité et la spécificité dépend du contexte. Dans ce cas, une société de cartes de crédit est susceptible de se préoccuper davantage de la sensibilité, car elle souhaite réduire son risque. Par conséquent, elle peut être plus concernée par le réglage d’un modèle afin d’améliorer sa sensibilité/précision.

La caractéristique opérationnelle de réception (ROC) est une mesure visuelle de la performance du classificateur. En utilisant la proportion de points de données positifs qui sont correctement considérés comme positifs et la proportion de points de données négatifs qui sont considérés à tort comme positifs, nous générons un graphique qui montre le compromis entre le taux auquel vous pouvez prédire correctement quelque chose avec le taux de prédiction incorrecte. En fin de compte, c’est l’aire sous la courbe ROC, ou AUC, qui nous intéresse. Cette mesure va de 0,50 à 1,00, et les valeurs supérieures à 0,80 indiquent que le modèle fait un bon travail de discrimination entre les deux catégories qui composent notre variable cible. Nous pouvons comparer le ROC et l’AUC pour les modèles 1 et 2, qui montrent une forte différence de performance. Nous voulons définitivement que nos tracés ROC ressemblent plus à celui du modèle 1 (gauche) qu’à celui du modèle 2 (droite) !

library(ROCR)par(mfrow=c(1, 2))prediction(test.predicted.m1, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()prediction(test.predicted.m2, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()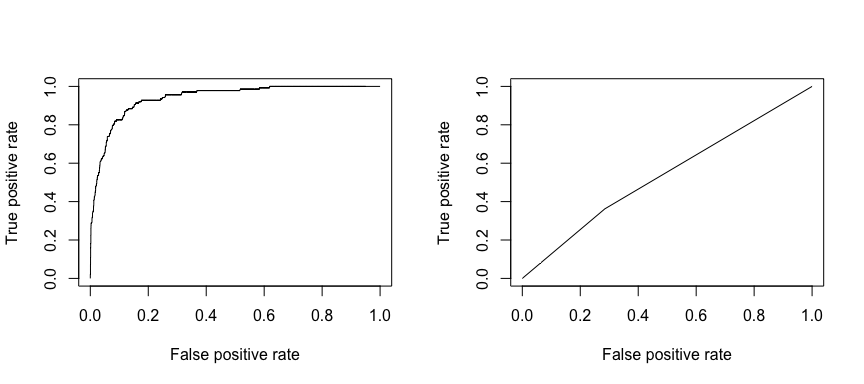

Et pour calculer l’AUC numériquement, nous pouvons utiliser ce qui suit. N’oubliez pas que l’AUC est comprise entre 0,50 et 1,00. Ainsi, le modèle 2 est un très mauvais modèle de classification alors que le modèle 1 est un très bon modèle de classification.

# model 1 AUCprediction(test.predicted.m1, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.939932# model 2 AUCprediction(test.predicted.m2, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.5386955

Nous pouvons continuer à « régler » nos modèles pour améliorer ces taux de classification. Si vous pouvez améliorer vos courbes AUC et ROC (ce qui signifie que vous améliorez les taux de précision de la classification), vous créez un « lift », c’est-à-dire que vous élevez la précision de la classification.

Ressources supplémentaires

Ceci vous permettra d’être opérationnel avec la régression logistique. Gardez à l’esprit qu’il y a beaucoup plus que vous pouvez creuser, donc les ressources suivantes vous aideront à en apprendre davantage :

• An Introduction to Statistical Learning
• Applied Predictive Modeling
• Elements of Statistical Learning

.