Al observar la naturaleza, es posible que hayas notado plantas intrincadas como éstas:


Este helecho está formado por muchas hojas pequeñas que se ramifican de una más grande.


Este brócoli Romanesco está formado por conescubos más pequeños en espiral alrededor de uno más grande.
Inicialmente, parecen formas muy complejas – pero cuando se mira más de cerca, se puede notar que ambos siguen un patrón relativamente simple: todas las partes individuales de las plantas tienen exactamente el mismo aspecto que la planta entera, sólo que más pequeño. El mismo patrón se repite una y otra vez, a escalas más pequeñas.
En matemáticas, llamamos a esta propiedad autosimilaridad, y las formas que la tienen se llaman fractales. Son algunos de los objetos más bellos y más extraños de todas las matemáticas.
Para crear nuestros propios fractales, tenemos que empezar con un patrón simple y luego repetirlo una y otra vez, a escalas más pequeñas.
Uno de los patrones más simples podría ser un segmento de línea, con dos segmentos más que se ramifican en un extremo. Si repetimos este patrón, estos dos segmentos azules también tendrán dos ramas más en sus extremos.
Puedes mover los puntos azules para cambiar la longitud y el ángulo de todas las ramas. A continuación, aumenta el número de iteraciones utilizando el deslizador de abajo.
Dependiendo de la posición de las ramas, puedes hacer patrones completamente diferentes – con el aspecto del helecho de arriba, un árbol o pentágonos anidados. ¿Qué más puedes encontrar?
Otro famoso fractal es el triángulo de Sierpinski. En este caso, empezamos con un gran triángulo equilátero, y luego cortamos repetidamente triángulos más pequeños de las partes restantes.
Nota cómo la forma final está formada por tres copias idénticas de sí misma, ¡y cada una de ellas está formada por copias aún más pequeñas del triángulo entero! Podrías seguir ampliando el triángulo para siempre, y los patrones y las formas siempre seguirían repitiéndose.
Las plantas del principio de este capítulo se parecen a los fractales, pero es claramente imposible crear verdaderos fractales en la vida real. Si seguimos repitiendo el mismo patrón una y otra vez, cada vez más pequeño, acabaríamos llegando a células, moléculas o átomos que ya no se pueden dividir.
Sin embargo, utilizando las matemáticas, podemos pensar en las propiedades que «tendrían» los fractales reales – y éstas son muy sorprendentes…
Dimensiones de los fractales
Primero, pensemos en la dimensión de los fractales. Una línea tiene dimensión . Al escalarla en un factor de 2, su longitud aumenta en un factor de 21=2. Obviamente!
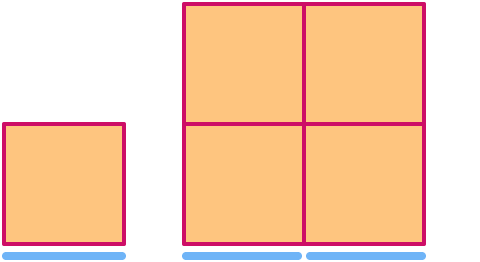
Un cuadrado tiene dimensión . Al escalarlo en un factor 2, su área aumenta en un factor 22= .
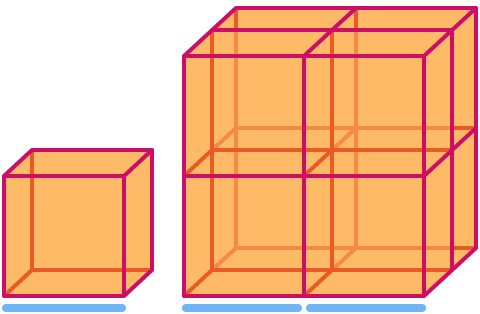
Un cubo tiene dimensión . Si lo escalamos por un factor de 2, su volumen aumenta por un factor de 23= ¡Nota que el cubo más grande de la imagen está formado por 8 copias del más pequeño!
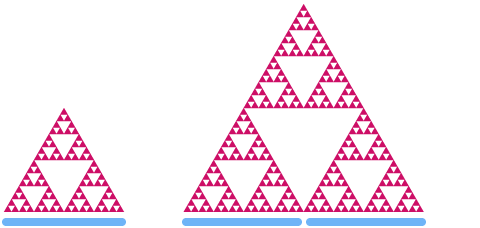
Ahora echemos un vistazo al triángulo de Sierpinski. Si lo escalamos por un factor de 2, puedes ver que su «área» aumenta por un factor de .
Digamos que d es la dimensión del triángulo de Sierpinski. Usando el mismo patrón anterior, obtenemos 2d=3. En otras palabras, d = log23log32 ≈ 1,585…
Pero espera… ¿cómo puede tener algo una dimensión que no sea un número entero? Parece imposible, pero ésta es una de las extrañas propiedades de los fractales. De hecho, esto es lo que da nombre a los fractales: tienen una dimensión fraccionaria.
Con cada iteración, eliminamos parte del área del triángulo de Sierpinski. Si pudiéramos hacer esto infinitas veces, en realidad no quedaría ninguna área: por eso el triángulo de Sierpinski es algo intermedio entre un área bidimensional y una línea unidimensional.
Aunque muchos fractales son autosimilares, una definición mejor es que los fractales son formas que tienen una dimensión no entera.
El copo de nieve de Koch
Hay muchas formas en la naturaleza que parecen fractales. Ya hemos visto algunas plantas al principio de este capítulo. Otros grandes ejemplos son los copos de nieve y los cristales de hielo:
Para crear nuestro propio copo de nieve fractal, una vez más tenemos que encontrar un procedimiento sencillo que podamos aplicar una y otra vez.
Al igual que el triángulo de Sierpinski, vamos a empezar con un único triángulo equilátero. Sin embargo, en lugar de eliminar triángulos más pequeños en cada paso, añadimos triángulos más pequeños a lo largo del borde. La longitud lateral de cada triángulo es 131412 de los triángulos del paso anterior.
La forma resultante se llama copo de nieve de Koch, en honor al matemático sueco Helge von Koch. Observa, una vez más, que las secciones pequeñas del borde del copo de nieve tienen exactamente el mismo aspecto que las secciones más grandes.
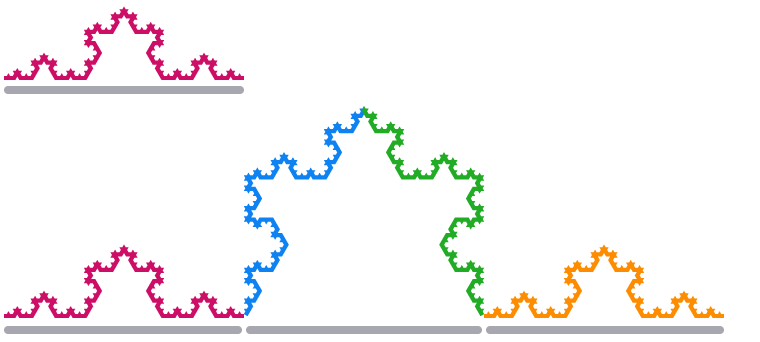
Cuando escalamos un segmento del borde del copo de nieve de Koch por un factor de 3, su longitud se cuadruplica.
Usando la misma relación entre dimensiones y factores de escala que la anterior, obtenemos la ecuación 3d=42d=42d=34d=3. Esto significa que la dimensión del copo de nieve de Koch es d=log34≈1,262.
Área
Crear los copos de nieve de Koch es casi como una secuencia recursiva: conocemos la forma inicial (un triángulo), y sabemos cómo llegar de un término al siguiente (añadiendo más triángulos en cada arista):


nuevos triángulos

nuevos triángulos

nuevos triángulos
Después de la primera iteración, el número de nuevos triángulos añadidos se incrementa en un factor de en cada paso. Al mismo tiempo, el área de estos nuevos triángulos disminuye en un factor de en cada paso.
Digamos que el primer triángulo tiene un área de 1. Entonces el área total de los siguientes tres triángulos es 3×19=13. Los siguientes pasos forman todos ellos una serie geométrica-serie aritmética-serie cuadrática, con razón común 499443.
Utilizando la fórmula de la suma de infinitas series geométricas, podemos calcular que el área total del copo de nieve de Koch es
A=1+13×11-491+949-14=85=1.6.
Perímetro
También podemos intentar calcular el perímetro del copo de nieve de Koch. Como ya hemos visto antes, la longitud del perímetro cambia por un factor de 433414 a cada paso.
Esto significa que, una vez más, tenemos una serie geométrica – pero en este caso, no converge a 0no tiene un primer término. Esto significa que el perímetro del copo de nieve de Koch es en realidad infinitamente largo!

Si esto parece contrario a la intuición, sólo recuerda que multiplicamos el perímetro por 43 en cada paso, y lo hacemos infinitas veces.
Es casi impensable que puedas tener una forma con un área finita y también una circunferencia infinita – pero esta es sólo una de las muchas propiedades inesperadas de los fractales.
¿Se te ocurre alguna otra forma de crear tus propios fractales?
«Mi alma gira en espiral sobre fractales congelados por todas partes…»
Esponja de Menger
Los fractales no tienen por qué ser «planos», como muchos de los ejemplos anteriores. Uno de los fractales más famosos que parecen tridimensionales es la esponja de Menger, llamada así por el matemático Karl Menger que la describió por primera vez en 1926.
Empezamos con un cubo sólido, y perforamos repetidamente agujeros cada vez más pequeños en sus lados. Cada nueva iteración de agujeros tiene 131214 la anchura de la iteración anterior de agujeros.
Un cubo de 3×3×3 está formado por 27 cubos más pequeños, pero aquí hemos eliminado algunos de ellos. La esponja de Menger está formada por copias de sí misma, que son 3 veces más pequeñas.
Ahora podemos intentar calcular la dimensión d de la esponja de Menger igual que hicimos con el copo de nieve de Koch anterior. En este caso obtenemos 3d=20, o d=log320≈2.727.
Si te imaginas recortando más y más agujeros, infinitas veces, no quedaría ningún volumen real. ¡Por eso el cubo no es «del todo» tridimensional!
Las líneas costeras fractales
Una de las características clave de todos los fractales que hemos visto hasta ahora es que se puede «ampliar» eternamente y encontrar siempre nuevos patrones. Alrededor de 1920, el matemático británico Lewis Fry Richardson se dio cuenta de que lo mismo ocurre con la frontera o la costa de muchos países.
Empiezas con la forma básica del país y, a medida que te acercas, añades ensenadas de ríos, bahías y estuarios, luego acantilados individuales, rocas, guijarros, etc:
Este es un problema importante cuando se trata de calcular la longitud de la frontera de un país: ¿cómo se decide hasta dónde acercarse y qué recovecos incluir?
Una forma de medir la longitud de la costa de Gran Bretaña, por ejemplo, es coger una regla larga, recorrer todas sus playas y luego sumar todas las distancias.
Si la regla mide ${rulers}km, tenemos que usarla ${count} veces, por lo que obtenemos una costa total de ${count} × ${rulers} = ${count * rulers}km.
Podemos seguir, con reglas cada vez más pequeñas, y cada vez nuestro resultado para la longitud de la costa sería un poco más largo. Al igual que el copo de nieve de Koch, ¡parece que la costa de Gran Bretaña es infinitamente larga! Esto se llama a menudo la paradoja de la línea de costa.
Unas décadas más tarde, el matemático Benoit Mandelbrot se topó con el trabajo de Richardson en un libro de biblioteca desechado, mientras trabajaba en IBM. Reconoció su importancia, y también su relación con investigaciones más recientes sobre fractales y dimensiones.
La costa de Gran Bretaña ciertamente «parece» fractal, pero no es autosimilar, como otros fractales que hemos visto antes. Para encontrar su tamaño, podemos dibujarla en una cuadrícula y contar el número de celdas con las que se cruza.
Inicialmente, hay 88 celdas de intersección. Si escalamos la línea de costa por un factor de 2, hay 197 celdas de intersección, ¡más del doble!
El tamaño de la línea de costa se ha multiplicado por un factor de 19788. Como antes, esto significa que la dimensión de la línea de costa es
d=log219788≈1,16
Si repetimos esto con cuadrículas más grandes, encontraríamos que la dimensión de la línea de costa de Gran Bretaña es en realidad aproximadamente 1,21. Mandelbrot se dio cuenta de que esta dimensión fractal es también una medida de la rugosidad de una forma -un concepto nuevo, para el que encontró importantes aplicaciones en muchas otras áreas de las matemáticas y la ciencia.
Más fractales en la naturaleza y la tecnología
Aunque los verdaderos fractales nunca pueden aparecer en la naturaleza, hay muchos objetos que parecen casi fractales. Ya hemos visto las plantas, los copos de nieve y las líneas costeras, y aquí hay algunos ejemplos más:
Cordillera en Asia central
Delta del río Ganges en la India
Rayos
Vasos sanguíneos en la retina
El Gran Cañón en los Estados Unidos
Nubes
Todos estos objetos podrían parecer completamente aleatorios, pero, al igual que los fractales, hay un patrón subyacente que determina cómo se forman. Las matemáticas pueden ayudarnos a entender mejor las formas, y los fractales tienen aplicaciones en campos como la medicina, la biología, la geología y la meteorología.
Terreno fractal generado por ordenador
También podemos utilizar los fractales para crear «copias» realistas de la naturaleza, por ejemplo, como paisajes y texturas utilizadas en videojuegos o películas generadas por ordenador. El agua, las montañas y las nubes de esta imagen han sido creadas íntegramente por un ordenador, con la ayuda de fractales.
Incluso podemos invertir este proceso para comprimir imágenes digitales, para reducir su tamaño de archivo. Los primeros algoritmos fueron desarrollados por Michael Barnsley y Alan Sloan en la década de 1980, y aún hoy se siguen investigando otros nuevos.