Eventi dipendenti vs indipendenti
Un paio di post fa ho iniziato a parlare di probabilità. Voglio spendere un po’ più di tempo sull’argomento perché è uno di quei concetti che può essere ovviamente facile un minuto e confuso quello dopo.
Ogni volta che vi avvicinate a un problema di probabilità che coinvolge più di un evento, cominciate col chiedervi se gli eventi sono dipendenti o indipendenti, cioè se un evento altera la probabilità dell’altro evento? Il primo evento che accade cambia il sistema?
(Pescare più carte da un mazzo senza sostituzione è un classico esempio di evento dipendente. Quando peschiamo la prima carta il sistema cambia da 52 opzioni possibili a 51 prima che il secondo evento accada.)
Nella vita reale, gli esseri umani hanno la tendenza a confondere la dipendenza tutto il tempo. Per esempio, si lancia una moneta giusta. Esce testa 10 volte di seguito. Siete certi che il prossimo lancio sarà sicuramente croce… giusto?
Quali sono le probabilità che la prossima moneta sia di nuovo testa?
È sempre 1/2. Il lancio di una moneta è un evento indipendente. In altre parole, il risultato del prossimo lancio non è influenzato da ciò che è successo in precedenza. È come se fosse la prima volta che si lancia la moneta. La probabilità è inalterata.
Perché allora “sembra” che debba essere croce?
Tendiamo a pensare agli eventi insieme, invece che singolarmente. Anche se la probabilità di lanciare teste rimane la stessa per ogni lancio, la probabilità combinata di lanciare 11 teste di fila è piccola.
Calcoliamola.
Abbiamo imparato nella lezione precedente sulla probabilità che quando mettiamo insieme più eventi e vogliamo che si verifichino tutti (lo scenario “e”) dobbiamo moltiplicare le loro probabilità insieme.
Siccome ogni lancio di moneta ha una probabilità di testa pari a 1/2, ho semplicemente bisogno di moltiplicare insieme 1/2 undici volte.
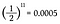
Questa è una probabilità dello 0,05% di lanciare undici teste di fila! Ma prima di tirare un sospiro di sollievo e dire: “Vedi, lo sapevo!”, calcoliamo la probabilità di ottenere invece una coda all’undicesimo lancio.
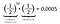
Sì, è vero. È altrettanto probabile lanciare dieci teste seguite da una coda che lanciare undici teste di fila. Infatti, poiché la probabilità individuale di lanciare teste è la stessa della probabilità di lanciare code, ogni disposizione di 11 lanci di moneta avrà la stessa probabilità di 0,0005. Ogni disposizione è ugualmente probabile.
Perciò… perché “sembra” improbabile lanciare dieci teste di fila?
Il malinteso comune non è causato dalla probabilità, ma da un malinteso di combinatoria e permutazioni.
Finora abbiamo stabilito che:
- La probabilità di lanciare testa o croce è ugualmente probabile ad ogni singolo lancio: P(H) = P(T) = 1/2.
- Ogni disposizione unica (permutazione) dei possibili lanci di moneta è ugualmente probabile.
E allora cosa succede?
Comprensione dello spazio campione
Lo spazio campione è semplicemente un elenco di tutte le possibili disposizioni dei risultati (permutazioni). Dato che lo spazio campione per 11 lanci di moneta consecutivi è piuttosto grande, esaminiamo invece un caso più semplice.
Lo spazio campione per quattro lanci di moneta è:

Intuitivamente, potremmo pensare: è più probabile che ci siano 2 teste e 2 code su quattro lanci che tutte le teste o tutte le code.
E questo è vero. Facciamo i conti.
Sappiamo che ognuna delle sedici permutazioni è ugualmente probabile perché P(H) = P(T) = 1/2. Quindi ogni permutazione ha un’uguale probabilità di:

Nota: Poiché lo spazio campione rappresenta tutti i possibili risultati, la somma di tutte le probabilità è sempre uguale a 1 (es. 0,0625 – 16 = 1).
Guardando il nostro spazio campione, quante diverse permutazioni del lancio della moneta risultano in qualsiasi combinazione di 2 teste e 2 code?

Notare che 6 dei 16 risultati possibili risultano in una combinazione due teste/due code. Poiché una qualsiasi di queste sei permutazioni soddisfa i nostri criteri, questo è considerato uno scenario “o” – quindi sommate le probabilità (o semplicemente moltiplicate per 6, dato che sono tutte uguali).
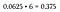
Questo è un 37,5% di probabilità di lanciare una combinazione di 2 teste e 2 code, che è molto più grande della probabilità di lanciare tutte le teste o tutte le code (che rimane 6.Questo è il motivo per cui intuitivamente sappiamo che è più probabile lanciare un numero uguale di teste e di code, che lanciare tutte di un tipo, pur mantenendo il fatto che gli eventi sono indipendenti con lanci individuali e permutazioni con la stessa probabilità di verificarsi.
Permutazioni &Combinazioni
Molto del successo nel calcolo delle probabilità è comprendere a fondo permutazioni e combinazioni. Ecco dove siamo diretti adesso!