Regressione logistica

La regressione logistica (nota anche come regressione logit o modello logit) è stata sviluppata dallo statistico David Cox nel 1958 ed è un modello di regressione dove la variabile di risposta Y è categorica. La regressione logistica ci permette di stimare la probabilità di una risposta categorica in base a una o più variabili predittive (X). Permette di dire che la presenza di un predittore aumenta (o diminuisce) la probabilità di un dato risultato di una specifica percentuale. Questo tutorial copre il caso in cui Y è binario – cioè, dove può assumere solo due valori, “0” e “1”, che rappresentano risultati come passare/fallire, vincere/perdere, vivo/morto o sano/malato. I casi in cui la variabile dipendente ha più di due categorie di risultati possono essere analizzati con la regressione logistica multinomiale o, se le categorie multiple sono ordinate, in regressione logistica ordinale. Tuttavia, l’analisi discriminante è diventata un metodo popolare per la classificazione multiclasse, quindi il nostro prossimo tutorial si concentrerà su questa tecnica per questi casi.

tl;dr

Questo tutorial serve come introduzione alla regressione logistica e copre1:

1. Requisiti per la replica: Di cosa avrete bisogno per riprodurre l’analisi in questo tutorial
2. Perché la regressione logistica: Perché usare la regressione logistica?
3. Preparare i nostri dati: Preparare i nostri dati per la modellazione
4. Regressione logistica semplice: Predire la probabilità della risposta Y con una singola variabile predittiva X
5. Regressione logistica multipla: Previsione della probabilità della risposta Y con più variabili predittive
6. Valutazione del modello & diagnostica: Quanto bene il modello si adatta ai dati? Quali predittori sono più importanti? Le previsioni sono accurate?

Requisiti di replica

Questo tutorial utilizza principalmente i dati Default forniti dal pacchetto ISLR. Si tratta di una serie di dati simulati che contengono informazioni su diecimila clienti, come ad esempio se il cliente è inadempiente, se è uno studente, il saldo medio portato dal cliente e il reddito del cliente. Useremo anche alcuni pacchetti che forniscono funzioni di manipolazione dei dati, di visualizzazione, di modellazione della pipeline e di riordino dell’output del modello.

# Packageslibrary(tidyverse) # data manipulation and visualizationlibrary(modelr) # provides easy pipeline modeling functionslibrary(broom) # helps to tidy up model outputs# Load data (default <- as_tibble(ISLR::Default))## # A tibble: 10,000 × 4## default student balance income## <fctr> <fctr> <dbl> <dbl>## 1 No No 729.5265 44361.625## 2 No Yes 817.1804 12106.135## 3 No No 1073.5492 31767.139## 4 No No 529.2506 35704.494## 5 No No 785.6559 38463.496## 6 No Yes 919.5885 7491.559## 7 No No 825.5133 24905.227## 8 No Yes 808.6675 17600.451## 9 No No 1161.0579 37468.529## 10 No No 0.0000 29275.268## # ... with 9,990 more rows

Perché la regressione logistica

La regressione lineare non è adatta nel caso di una risposta qualitativa. Perché no? Supponiamo che stiamo cercando di prevedere le condizioni mediche di una paziente al pronto soccorso sulla base dei suoi sintomi. In questo esempio semplificato, ci sono tre possibili diagnosi: ictus, overdose di droga e attacco epilettico. Potremmo considerare di codificare questi valori come una variabile di risposta quantitativa, Y, come segue:

Utilizzando questa codifica, i minimi quadrati potrebbero essere utilizzati per adattare un modello di regressione lineare per prevedere Y sulla base di un insieme di predittori. Sfortunatamente, questa codifica implica un ordinamento dei risultati, mettendo l’overdose di droga tra l’ictus e la crisi epilettica, e insistendo sul fatto che la differenza tra l’ictus e l’overdose di droga è la stessa della differenza tra l’overdose di droga e la crisi epilettica. In pratica non c’è nessuna ragione particolare per cui questo debba essere il caso. Per esempio, si potrebbe scegliere una codifica altrettanto ragionevole,

che implicherebbe una relazione totalmente diversa tra le tre condizioni. Ciascuna di queste codifiche produrrebbe modelli lineari fondamentalmente diversi che, in ultima analisi, porterebbero a diverse serie di previsioni sulle osservazioni di prova.

Più rilevante per i nostri dati, se stiamo cercando di classificare un cliente come inadempiente ad alto o a basso rischio in base al suo saldo, potremmo usare la regressione lineare; tuttavia, la figura a sinistra sotto illustra come la regressione lineare predica la probabilità di inadempienza. Sfortunatamente, per saldi vicini allo zero prevediamo una probabilità negativa di insolvenza; se dovessimo prevedere per saldi molto grandi, otterremmo valori maggiori di 1. Queste previsioni non sono sensate, poiché ovviamente la vera probabilità di insolvenza, indipendentemente dal saldo della carta di credito, deve cadere tra 0 e 1.

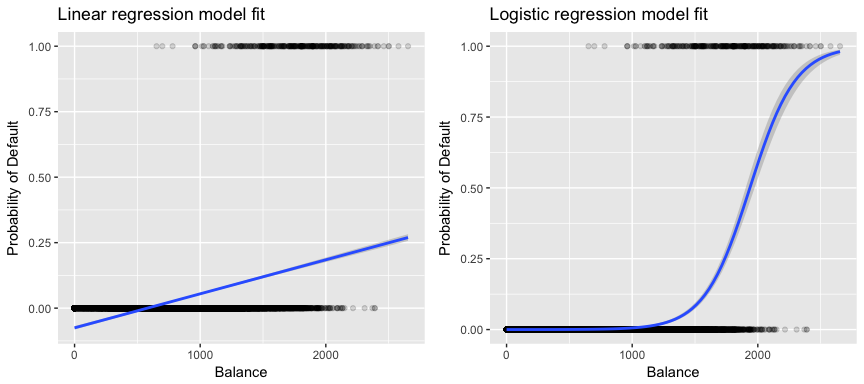
Per evitare questo problema, dobbiamo modellare p(X) usando una funzione che dia risultati tra 0 e 1 per tutti i valori di X. Molte funzioni soddisfano questa descrizione. Nella regressione logistica, usiamo la funzione logistica, che è definita nell’Eq. 1 e illustrata nella figura in alto a destra.

Preparazione dei nostri dati

Come nel tutorial sulla regressione, divideremo i nostri dati in un set di dati di allenamento (60%) e di test (40%) in modo da poter valutare come il nostro modello si comporta su un set di dati fuori campione.

set.seed(123)sample <- sample(c(TRUE, FALSE), nrow(default), replace = T, prob = c(0.6,0.4))train <- defaulttest <- default

Regressione logistica semplice

Modelleremo un modello di regressione logistica per prevedere la probabilità di insolvenza di un cliente in base al suo saldo medio. La funzione glm adatta modelli lineari generalizzati, una classe di modelli che include la regressione logistica. La sintassi della funzione glm è simile a quella di lm, eccetto che dobbiamo passare l’argomento family = binomial per dire a R di eseguire una regressione logistica piuttosto che qualche altro tipo di modello lineare generalizzato.

model1 <- glm(default ~ balance, family = "binomial", data = train)

In fondo la glm, usa la massima verosimiglianza per adattare il modello. L’intuizione di base dietro l’uso della massima verosimiglianza per adattare un modello di regressione logistica è la seguente: cerchiamo stime per e tali che la probabilità di default prevista per ogni individuo, usando l’Eq. 1, corrisponda il più possibile allo stato di default osservato dell’individuo. In altre parole, cerchiamo di trovare e tale che inserendo queste stime nel modello per p(X), dato dall’Eq. 1, si ottenga un numero vicino a uno per tutti gli individui che sono andati in default e un numero vicino a zero per tutti gli individui che non lo hanno fatto. Questa intuizione può essere formalizzata usando un’equazione matematica chiamata funzione di verosimiglianza:

Le stime e sono scelte per massimizzare questa funzione di verosimiglianza. La massima verosimiglianza è un approccio molto generale che viene utilizzato per adattare molti dei modelli non lineari che esamineremo nei futuri tutorial. Il risultato è una curva di probabilità a forma di S illustrata qui sotto (si noti che per tracciare la linea di adattamento della regressione logistica dobbiamo convertire la nostra variabile di risposta in una variabile binaria codificata).

default %>% mutate(prob = ifelse(default == "Yes", 1, 0)) %>% ggplot(aes(balance, prob)) + geom_point(alpha = .15) + geom_smooth(method = "glm", method.args = list(family = "binomial")) + ggtitle("Logistic regression model fit") + xlab("Balance") + ylab("Probability of Default")

Similmente alla regressione lineare possiamo valutare il modello usando summary o glance. Notate che il formato di output dei coefficienti è simile a quello che abbiamo visto nella regressione lineare; tuttavia, i dettagli sulla bontà dell’adattamento in fondo a summary sono diversi. Ne parleremo più avanti, ma notate solo che vedete la parola devianza. La devianza è analoga ai calcoli della somma dei quadrati nella regressione lineare ed è una misura della mancanza di adattamento ai dati in un modello di regressione logistica. La devianza nulla rappresenta la differenza tra un modello con solo l’intercetta (che significa “senza predittori”) e un modello saturo (un modello con un adattamento teoricamente perfetto). L’obiettivo è che la devianza del modello (nota come devianza residua) sia più bassa; valori più piccoli indicano un migliore adattamento. In questo senso, il modello nullo fornisce una linea di base su cui confrontare i modelli predittivi.

summary(model1)## ## Call:## glm(formula = default ~ balance, family = "binomial", data = train)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.2905 -0.1395 -0.0528 -0.0189 3.3346 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.101e+01 4.887e-01 -22.52 <2e-16 ***## balance 5.669e-03 2.949e-04 19.22 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 1723.03 on 6046 degrees of freedom## Residual deviance: 908.69 on 6045 degrees of freedom## AIC: 912.69## ## Number of Fisher Scoring iterations: 8

Valutazione dei coefficienti

La tabella sottostante mostra le stime dei coefficienti e le informazioni correlate che risultano dal montaggio di un modello di regressione logistica per prevedere la probabilità di default = Sì usando l’equilibrio. Si tenga presente che le stime dei coefficienti della regressione logistica caratterizzano la relazione tra il predittore e la variabile di risposta su una scala log-odds (si veda il capitolo 3 di ISLR1 per maggiori dettagli). Così, vediamo che ; questo indica che un aumento del saldo è associato a un aumento della probabilità di default. Per essere precisi, un aumento di un’unità del saldo è associato a un aumento delle probabilità logiche di insolvenza di 0,0057 unità.

tidy(model1)## term estimate std.error statistic p.value## 1 (Intercept) -11.006277528 0.488739437 -22.51972 2.660162e-112## 2 balance 0.005668817 0.000294946 19.21985 2.525157e-82

Possiamo ulteriormente interpretare il coefficiente del saldo come – per ogni dollaro di aumento del saldo mensile portato, la probabilità di insolvenza del cliente aumenta di un fattore 1.0057.

exp(coef(model1))## (Intercept) balance ## 1.659718e-05 1.005685e+00

Molti aspetti dell’output del coefficiente sono simili a quelli discussi nell’output della regressione lineare. Per esempio, possiamo misurare gli intervalli di confidenza e la precisione delle stime dei coefficienti calcolando i loro errori standard. Per esempio, ha un p-value < 2e-16 che suggerisce una relazione statisticamente significativa tra il saldo riportato e la probabilità di default. Possiamo anche usare gli errori standard per ottenere intervalli di confidenza come abbiamo fatto nel tutorial sulla regressione lineare:

confint(model1)## 2.5 % 97.5 %## (Intercept) -12.007610373 -10.089360652## balance 0.005111835 0.006269411

Fare previsioni

Una volta che i coefficienti sono stati stimati, è semplice calcolare la probabilità di default per ogni dato saldo della carta di credito. Matematicamente, usando le stime dei coefficienti del nostro modello, prevediamo che la probabilità di insolvenza per un individuo con un saldo di 1.000 dollari è inferiore allo 0,5%

Possiamo prevedere la probabilità di insolvenza in R usando la funzione predict (assicuratevi di includere type = "response"). Qui confrontiamo la probabilità di insolvenza sulla base di saldi di $1000 e $2000. Come potete vedere, man mano che il saldo passa da 1000 a 2000 dollari, la probabilità di insolvenza aumenta significativamente, dallo 0,5% al 58%!

predict(model1, data.frame(balance = c(1000, 2000)), type = "response")## 1 2 ## 0.004785057 0.582089269

Si possono anche usare predittori qualitativi con il modello di regressione logistica. Come esempio, possiamo adattare un modello che utilizza la variabile student.

model2 <- glm(default ~ student, family = "binomial", data = train)tidy(model2)## term estimate std.error statistic p.value## 1 (Intercept) -3.5534091 0.09336545 -38.05914 0.000000000## 2 studentYes 0.4413379 0.14927208 2.95660 0.003110511

Il coefficiente associato a student = Yes è positivo, e il p-value associato è statisticamente significativo. Questo indica che gli studenti tendono ad avere maggiori probabilità di default rispetto ai non studenti. Infatti, questo modello suggerisce che uno studente ha quasi il doppio delle probabilità di essere inadempiente rispetto ai non studenti. Tuttavia, nella prossima sezione vedremo perché.

predict(model2, data.frame(student = factor(c("Yes", "No"))), type = "response")## 1 2 ## 0.04261206 0.02783019

Regressione logistica multipla

Possiamo anche estendere il nostro modello come visto in Eq. 1 in modo da poter predire una risposta binaria usando predittori multipli dove sono p predittori:

Andiamo avanti e adattiamo un modello che predice la probabilità di insolvenza in base al saldo, al reddito (in migliaia di dollari), e alle variabili di stato degli studenti. Qui c’è un risultato sorprendente. I valori p associati al saldo e allo stato di studente=Sì sono molto piccoli, indicando che ciascuna di queste variabili è associata alla probabilità di insolvenza. Tuttavia, il coefficiente per la variabile studente è negativo, indicando che gli studenti hanno meno probabilità di essere inadempienti rispetto ai non studenti. Al contrario, il coefficiente per la variabile studente nel modello 2, dove abbiamo previsto la probabilità di insolvenza basandoci solo sullo stato di studente, indica che gli studenti hanno una maggiore probabilità di insolvenza. Cosa succede?

model3 <- glm(default ~ balance + income + student, family = "binomial", data = train)tidy(model3)## term estimate std.error statistic p.value## 1 (Intercept) -1.090704e+01 6.480739e-01 -16.8299277 1.472817e-63## 2 balance 5.907134e-03 3.102425e-04 19.0403764 7.895817e-81## 3 income -5.012701e-06 1.078617e-05 -0.4647343 6.421217e-01## 4 studentYes -8.094789e-01 3.133150e-01 -2.5835947 9.777661e-03

Il pannello di destra della figura sottostante fornisce una spiegazione per questa discrepanza. Le variabili studente e saldo sono correlate. Gli studenti tendono a detenere livelli più alti di debito, che è a sua volta associato a una maggiore probabilità di insolvenza. In altre parole, gli studenti hanno maggiori probabilità di avere grandi saldi di carte di credito, che, come sappiamo dal pannello di sinistra della figura sottostante, tendono ad essere associati ad alti tassi di insolvenza. Quindi, anche se un singolo studente con un dato saldo della carta di credito tenderà ad avere una probabilità di insolvenza inferiore a quella di un non studente con lo stesso saldo della carta di credito, il fatto che gli studenti nel complesso tendano ad avere saldi di carte di credito più alti significa che nel complesso gli studenti tendono ad essere insolventi ad un tasso più alto dei non studenti. Questa è una distinzione importante per una compagnia di carte di credito che sta cercando di determinare a chi offrire credito. Uno studente è più rischioso di un non studente se non sono disponibili informazioni sul saldo della carta di credito dello studente. Tuttavia, quello studente è meno rischioso di un non studente con lo stesso saldo della carta di credito!

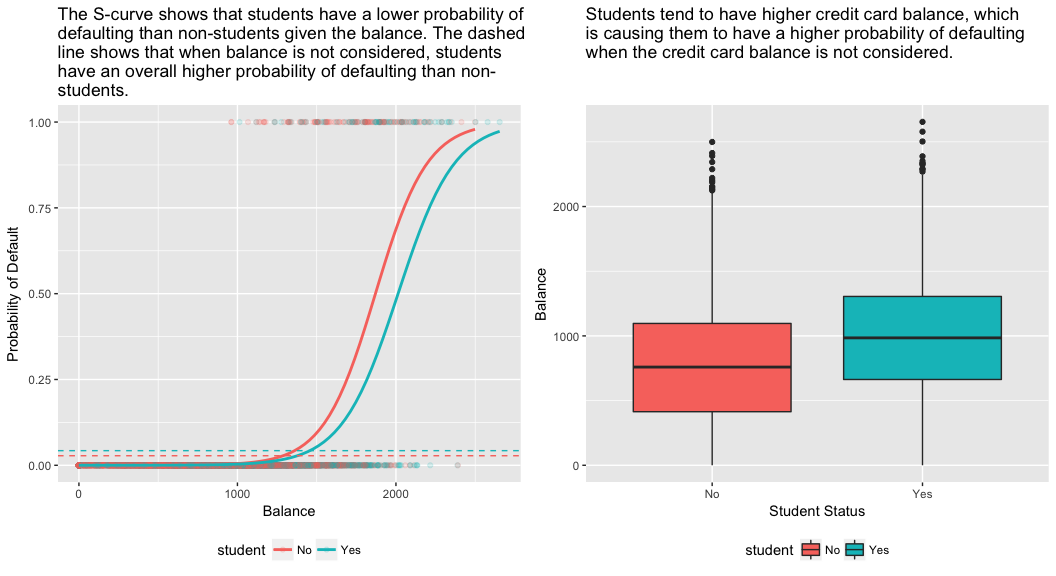
Questo semplice esempio illustra i pericoli e le sottigliezze associate all’esecuzione di regressioni che coinvolgono solo un singolo predittore quando anche altri predittori possono essere rilevanti. I risultati ottenuti usando un solo predittore possono essere molto diversi da quelli ottenuti usando più predittori, specialmente quando c’è correlazione tra i predittori. Questo fenomeno è noto come confondimento.

Nel caso di più variabili predittive a volte vogliamo capire quale variabile è la più influente nel predire la variabile risposta (Y). Possiamo farlo con varImp del pacchetto caret. Qui, vediamo che l’equilibrio è il più importante con un ampio margine, mentre lo status di studente è meno importante seguito dal reddito (che è risultato comunque insignificante (p = .64)).

caret::varImp(model3)## Overall## balance 19.0403764## income 0.4647343## studentYes 2.5835947

Come prima, possiamo facilmente fare previsioni con questo modello. Per esempio, uno studente con un saldo della carta di credito di 1.500 dollari e un reddito di 40.000 dollari ha una probabilità stimata di insolvenza di

Un non studente con lo stesso saldo e lo stesso reddito ha una probabilità stimata di insolvenza di

new.df <- tibble(balance = 1500, income = 40, student = c("Yes", "No"))predict(model3, new.df, type = "response")## 1 2 ## 0.05437124 0.11440288

Così, vediamo che per un dato saldo e reddito (sebbene il reddito sia insignificante) uno studente ha circa la metà della probabilità di insolvenza di un non studente.

Valutazione del modello & Diagnostica

Finora sono stati costruiti tre modelli di regressione logistica e sono stati esaminati i coefficienti. Tuttavia, rimangono alcune domande critiche. I modelli sono validi? Quanto bene il modello si adatta ai dati? E quanto sono accurate le previsioni su un set di dati fuori campione?

Goodness-of-Fit

Nel tutorial sulla regressione lineare abbiamo visto come la statistica F, la rettifica e la diagnostica dei residui ci informano su quanto bene il modello si adatti ai dati. Qui, vedremo alcuni modi per valutare la bontà dell’adattamento dei nostri modelli logit.

Test del rapporto di verosimiglianza

Primo, possiamo usare un test del rapporto di verosimiglianza per valutare se i nostri modelli stanno migliorando l’adattamento. L’aggiunta di variabili predittive a un modello migliorerà quasi sempre l’adattamento del modello (cioè aumenterà la probabilità logica e ridurrà la devianza del modello rispetto alla devianza nulla), ma è necessario verificare se la differenza osservata nell’adattamento del modello è statisticamente significativa. Possiamo usare anova per eseguire questo test. I risultati indicano che, rispetto a model1, model3 riduce la devianza residua di oltre 13 (ricordate, un obiettivo della regressione logistica è quello di trovare un modello che minimizzi i residui di devianza). Ancora più importante, questo miglioramento è statisticamente significativo a p = 0,001. Questo suggerisce che model3 fornisce un migliore adattamento del modello.

anova(model1, model3, test = "Chisq")## Analysis of Deviance Table## ## Model 1: default ~ balance## Model 2: default ~ balance + income + student## Resid. Df Resid. Dev Df Deviance Pr(>Chi) ## 1 6045 908.69 ## 2 6043 895.02 2 13.668 0.001076 **## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pseudo

A differenza della regressione lineare con stima ordinaria dei minimi quadrati, non esiste una statistica che spieghi la proporzione di varianza nella variabile dipendente che è spiegata dai predittori. Tuttavia, ci sono un certo numero di pseudo metriche che potrebbero essere utili. Il più notevole è McFadden’s , che è definito come

dove è il valore di verosimiglianza log per il modello montato ed è la verosimiglianza log per il modello nullo con solo un’intercetta come predittore. La misura varia da 0 a poco meno di 1, con valori più vicini a zero che indicano che il modello non ha potere predittivo. Tuttavia, a differenza della regressione lineare, i modelli raramente raggiungono un alto McFadden . Infatti, nelle parole di McFadden, i modelli con uno pseudo McFadden rappresentano un ottimo adattamento. Possiamo valutare i valori dello pseudo di McFadden per i nostri modelli con:

list(model1 = pscl::pR2(model1), model2 = pscl::pR2(model2), model3 = pscl::pR2(model3))## $model1## McFadden ## 0.4726215 ## ## $model2## McFadden ## 0.004898314 ## ## $model3## McFadden ## 0.4805543

Vediamo che il modello 2 ha un valore molto basso che conferma il suo scarso adattamento. Tuttavia, i modelli 1 e 3 sono molto più alti, suggerendo che spiegano una discreta quantità di varianza nei dati di default. Inoltre, vediamo che il modello 3 migliora solo leggermente la valutazione

Residuale

Si tenga presente che la regressione logistica non presuppone che i residui siano normalmente distribuiti né che la varianza sia costante. Tuttavia, il residuo della devianza è utile per determinare se i singoli punti non sono ben adattati dal modello. Qui possiamo adattare i residui di devianza standardizzati per vedere quanti superano le 3 deviazioni standard. Prima estraiamo diversi bit utili dei risultati del modello con augment e poi procediamo a tracciare.

model1_data <- augment(model1) %>% mutate(index = 1:n())ggplot(model1_data, aes(index, .std.resid, color = default)) + geom_point(alpha = .5) + geom_ref_line(h = 3)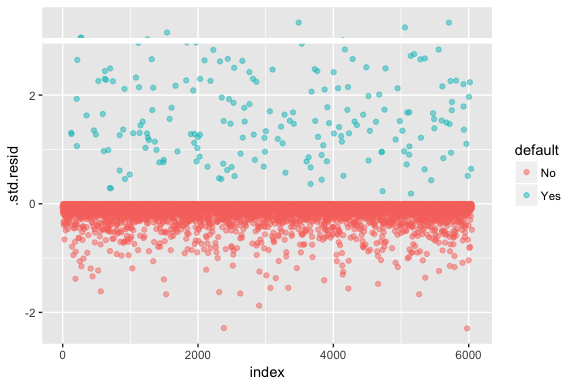

Quali residui standardizzati che superano i 3 rappresentano possibili outlier e possono meritare maggiore attenzione. Possiamo filtrare per questi residui per dare un’occhiata più da vicino. Vediamo che tutte queste osservazioni rappresentano clienti che sono andati in default con budget molto più bassi dei normali inadempienti.

model1_data %>% filter(abs(.std.resid) > 3)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 Yes 1118.7010 -4.664566 0.1752745 3.057432 0.0002841609 0.3857438 0.01508609 3.057867 271## 2 Yes 1119.0972 -4.662320 0.1751742 3.056704 0.0002844621 0.3857448 0.01506820 3.057139 272## 3 Yes 1135.0473 -4.571902 0.1711544 3.027272 0.0002967274 0.3857832 0.01435943 3.027721 1253## 4 Yes 1066.8841 -4.958307 0.1885550 3.151288 0.0002463229 0.3856189 0.01754100 3.151676 1542## 5 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 6 Yes 1143.6805 -4.522962 0.1689933 3.011233 0.0003034789 0.3858039 0.01398491 3.011690 4142## 7 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 8 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709

Similmente alla regressione lineare possiamo anche identificare le osservazioni influenti con i valori della distanza di Cook. Qui identifichiamo i primi 5 valori più grandi.

plot(model1, which = 4, id.n = 5)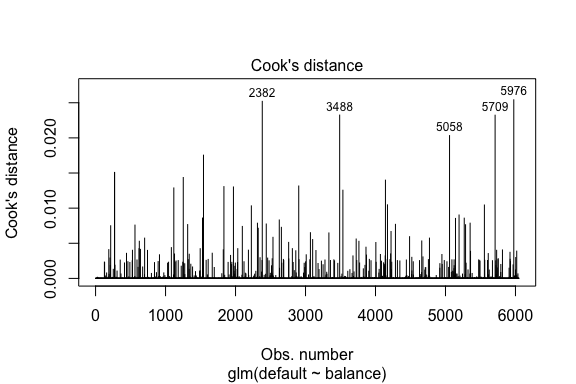

E possiamo indagare ulteriormente anche questi. Qui vediamo che i primi cinque punti influenti includono:

• questi clienti che sono andati in default con saldi molto bassi e
• due clienti che non sono andati in default, ma avevano saldi superiori a $2.000

Questo significa che se dovessimo rimuovere queste osservazioni (non consigliato), la forma, la posizione e l’intervallo di confidenza della nostra curva a S di regressione logistica probabilmente si sposterebbe.

model1_data %>% top_n(5, .cooksd)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 No 2388.1740 2.531843 0.2413764 -2.284011 0.0039757771 0.3866249 0.02520100 -2.288565 2382## 2 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 3 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 4 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709## 5 No 2391.0077 2.547907 0.2421522 -2.290521 0.0039468742 0.3866185 0.02542145 -2.295054 5976

Validazione dei valori previsti

Tasso di classificazione

Quando si sviluppano modelli per la predizione, la metrica più critica riguarda quanto bene fa il modello nel prevedere la variabile target su osservazioni fuori campione. Per prima cosa, abbiamo bisogno di usare i modelli stimati per predire i valori sul nostro set di dati di allenamento (train). Quando si usa predict assicurarsi di includere type = response in modo che la previsione restituisca la probabilità di default.

test.predicted.m1 <- predict(model1, newdata = test, type = "response")test.predicted.m2 <- predict(model2, newdata = test, type = "response")test.predicted.m3 <- predict(model3, newdata = test, type = "response")

Ora possiamo confrontare la variabile obiettivo prevista con i valori osservati per ogni modello e vedere quale si comporta meglio. Possiamo iniziare usando la matrice di confusione, che è una tabella che descrive la performance di classificazione per ogni modello sui dati di test. Ogni quadrante della tabella ha un significato importante. In questo caso i “No” e i “Sì” nelle righe rappresentano se i clienti sono inadempienti o meno. I “FALSO” e “VERO” nelle colonne rappresentano se abbiamo previsto che i clienti fossero inadempienti o meno.

• veri positivi (quadrante in basso a destra): questi sono i casi in cui abbiamo previsto che il cliente sarebbe stato inadempiente e l’ha fatto.
• veri negativi (quadrante in alto a sinistra): Abbiamo previsto che non ci sarebbe stato nessun default e il cliente non lo ha fatto.
• falsi positivi (quadrante in alto a destra): Abbiamo predetto di sì, ma non hanno effettivamente fatto default. (Conosciuto anche come “errore di tipo I”.)
• falsi negativi (quadrante in basso a sinistra): Abbiamo predetto di no, ma hanno fatto default. (Conosciuto anche come “errore di tipo II”.)

I risultati mostrano che model1 e model3 sono molto simili. Il 96% delle osservazioni previste sono veri negativi e circa l’1% sono veri positivi. Entrambi i modelli hanno un errore di tipo II inferiore al 3% in cui il modello predice che il cliente non sarà inadempiente ma in realtà lo è. Ed entrambi i modelli hanno un errore di tipo I inferiore all’1% in cui il modello prevede che il cliente sarà inadempiente ma non lo è mai stato. model2 I risultati sono notevolmente diversi; questo modello predice accuratamente i non inadempienti (un risultato del 97% dei dati che non sono inadempienti) ma non predice mai effettivamente i clienti inadempienti!

list( model1 = table(test$default, test.predicted.m1 > 0.5) %>% prop.table() %>% round(3), model2 = table(test$default, test.predicted.m2 > 0.5) %>% prop.table() %>% round(3), model3 = table(test$default, test.predicted.m3 > 0.5) %>% prop.table() %>% round(3))## $model1## ## FALSE TRUE## No 0.962 0.003## Yes 0.025 0.010## ## $model2## ## FALSE## No 0.965## Yes 0.035## ## $model3## ## FALSE TRUE## No 0.963 0.003## Yes 0.026 0.009

Vogliamo anche capire i tassi di missclassificazione (alias errore) (o potremmo invertire questo per i tassi di precisione). Non vediamo molti miglioramenti tra i modelli 1 e 3 e anche se il modello 2 ha un basso tasso di errore, non dimenticate che non predice mai accuratamente i clienti che sono effettivamente inadempienti.

test %>% mutate(m1.pred = ifelse(test.predicted.m1 > 0.5, "Yes", "No"), m2.pred = ifelse(test.predicted.m2 > 0.5, "Yes", "No"), m3.pred = ifelse(test.predicted.m3 > 0.5, "Yes", "No")) %>% summarise(m1.error = mean(default != m1.pred), m2.error = mean(default != m2.pred), m3.error = mean(default != m3.pred))## # A tibble: 1 × 3## m1.error m2.error m3.error## <dbl> <dbl> <dbl>## 1 0.02782697 0.03491019 0.02807994

Possiamo ottenere ulteriori informazioni guardando i valori grezzi (non le percentuali) nella nostra matrice di confusione. Guardiamo il modello 1 per illustrarlo. Vediamo che c’è un totale di clienti inadempienti. Del totale delle inadempienze, non sono state previste. In alternativa, potremmo dire che solo delle inadempienze sono state previste – questo è noto come la precisione (nota anche come sensibilità) del nostro modello. Quindi, mentre il tasso di errore complessivo è basso, anche il tasso di precisione è basso, il che non è buono!

table(test$default, test.predicted.m1 > 0.5)## ## FALSE TRUE## No 3803 12## Yes 98 40

Con i modelli di classificazione si usano anche i termini sensibilità e specificità quando si caratterizza la performance del modello. Come menzionato sopra, la sensibilità è sinonimo di precisione. Tuttavia, la specificità è la percentuale di non debitori che sono identificati correttamente, qui (la precisione qui è in gran parte guidata dal fatto che il 97% delle osservazioni nei nostri dati sono non debitori). L’importanza tra sensibilità e specificità dipende dal contesto. In questo caso, è probabile che una società di carte di credito sia più interessata alla sensibilità, poiché vuole ridurre il proprio rischio. Pertanto, potrebbero essere più preoccupati di sintonizzare un modello in modo che la loro sensibilità/precisione sia migliorata.

La caratteristica operativa di ricezione (ROC) è una misura visiva delle prestazioni del classificatore. Usando la proporzione di punti di dati positivi che sono considerati correttamente come positivi e la proporzione di punti di dati negativi che sono considerati erroneamente come positivi, generiamo un grafico che mostra il trade off tra il tasso con cui si può prevedere correttamente qualcosa con il tasso di prevedere erroneamente qualcosa. In definitiva, ci interessa l’area sotto la curva ROC, o AUC. Questa metrica varia da 0,50 a 1,00, e i valori superiori a 0,80 indicano che il modello fa un buon lavoro nel discriminare tra le due categorie che comprendono la nostra variabile target. Possiamo confrontare il ROC e l’AUC per i modelli 1 e 2, che mostrano una forte differenza nelle prestazioni. Vogliamo sicuramente che i nostri diagrammi ROC assomiglino di più al modello 1 (a sinistra) piuttosto che al modello 2 (a destra)!

library(ROCR)par(mfrow=c(1, 2))prediction(test.predicted.m1, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()prediction(test.predicted.m2, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()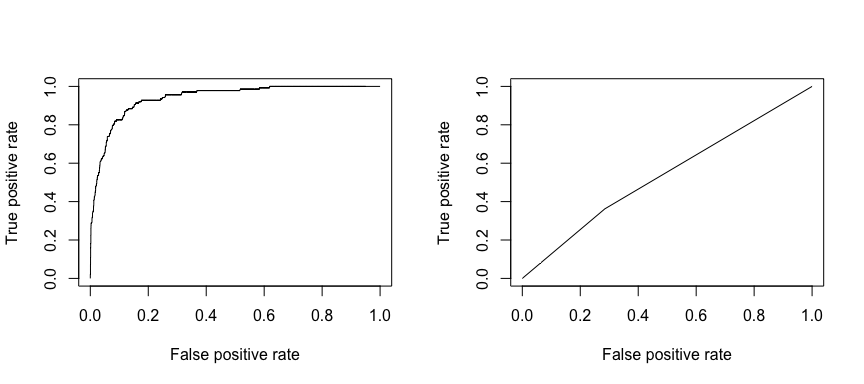

E per calcolare l’AUC numericamente possiamo usare la seguente. Ricordate, l’AUC andrà da 0,50 a 1,00. Quindi, il modello 2 è un modello di classificazione molto povero mentre il modello 1 è un modello di classificazione molto buono.

# model 1 AUCprediction(test.predicted.m1, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.939932# model 2 AUCprediction(test.predicted.m2, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.5386955

Possiamo continuare a “sintonizzare” i nostri modelli per migliorare questi tassi di classificazione. Se riesci a migliorare il tuo AUC e le curve ROC (il che significa che stai migliorando i tassi di accuratezza della classificazione) stai creando un “ascensore”, cioè stai aumentando l’accuratezza della classificazione.

Risorse aggiuntive

Questo ti farà iniziare a lavorare con la regressione logistica. Tieni a mente che c’è molto altro che puoi approfondire, quindi le seguenti risorse ti aiuteranno ad imparare di più:

• Un’introduzione all’apprendimento statistico
• Modellazione predittiva applicata
• Elementi di apprendimento statistico