周波数とは何ですか? 周波数とは、何かが起こる「頻度」です。 音は振動ですから、何かが振動する頻度を表すために周波数を使います。周波数はヘルツ(Hz)で表され、これは単純に「1秒間に何回振動しているか」ということです。 完全な」振動は「サイクル」と呼ばれ、波の1つのピークと谷(すなわち、X軸で表される中央または「0」点より上の最大距離または「振幅」)で測定されます。 (1113>
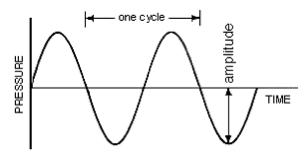
上の図は正弦波で、単一の周波数または振動を最も純粋に表現しています。 波が1サイクルを完了するのにかかる時間が、その波の周波数です(繰り返しますが、「どれくらいの頻度で」振動しているかということです)。 1秒あたりの振動数が多いほど(つまり振動が速いほど)「高い」音域を生み出し、1秒あたりの振動数が少ないほど(つまり振動が遅いほど)「低い」音域を生み出します。
音楽では、周波数、ピッチ、トーンという用語が関連しています。 周波数とは、物理現象を経験的に測定したもので、1秒あたりの(振動の)サイクルとして定義されます。 ピッチは、「高い」または「低い」のように、音の相対的な高さの主観的な知覚です(これについては、Lawerence Zbikowski による Conceptual Modelsand Cross-Domain Mapping を参照してくださいhttp://zbikowski.uchicago.edu/pdfs/ZbikowskiConceptualmodels_1997.pdf)。
周波数が数字 (Hz) で表されるのに対し、ピッチは文字で表されます。 例えば、コンサートの冒頭でオーケストラの「チューニング」を聴いたことがある人は、一人の奏者(通常はオーボエかバイオリン)が440Hzで測定された「A」を演奏します(A440と呼ばれる)。 音程については、A、B、C、D、E、F、Gの文字だけを使う(上げたり下げたりする場合は、さらに記号を使う。) これらの音は8音ごとに繰り返され、オクターブと呼ばれます。音高について話すとき、どのオクターブを指しているのかを区別するために、文字の後に数字が付けられます。 例えば、A440(Hz)は音程的にはA4と呼ばれます。 しかし、ここで混乱してはいけないのは、4はその特定のA(特にピアノの場合)を指しているオクターブを指しているのであって、周波数がたまたま440だっただけで、4が特にそれを指しているわけではないのです。 しかし、なぜA4は440Hzなのか。この質問にはかなり複雑な答えがありますが、結局のところ、恣意的なものです。 簡単に言えば、19世紀にたくさんの人が集まって、そう決めたのです。 (この話題についてもっと知りたいなら、A440やピッチ/チューニングの基準https://en.wikipedia.org/wiki/A440(pitchstandard)で調べてみてください)。
注意すべきは、周波数が絶対であるのに対し、ピッチは相対であるということです(この相対的変化は「チューニング」と呼ばれるものです)。 このように、音高は他の音高との関係(=比率)を記述するために用いられ、その関係を分析することが「音楽理論」の基礎となります。 一般的には、周波数が440Hz(絶対基準)である音程をA4と定義することで合意しています。
すべての音楽理論で非常に重要なことのひとつは、オクターブとは、ある音の周波数を「2倍」または「半分」にしたものであると明確に定義されていることです。 例えば、220Hz、440Hz、880HzはすべてAですが、異なるオクターブで存在します。 それぞれA3、A4、A5となります。 西洋音楽理論では、各オクターブ内に12個の等しい細分化された音高が存在することに一般的に(率直に言って、任意に)合意しています。 では、そのA440に対して、他の音はどのように「調律」されているのだろうか。 さて、長年の実験の結果、次の式で音程(より具体的には、標準的なピアノの第 n キーの周波数 f)の相対的な関係を決定することが決定されました。 この場合の49という数字は任意です(A4は標準的なピアノ鍵盤の49番目のキーです)。コンピュータ音楽では通常、計算にMIDI番号を使用します–例えばA440はMIDIキー番号69です(MIDI標準については別のレッスンで詳しく説明します)。
この式は、西洋クラシック音楽の伝統の中に存在する「調律」の1つの特定のスタイルだけを表しており、一般的にピッチ/周波数/音高の関係について話すときに「世界標準」として使われていることに注意すべきです。このシステムは、各オクターブを12等分するという同じ(ピッチ)比率を維持しながら、オクターブは周波数の正確な2倍またはHalvingとして定義するという重要な「規則」が残されています。 この調律方式を12音平均律と呼び、特に電子音楽機器の標準化においては、世界のほとんどの国で基本的かつ合意された調律方式の基礎となっています。 (すべてのピアノはこの方式で調律され、すべてのMIDIデータはこの一般原則に従っている)
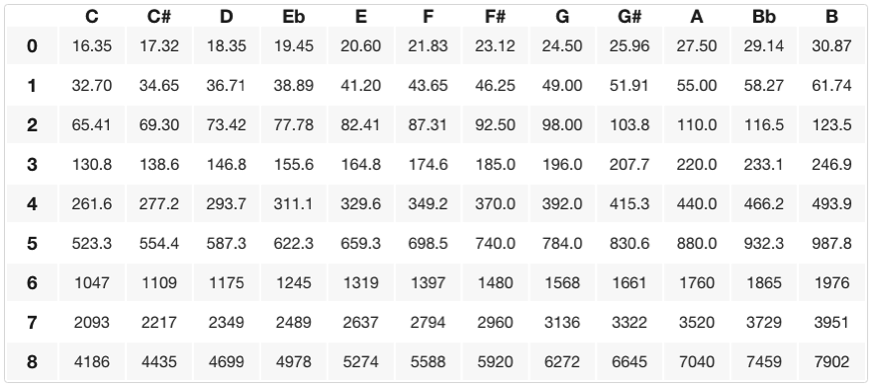
音楽用語では、音程 (または音) を「ステップ」という観点から上昇または下降で表現します。 半音上げるとシャープ(数字やハッシュ記号)、半音下げるとフラット(小文字のbもよく使われます)と呼ばれる♯記号で示されます。 A4から半音上げるには、440Hzに2の12乗をすると、466.2Hzとなり、A#(またはBb)となります。 A#とBbは「エンハーモニック・ノート」と呼ばれ、技術的には同じ周波数ですが、「キー」や音楽の文脈によって異なる「スペル」を持つ可能性があります(これについては別のレッスンで詳しく説明します)。 A4から1つ上の周波数を得るには、440Hzに2の12乗を2回かけると、~493.9HzまたはB4となります。 以下は、すべての特定の周波数とそのピッチ/オクターブの関係の表です(X軸に音名、Y軸にオクターブ番号)
 https://www.seventhstring.com/resources/notefrequencies.html
https://www.seventhstring.com/resources/notefrequencies.html
この「1オクターブあたり12音」の集まりは半音階と呼ばれます。「音階」とは基本周波数またはピッチで始まり/終わり、昇順/下降する音の集合体のことをいいます。 半音階は、任意の音程で始まり、その音程から半音ずつ上がっていく(または下がっていく)ものです。 上のチャートでは、与えられた音(基本音)から始めて、11の半音(隣接する音)を上下に数えることで、半音階の特定の周波数または音/音程を見つけることができます。
気づいたかもしれませんが、上のチャートのいくつかの音は#(シャープ)で「綴られて」おり、他のものはb(フラット)で綴られています。 理論的には、どの音符も、その後ろにこれらの記号をつけることによって、半音または全音を上げたり下げたりすることができます。 しかし、西洋音楽理論の普及と予測可能性から、特定の音は特定の方法で「綴られる」慣習がある。 音符と音程の「エンハーモニック・スペリング」(同じ周波数でありながら異なる音程で表現される音符)については、上の表は、音楽の「調号」の伝統的な慣習に関して最も一般的な音符と音程のスペリングであり、すべての可能性を含んでいるわけではありません。 以下の音は一般的なエンハーモニックスペリングです(スラッシュは音やピッチが同じ周波数であることを示しますが、異なるピッチとして表現されたり「スペル」されたりすることがあります)。
C#/Db D#/Eb F#/Gb G#/Ab A#/Bb
もちろん、理論的にはどんな音でも半音、全音上げることができ、さらに#やb記号でダブルフラットやシャープという上級音楽理論になります。あまり複雑に考えずとも、すべての音階や調は半音と全音の集合体であり、それらの音のスペルは、作曲家が使っている音の関係(つまり比率)を演奏者に伝える手がかりとなるのです。
- ヘルツ(Hz)
- 周波数
- トーン
- ピッチ
- A4(A440)
- オクターブ
- ホールステップ(全音)
- ハーフステップ(半音)