Vergelijkingen van SHM
Bedenk een blok dat aan een veer is bevestigd op een wrijvingsloze tafel (Figuur \(PaginaIndex{3})). De evenwichtsstand (de stand waarin de veer noch uitgerekt noch samengedrukt is) is aangegeven als x = 0 . In de evenwichtsstand is de nettokracht nul.
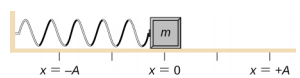
Werkzaamheden worden aan het blok verricht om het uit te trekken tot een positie van x = + A, en vervolgens wordt het uit rust vrijgelaten. De maximale x-positie (A) wordt de amplitude van de beweging genoemd. Het blok begint te oscilleren in de SHM tussen x = + A en x = -A, waarbij A de amplitude van de beweging is en T de periode van de oscillatie. De periode is de tijd voor één oscillatie. In figuur (Pagina-index{4}) is de beweging van het blok te zien terwijl het anderhalve oscillatie doorloopt nadat het is losgelaten.
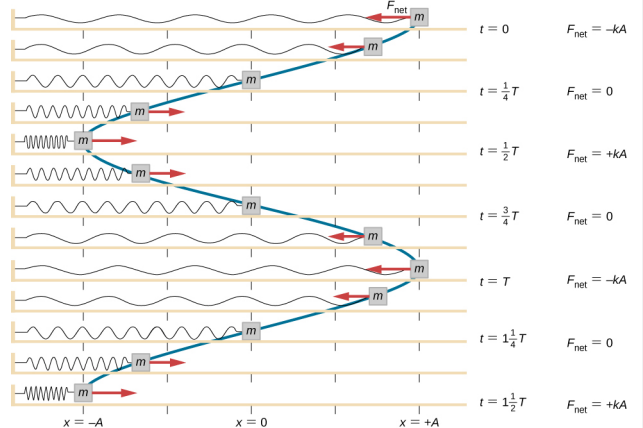
De vergelijking voor de positie als functie van de tijd \(x(t) = Acos( \omega t)\) is goed voor het modelleren van gegevens, waarbij de positie van het blok op het begintijdstip t = 0,00 s op de amplitude A ligt en de beginsnelheid nul is. Vaak is bij het nemen van experimentele gegevens de positie van de massa op het begintijdstip t = 0,00 s niet gelijk aan de amplitude en is de beginsnelheid niet nul. Neem de gegevens van 10 seconden die een leerling in het practicum heeft verzameld, zoals weergegeven in figuur \(\PageIndex{6}\).
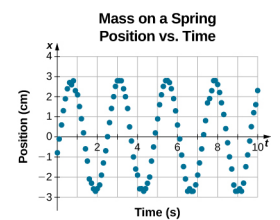
De gegevens in figuur kunnen nog steeds worden gemodelleerd met een periodieke functie, zoals een cosinusfunctie, maar de functie is naar rechts verschoven. Deze verschuiving wordt faseverschuiving genoemd en wordt meestal weergegeven met de Griekse letter phi (fi). De vergelijking van de positie als functie van de tijd voor een blok op een veer wordt
Dit is de algemene vergelijking voor SHM waarbij t de tijd is gemeten in seconden, \(\omega\) de hoekfrequentie met eenheden van inverse seconden, A de amplitude gemeten in meters of centimeters, en \(\phi\) de faseverschuiving gemeten in radialen (figuur \(\PageIndex{7}\)). Omdat sinus- en cosinusfuncties alleen verschillen door een faseverschuiving, zou deze beweging kunnen worden gemodelleerd met de cosinus- of de sinusfunctie.
De snelheid van de massa op een veer, oscillerend in SHM, kan worden gevonden door de afgeleide van de positievergelijking te nemen:
Omdat de sinusfunctie tussen -1 en +1 oscilleert, is de maximumsnelheid de amplitude maal de hoekfrequentie, vmax = A(\omega). De maximumsnelheid treedt op in de evenwichtsstand (x = 0) als de massa naar x = + A beweegt. De maximumsnelheid in negatieve richting treedt op in de evenwichtsstand (x = 0) als de massa naar x = -A beweegt en is gelijk aan -vmax.
De versnelling van de massa op de veer kan worden gevonden door de tijdsafgeleide van de snelheid te nemen: