Dependent vs Independent Events
Een paar posts geleden begon ik te praten over waarschijnlijkheden. Ik wil wat meer tijd aan het onderwerp besteden, omdat het een van die concepten is die het ene moment duidelijk eenvoudig kunnen zijn en het volgende moment ronduit verwarrend.
Wanneer je een waarschijnlijkheidsprobleem benadert waarbij meer dan één gebeurtenis betrokken is, begin dan met je af te vragen of de gebeurtenissen afhankelijk of onafhankelijk zijn, d.w.z. verandert de ene gebeurtenis de waarschijnlijkheid van de andere gebeurtenis? Verandert de eerste gebeurtenis het systeem?
(Het trekken van meerdere kaarten uit een kaartspel zonder vervanging is een klassiek voorbeeld van een afhankelijke gebeurtenis. Als we de eerste kaart trekken, verandert het systeem van 52 mogelijke opties in 51 voordat de tweede gebeurtenis plaatsvindt.)
In het echte leven hebben mensen de neiging om afhankelijkheid voortdurend te verwarren. Bijvoorbeeld, je gooit een munt op. Hij valt 10 keer achter elkaar op kop. Je weet zeker dat de volgende keer munt zal vallen… toch?
Wat is de kans dat de volgende munt weer kop is?
Het is nog steeds 1/2. Het opgooien van een munt is een onafhankelijke gebeurtenis. Met andere woorden, de uitkomst van de volgende worp wordt niet beïnvloed door wat er eerder is gebeurd. Het is alsof het de eerste keer is dat je de munt opgooit. De waarschijnlijkheid is onveranderd.
Waarom “voelt” het dan alsof het munt moet zijn?
We hebben de neiging om over de gebeurtenissen samen na te denken, in plaats van afzonderlijk. Hoewel de kans om kop te gooien bij elke worp gelijk blijft, is de gecombineerde kans om 11 keer achter elkaar kop te gooien klein.
Laten we het eens uitrekenen.
We hebben in de vorige kansrekening geleerd dat wanneer we meerdere gebeurtenissen aan elkaar rijgen en willen dat ze allemaal voorkomen (het “en”-scenario), we hun kansen met elkaar moeten vermenigvuldigen.
Sinds elke muntworp een kans op kop heeft die gelijk is aan 1/2, hoef ik alleen maar elf keer 1/2 met elkaar te vermenigvuldigen.
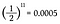
Dat is een kans van 0,05% om elf keer achter elkaar kop te gooien! Maar voordat u opgelucht ademhaalt en zegt: “Zie je wel, ik wist het!”, berekenen we eerst de kans op een munt bij de elfde worp.
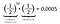
Ja, dat is juist. Het is even waarschijnlijk om tien keer kop te gooien gevolgd door een staart als om elf keer achter elkaar kop te gooien. In feite, omdat de individuele kans om kop te gooien gelijk is aan de kans om munt te gooien, zal elke opstelling van 11 munttoppen resulteren in dezelfde waarschijnlijkheid van 0,0005. Elke opstelling is even waarschijnlijk.
Dus… waarom “voelt” het onwaarschijnlijk om tien keer achter elkaar kop te gooien?
De veel voorkomende misvatting wordt niet veroorzaakt door kansberekening, maar door een verkeerd begrip van combinatoriek en permutaties.
Tot nu toe hebben we vastgesteld dat:
- De kans om kop of munt te gooien is bij elke afzonderlijke worp even waarschijnlijk: P(H) = P(T) = 1/2.
- Elke unieke rangschikking (permutatie) van mogelijke muntopgooiingen is even waarschijnlijk.
Dus wat geeft het?
Uitleg van de steekproefruimte
De steekproefruimte is eenvoudigweg een lijst van alle mogelijke uitkomstschikkingen (permutaties). Omdat de steekproefruimte voor 11 opeenvolgende muntopgooiingen nogal groot is, laten we in plaats daarvan een eenvoudiger geval onderzoeken.
De steekproefruimte voor vier muntopgooiingen is:

Inuïtief zouden we kunnen denken: het is waarschijnlijker om 2 keer kop en 2 keer munt te gooien dan allemaal kop of allemaal munt.
En dit is waar. Laten we eens rekenen.
We weten dat elk van de zestien permutaties even waarschijnlijk is omdat P(H) = P(T) = 1/2. Dus elke permutatie heeft een gelijke kans:

Noot: Omdat de steekproefruimte alle mogelijke uitkomsten weergeeft, is de som van alle kansen altijd gelijk aan 1 (Bijv. 0,0625 – 16 = 1).
Kijkend naar onze steekproefruimte, hoeveel verschillende muntopgooi permutaties resulteren in elke combinatie van 2 kop en 2 munt?

Merk op dat 6 van de 16 mogelijke uitkomsten resulteren in een combinatie van twee koppen en twee staarten. Omdat elk van deze zes permutaties aan onze criteria voldoet, wordt dit beschouwd als een “of”-scenario – dus tel je de kansen bij elkaar op (of vermenigvuldig je ze gewoon met 6 omdat ze allemaal hetzelfde zijn).
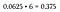
Dat is een kans van 37,5% om een combinatie van 2 koppen en 2 staarten te gooien, wat veel groter is dan de kans om alle koppen of alle staarten te gooien (die blijft 6.
Daarom weten we intuïtief dat het waarschijnlijker is om een gelijk aantal koppen en staarten om te gooien, dan om alles van één soort om te gooien, terwijl we toch het feit behouden dat de gebeurtenissen onafhankelijk zijn met evenveel kans op individuele tosses en permutaties.
Permutaties & Combinaties
Veel van het succesvol berekenen van kansen is het grondig begrijpen van permutaties en combinaties. Dus dat is waar we nu naar toe gaan!