Let’s investigate what happens when negative values appear under the radical symbol (as the radicand) for cube roots and square roots.
W niektórych sytuacjach, liczby ujemne pod symbolem radykalnym są OK. Na przykład, 
nie jest problemem, ponieważ (-2) – (-2) – (-2) = -8, co czyni odpowiedź -2. W cube root problemy, jest możliwe, aby pomnożyć ujemną wartość razy siebie trzy razy i uzyskać negatywną odpowiedź.
Trudności, jednak rozwijać, gdy patrzymy na problem, taki jak 
. Ten problem pierwiastka kwadratowego jest prośbą o liczbę pomnożoną przez siebie, która da produkt (odpowiedź) -16. Po prostu nie ma sposobu, aby pomnożyć liczbę razy siebie i uzyskać wynik ujemny. Rozważmy: (4) – (4) = 16 oraz (-4) – (-4) = 16.
|
CUBE ROOTS:
 |
BUT
|
SQUARE ROOTS:
 |
|
Tak, (-2) x (-2) x (-2) = -8.
No problem. |
Nie! (4) x (4) ≠ -16. |
Winne są pierwiastki kwadratowe! Trudności pojawiają się, gdy napotykamy wartość ujemną pod pierwiastkiem kwadratowym. Nie jest możliwe, aby podnieść wartość do kwadratu (pomnożyć ją razy siebie) i otrzymać wartość ujemną. Co więc robimy?
 |
Pierwiastek kwadratowy liczby ujemnej nie istnieje wśród zbioru liczb rzeczywistych.
|
Gdy po raz pierwszy pojawiły się problemy z ujemnymi pod pierwiastkiem kwadratowym, matematycy sądzili, że rozwiązanie nie istnieje. Widzieli równania takie jak x2 + 1 = 0, i zastanawiali się, co naprawdę oznacza rozwiązanie 
.
W dążeniu do rozwiązania tego problemu, matematycy „stworzyli” nową liczbę, i, która została określona jako „liczba urojona”, ponieważ nie była w zbiorze „liczb rzeczywistych”. Ta nowa liczba była postrzegana z dużym sceptycyzmem. Liczba urojona po raz pierwszy pojawiła się w druku w roku 1545.
 |
Liczba urojona „i” jest pierwiastkiem kwadratowym z ujemnej jedynki. |
Liczba urojona ma tę unikalną własność, że po podniesieniu do kwadratu jej wynik jest ujemny.
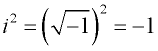
Rozważmy: 
Proces upraszczania rodnika zawierającego czynnik ujemny jest taki sam jak normalne upraszczanie rodnika. Jedyna różnica polega na tym, że 
zostanie zastąpione przez „i „.
Jak badania z liczbami urojonymi kontynuowano, odkryto, że faktycznie wypełniają one lukę w matematyce i służą użytecznemu celowi. Liczby urojone są niezbędne do badania nauk takich jak elektryczność, mechanika kwantowa, analiza drgań i kartografia.
Gdy urojone i zostało połączone ze zbiorem liczb rzeczywistych, powstał wszechogarniający zbiór liczb zespolonych.
.
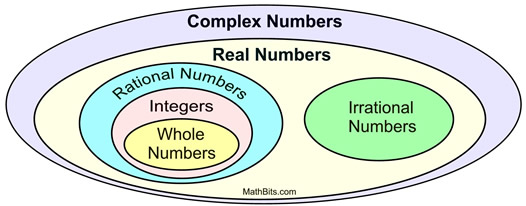