Să investigăm ce se întâmplă când apar valori negative sub simbolul radicalului (ca radicand) pentru rădăcini cubice și rădăcini pătrate.
În unele situații, numerele negative sub un simbol radical sunt OK. De exemplu, 
nu este o problemă, deoarece (-2) – (-2) – (-2) – (-2) = -8, ceea ce face ca răspunsul să fie -2. În problemele de rădăcini cubice, este posibil să înmulțim o valoare negativă cu ea însăși de trei ori și să obținem un răspuns negativ.
Dificultățile apar, totuși, atunci când analizăm o problemă precum 
. Această problemă de rădăcină pătrată cere un număr înmulțit cu el însuși care va da un produs (răspuns) de -16. Pur și simplu nu există nicio modalitate de a înmulți un număr înmulțit cu el însuși și de a obține un rezultat negativ. Luați în considerare: (4) – (4) = 16 și (-4) – (-4) = 16.
|
Rădăcini cubice:
 |
Dar
|
Rădăcini pătrate:
 |
|
Da, (-2) x (-2) x (-2) x (-2) = -8.
Nici o problemă. |
Nici o problemă! (4) x (4) ≠ -16. |
Rădăcinile pătrate sunt vinovate! Dificultățile apar atunci când se întâlnește o valoare negativă sub o rădăcină pătrată. Nu este posibil să ridicăm la pătrat o valoare (să o înmulțim cu ea însăși) și să ajungem la o valoare negativă. Așadar, ce trebuie să facem?
 |
Rădăcina pătrată a unui număr negativ nu există în ansamblul numerelor reale.
|
Când au apărut pentru prima dată problemele cu valori negative sub o rădăcină pătrată, matematicienii au crezut că nu există o soluție. Ei au văzut ecuații precum x2 + 1 = 0 și s-au întrebat ce înseamnă cu adevărat soluția 
.
Într-un efort de a rezolva această problemă, matematicienii au „creat” un nou număr, i, care a fost denumit „număr imaginar”, deoarece nu se afla în setul „numerelor reale”. Acest nou număr a fost privit cu mult scepticism. Numărul imaginar a apărut pentru prima dată tipărit în anul 1545.
 |
Numărul imaginar „i” este rădăcina pătrată a lui unu negativ. |
Un număr imaginar posedă proprietatea unică că, atunci când este ridicat la pătrat, rezultatul este negativ.
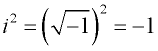
Considerați: 
Procesul de simplificare a unui radical care conține un factor negativ este același cu cel al simplificării normale a radicalilor. Singura diferență este că 
va fi înlocuit cu un „i „.
Pe măsură ce cercetările cu numerele imaginare au continuat, s-a descoperit că acestea umpleau de fapt o lacună în matematică și aveau un scop util. Numerele imaginare sunt esențiale pentru studiul unor științe precum electricitatea, mecanica cuantică, analiza vibrațiilor și cartografia.
Când i imaginar a fost combinat cu setul de numere reale, s-a format setul atotcuprinzător al numerelor complexe.
.
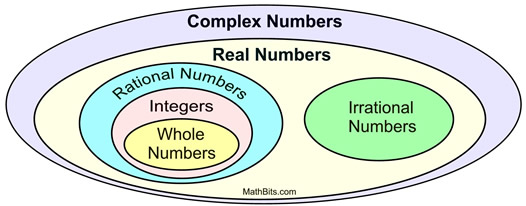