Avhängiga respektive oberoende händelser
För några inlägg sedan började jag tala om sannolikheter. Jag vill ägna lite mer tid åt ämnet eftersom det är ett av de begrepp som kan vara uppenbart enkelt i ena stunden och direkt förvirrande i nästa.
När du närmar dig ett sannolikhetsproblem som inbegriper mer än en händelse börjar du med att fråga dig själv om händelserna är beroende eller oberoende, dvs. ändrar den ena händelsen sannolikheten för den andra händelsen? Ändrar den första händelsen systemet?
(Att dra flera kort från en kortlek utan ersättning är ett klassiskt exempel på en beroende händelse. När vi drar det första kortet ändras systemet från 52 möjliga alternativ till 51 innan den andra händelsen inträffar.)
I det verkliga livet har människor en tendens att förväxla beroende hela tiden. Du slår till exempel ett rättvist mynt. Det landar på huvudet tio gånger i rad. Du är säker på att nästa kast måste bli krona…eller hur?
Hur stor är chansen att nästa mynt blir krona igen?
Det är fortfarande 1/2. Att slå ett mynt är en oberoende händelse. Med andra ord påverkas resultatet av nästa kast inte av vad som har hänt tidigare. Det är som om det vore första gången du vänder myntet. Sannolikheten är oförändrad.
Varför ”känns” det som om det borde bli klave då?
Vi tenderar att tänka på händelserna tillsammans, i stället för var för sig. Även om sannolikheten för att kasta krona förblir densamma för varje kast är den sammanlagda chansen att kasta 11 kronor i rad liten.
Låt oss räkna ut den.
Vi lärde oss i den föregående sannolikhetslektionen att när vi kopplar ihop flera händelser och vill att alla ska inträffa (”och”-scenariot) måste vi multiplicera deras sannolikheter med varandra.
Då varje myntkastning har en sannolikhet för krona lika med 1/2 behöver jag helt enkelt multiplicera ihop 1/2 elva gånger.
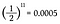
Det är en chans på 0,05 procent att slå elva kronor i rad! Men innan du andas ut en lättnadens suck och säger: ”Se, jag visste det!”, låt oss beräkna chansen att få en svans istället vid det elfte kastet.
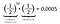
Ja, det är riktigt. Det är lika troligt att slå tio huvuden följt av en svans som att slå elva huvuden i rad. Faktum är att eftersom den individuella sannolikheten för att slå huvudet är densamma som sannolikheten för att slå klave, kommer varje arrangemang av 11 myntkast att resultera i samma sannolikhet på 0,0005. Varje arrangemang är lika sannolikt.
Så… varför ”KÄNNS” det osannolikt att slå tio kronor i rad?
Den vanliga missuppfattningen orsakas inte av sannolikhet, utan av ett missförstånd av kombinatorik och permutationer.
Sedan tidigare har vi fastställt att:
- Sannolikheten för att slå krona eller klave är lika stor vid varje enskilt kast: P(H) = P(T) = 1/2.
- Varje unikt arrangemang (permutation) av möjliga myntkast är lika troligt.
Vad händer då?
Förståelse av samplingsutrymme
Samplingsutrymmet är helt enkelt en förteckning över alla möjliga arrangemang (permutationer) av utfall. Eftersom samplingsutrymmet för 11 på varandra följande myntkastningar är ganska stort, ska vi i stället undersöka ett enklare fall.
Sampelutrymmet för fyra myntkast är:

Intuitivt skulle vi kunna tänka oss: Det är mer troligt att få fram 2 kronor och 2 klappar av fyra kast än att få fram alla kronor eller alla klappar.
Och detta är sant. Låt oss räkna.
Vi vet att var och en av de sexton permutationerna är lika sannolika eftersom P(H) = P(T) = 1/2. Så varje permutation har lika stor sannolikhet:

Notera: Eftersom provutrymmet representerar alla möjliga utfall är summan av alla sannolikheter alltid lika med 1 (T.ex. 0,0625 – 16 = 1).
Om vi tittar på vårt provområde, hur många olika permutationer av myntkastning resulterar i en kombination av 2 krona och 2 klave?

Märk att 6 av 16 möjliga utfall resulterar i en kombination av två huvuden och två svansar. Eftersom någon av dessa sex permutationer uppfyller våra kriterier anses detta vara ett ”eller”-scenario – så addera sannolikheterna tillsammans (eller multiplicera helt enkelt med 6 eftersom de alla är lika).
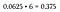
Det är 37,5 % chans att kasta en kombination av två huvuden och två klappar, vilket är mycket större än sannolikheten att kasta alla huvuden eller alla klappar (som fortfarande är 6.25 % vardera eftersom det bara finns en permutation av varje i vårt provområde).
Detta är anledningen till att vi intuitivt vet att det är mer sannolikt att kasta lika många huvuden och klappar, än att kasta alla av ett slag, samtidigt som vi behåller det faktum att händelserna är oberoende med enskilda kast och permutationer som har lika stor sannolikhet att inträffa.
Permutationer&Kombinationer
En stor del av en framgångsrik beräkning av sannolikheter är att förstå permutationer och kombinationer grundligt. Så det är dit vi är på väg nästa gång!