När du ser dig omkring i naturen har du kanske lagt märke till invecklade växter som dessa:


Den här ormbunken består av många små blad som förgrenar sig från ett större.


Den här broccolin består av mindre kottebubesfärer som spiralformar sig runt ett större.
Till en början ser dessa ut som mycket komplexa former – men när du tittar närmare kan du märka att de båda följer ett relativt enkelt mönster: alla enskilda delar av växterna ser exakt likadana ut som hela växten, bara mindre. Samma mönster upprepas om och om igen, i mindre skalor.
I matematiken kallar vi denna egenskap för självlikhet, och former som har den kallas fraktaler. De är några av de vackraste och mest bisarra objekten i hela matematiken.
För att skapa våra egna fraktaler måste vi börja med ett enkelt mönster och sedan upprepa det om och om igen, i mindre skalor.
Ett av de enklaste mönstren kan vara ett linjesegment, med ytterligare två segment som förgrenar sig från ena änden. Om vi upprepar det här mönstret kommer båda dessa blå segment också att ha ytterligare två grenar i sina ändar.
Du kan flytta de blå prickarna för att ändra längden och vinkeln på alla grenar. Öka sedan antalet iterationer med hjälp av reglaget nedan.
Beroende på grenarnas placering kan du skapa helt olika mönster – som ser ut som ormbunken ovan, ett träd eller inbäddade femhörningar. Vad mer kan du hitta?
En annan känd fraktal är Sierpinski-triangeln. I det här fallet börjar vi med en stor, liksidig triangel och skär sedan upprepade gånger ut mindre trianglar ur de återstående delarna.
Lägg märke till hur den slutliga formen består av tre identiska kopior av sig själv, och var och en av dessa består av ännu mindre kopior av hela triangeln! Du kan fortsätta att zooma in i triangeln i all evighet, och mönstren och formerna kommer alltid att fortsätta att upprepas.
Växterna i början av det här kapitlet ser precis ut som fraktaler, men det är helt klart omöjligt att skapa riktiga fraktaler i verkligheten. Om vi fortsätter att upprepa samma mönster om och om igen, mindre och mindre, skulle vi så småningom få celler, molekyler eller atomer som inte längre kan delas upp.
Med hjälp av matematik kan vi dock fundera över de egenskaper som riktiga fraktaler ”skulle” ha – och dessa är mycket överraskande…
Fraktala dimensioner
För det första ska vi fundera över dimensionen hos fraktaler. En linje har dimensionen . När man skalar den med en faktor 2 ökar dess längd med en faktor 21=2. Självklart!
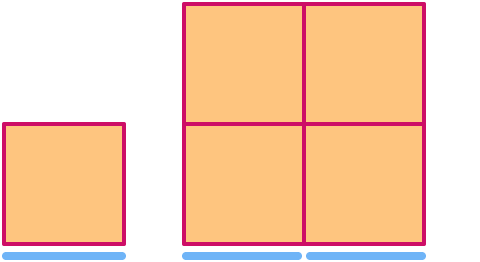
En kvadrat har dimensionen . När den skalas med en faktor 2 ökar dess area med en faktor 22= .
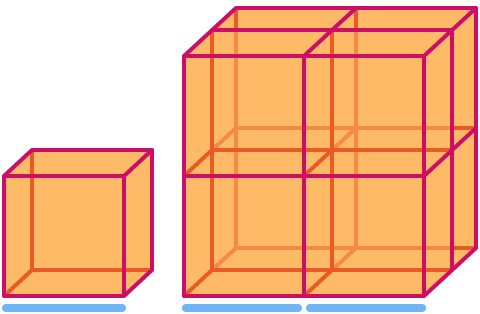
En kub har dimensionen . När den skalas med en faktor 2 ökar dess volym med en faktor 23= . Lägg märke till att den större kuben i bilden består av 8 kopior av den mindre!
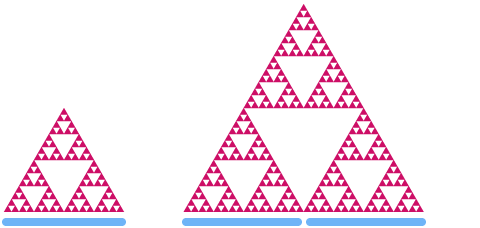
Nu ska vi ta en titt på Sierpinski-triangeln. Om vi skalar den med en faktor 2 kan du se att dess ”area” ökar med en faktor .
Låt oss säga att d är dimensionen för Sierpinski-triangeln. Genom att använda samma mönster som ovan får vi 2d=3. Med andra ord, d = log23log32 ≈ 1,585…
Men vänta … hur kan något ha en dimension som inte är ett heltal? Det verkar omöjligt, men detta är bara en av fraktalernas märkliga egenskaper. Det är faktiskt detta som ger fraktaler deras namn: de har en bråkdimension.
Med varje iteration tar vi bort en del av arean av Sierpinski-triangeln. Om vi kunde göra detta oändligt många gånger skulle det faktiskt inte finnas någon yta kvar: det är därför Sierpinski-triangeln är något mellan en tvådimensionell yta och en endimensionell linje.
Och även om många fraktaler är självliknande är en bättre definition att fraktaler är former som har en icke heltalsdimension.
Kochs snöflinga
Det finns många former i naturen som ser ut som fraktaler. Vi har redan sett några växter i början av det här kapitlet. Andra bra exempel är snöflingor och iskristaller:
För att skapa en egen fraktal snöflinga måste vi än en gång hitta ett enkelt tillvägagångssätt som vi kan tillämpa om och om igen.
Likt Sierpinski-triangeln börjar vi med en enda liksidig triangel. Men i stället för att ta bort mindre trianglar vid varje steg lägger vi till mindre trianglar längs kanten. Sidolängden för varje triangel är 131412 av trianglarna i föregående steg.
Den resulterande formen kallas Kochs snöflinga, uppkallad efter den svenske matematikern Helge von Koch. Lägg än en gång märke till att små kantsektioner av snöflingan ser exakt likadana ut som större sektioner.
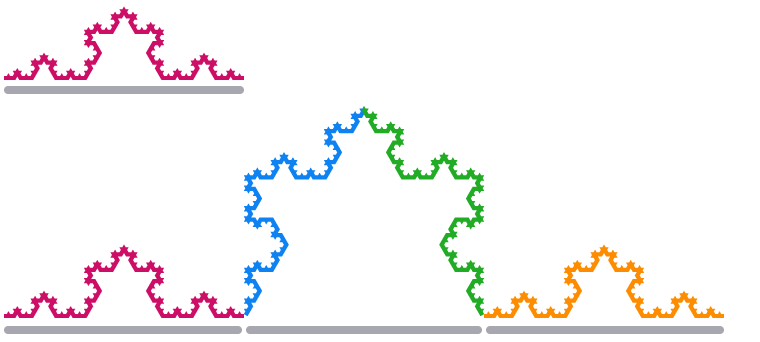
När vi skalar en kantsektion av Kochs snöflinga med en faktor 3, fyrdubblas dess längd.
Genom att använda samma förhållande mellan dimensioner och skalfaktorer som ovan får vi ekvationen 3d=42d=42d=34d=3. Detta innebär att dimensionen för Kochs snöflinga är d=log34≈1,262.
Area
Skapandet av Kochs snöflingor är nästan som en rekursiv sekvens: vi känner till startformen (en triangel), och vi vet hur vi ska ta oss från en term till nästa (genom att lägga till fler trianglar på varje kant):


nya trianglar

nya trianglar

nya trianglar
Efter den första iterationen ökar antalet nya trianglar som läggs till med en faktor av vid varje steg. Samtidigt minskar arean av dessa nya trianglar med en faktor av vid varje steg.
Låt oss säga att den första triangeln har en area på 1. Då är den totala arean av de tre följande trianglarna 3×19=13. De följande stegen bildar alla en geometrisk seriearitmetisk seriekvadratisk serie, med gemensam kvot 499443.
Med hjälp av formeln för summan av oändliga geometriska serier kan vi beräkna att den totala arean av Kochs snöflinga är
A=1+13×11-491+949-14=85=1.6.
Perimeter
Vi kan också försöka beräkna Kochs snöflingas omkrets. Som vi redan har sett tidigare ändras omkretsens längd med en faktor 433414 vid varje steg.
Detta innebär att vi återigen har en geometrisk serie – men i det här fallet konvergerar den intekonvergerar till 0har ingen första term. Detta innebär att Kochs snöflingas omkrets faktiskt är oändligt lång!

Om detta verkar kontraintuitivt är det bara att komma ihåg att vi multiplicerar omkretsen med 43 vid varje steg, och vi gör detta oändligt många gånger.
Det är nästan otänkbart att man kan ha en form med en ändlig yta och samtidigt en oändlig omkrets – men detta är bara en av de många oväntade egenskaperna hos fraktaler.
Kan du komma på några andra sätt att skapa dina egna fraktaler?
”My soul is spiralling on frozen fractals all around…”
Menger Sponge
Fraktaler behöver inte vara ”platta”, som många av exemplen ovan. En av de mest kända fraktalerna som ser tredimensionell ut är Mengersvampen, uppkallad efter matematikern Karl Menger som först beskrev den 1926.
Vi börjar med en solid kub och borrar upprepade gånger mindre och mindre hål i dess sidor. Varje ny iteration av hål har 131214 bredden av den föregående iterationen av hål.
En 3×3×3×3 kub består av 27 mindre kuber, men här har vi tagit bort några av dessa. Mengersvampen består av kopior av sig själv, som är 3 gånger mindre.
Nu kan vi försöka beräkna dimensionen d hos Mengersvampen precis som vi gjorde för Kochs snöflinga ovan. I det här fallet får vi 3d=20, eller d=log320≈2,727.
Om man föreställer sig att man skär ut fler och fler hål, oändligt många gånger, skulle det inte finnas någon egentlig volym kvar. Det är därför kuben är ”inte riktigt” tredimensionell!
Fraktala kustlinjer
En av de viktigaste egenskaperna hos alla fraktaler som vi hittills har sett är att man kan ”zooma in” för evigt och alltid hitta nya mönster. Runt 1920 insåg den brittiske matematikern Lewis Fry Richardson att samma sak gäller för gränsen eller kustlinjen i många länder.
Man börjar med landets grundläggande form och när man zoomar in lägger man till flodmynningar, vikar och flodmynningar, sedan enskilda klippor, klippor, stenar och så vidare:
Det här är ett stort problem när man försöker beräkna längden på gränsen till ett land – hur bestämmer man sig för hur långt man ska zooma in och vilka vinklar och vrår man ska inkludera?
Ett sätt att mäta längden på Storbritanniens kustlinje är till exempel att ta en lång linjal, gå hela vägen runt landets stränder och sedan lägga ihop alla avstånd.
Om linjalen är ${rulers}km lång måste vi använda den ${count} gånger, så vi får en total kustlinje på ${count}. × ${rulers}} = ${count * rulers}km.
Vi kan bara fortsätta, med mindre och mindre linjaler, och varje gång skulle vårt resultat för kustlinjens längd bli lite längre. Precis som Kochs snöflinga tidigare verkar det som om Storbritanniens kustlinje är oändligt lång! Detta kallas ofta för kustlinjeparadoxen.
Några decennier senare snubblade matematikern Benoit Mandelbrot över Richardsons arbete i en kasserad biblioteksbok, när han arbetade på IBM. Han insåg dess betydelse och även hur det hänger samman med nyare forskning om fraktaler och dimensioner.
Den brittiska kusten ”ser visserligen” fraktal ut, men den är inte självliknande, som andra fraktaler vi har sett tidigare. För att ta reda på dess storlek kan vi rita den på ett rutnät och räkna antalet celler som den skär varandra.
Till en början finns det 88 celler som skär varandra. Om vi skalar kustlinjen med en faktor 2 finns det 197 celler som korsar varandra – mer än dubbelt så många!
Kustlinjens storlek har ökat med en faktor 19788. Precis som tidigare innebär detta att kustlinjens dimension är
d=log219788≈1,16
Om vi upprepar detta med större rutnät skulle vi finna att dimensionen på Storbritanniens kustlinje faktiskt är ungefär 1,21. Mandelbrot insåg att denna fraktaldimension också är ett mått på en forms ojämnhet – ett nytt begrepp som han fann viktiga tillämpningar för inom många andra områden av matematik och vetenskap.
Mer fraktaler i natur och teknik
Men även om äkta fraktaler aldrig kan uppträda i naturen finns det många objekt som nästan ser ut som fraktaler. Vi har redan sett växter, snöflingor och kustlinjer, och här är några fler exempel:
Bergskedja i Centralasien
Gangesflodens delta i Indien
Blixtar
Blodkärl i näthinnan
Grand Canyon i USA
Moln
Alla dessa objekt kan verka helt slumpmässiga, men precis som fraktaler finns det ett underliggande mönster som bestämmer hur de bildas. Matematiken kan hjälpa oss att förstå formerna bättre, och fraktaler har tillämpningar inom områden som medicin, biologi, geologi och meteorologi.
Datorgenererad fraktalterräng
Vi kan också använda fraktaler för att skapa realistiska ”kopior” av naturen, till exempel som landskap och texturer som används i videospel eller datorgenererade filmer. Vattnet, bergen och molnen i den här bilden har skapats helt och hållet av en dator med hjälp av fraktaler!
Och vi kan till och med vända den här processen för att komprimera digitala bilder, för att minska deras filstorlek. De första algoritmerna utvecklades av Michael Barnsley och Alan Sloan på 1980-talet, och nya algoritmer forskas fortfarande fram i dag.