Halveringstid

Figur 1. Ett diagram som visar en radioaktiv kärnas sönderfall över tiden. Den tid det tar för källans massa eller aktivitet (antalet sönderfallshändelser per sekund) att sjunka till 50 % är halveringstiden. Halveringstiden i denna bild är 1 år.

Halvlivslängd är den tid som det tar för hälften av det ursprungliga värdet av en viss mängd av ett radioaktivt grundämne att sönderfalla. Dessutom är ett halvliv den tid som det tar för aktiviteten hos en källa att sjunka till hälften av sitt ursprungliga värde. Termodynamikens andra lag, särskilt oordningen, kan användas för att hjälpa till att förstå varför radioaktivt sönderfall sker. Detta påstående säger att entropin i ett slutet system aldrig kan minska, vilket innebär att saker och ting måste falla ytterligare i oordning, inte i ordning. Denna process är känd som ”sönderfall” och den andra lagen hjälper till att klargöra varför materia bryts ner till ett mindre och mindre organiserat tillstånd med tiden. En del av denna process omfattar vissa typer av atomer som bryts ner till nya, olika typer av atomer med en viss mätbar hastighet som kallas radioaktivt sönderfall.

Alla radioaktiva material har instabila atomkärnor i sig. Dessutom finns det också vissa kärnor inom ämnet som redan befinner sig i sitt stabila tillstånd, men förhållandet mellan stabila och instabila kärnor i ett prov kan variera. De stabila kärnorna i provet är oföränderliga (och i ett stabilt energitillstånd), men de instabila kärnorna kommer att genomgå någon form av kärnförfall med tiden för att bli stabila. Detta resulterar i ett utsläpp av någon form av strålning. Eftersom halveringstiden är ett mått på tid är halveringstiden ett värde som bestämmer hur lång tid denna minskning till ett mer stabilt energitillstånd kommer att ta.

Olika ämnen upplever en förlust av sin radioaktivitet snabbare än andra. Vissa radioaktiva grundämnen kan få hälften av sina instabila kärnor att sönderfalla på mindre än en sekund. Krypton-101 har till exempel en halveringstid på ungefär en tio miljondels sekund. Vissa grundämnen har däremot utomordentligt långa halveringstider och tar miljarder år på sig att sönderfalla. Uran-238 har en halveringstid på 4,51 miljarder år. Det innebär att det skulle ta miljarder år för uran-238 att sönderfalla till ett förhållande av hälften uran-238 och hälften torium-234. Uran-235 (en annan naturligt förekommande isotop av uran) har en kortare halveringstid än uran-238, det är bara ~700 miljoner år.

Ekvation

Det finns en ekvation som ofta används för att bestämma hur mycket av ett visst radioaktivt ämne som återstår efter att en viss tid har gått. Detta bestäms utifrån egenskaper som ämnets halveringstid och hur mycket av ämnet det fanns initialt. Ekvationen som används är:

där:

• är mängden substans efter att tiden har gått
• är den ursprungliga mängden substans
• är den tid som har gått
• är substansens halveringstid

Också en liknande ekvation kan användas för att visa hur substansens aktivitet avtar med tiden. När detta uttrycks tar ekvationen formen:

där:

• är ämnets aktivitet efter att tiden har gått
• är ämnets initiala aktivitet
• är den tid som har gått
• är ämnets halveringstid

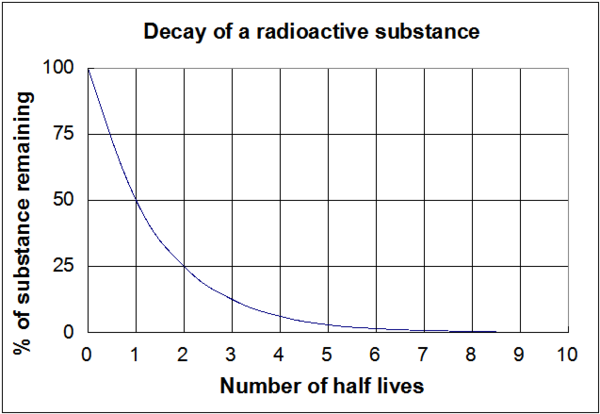
Den graf som visas i figur 1 är en visuell representation av dessa ekvationer ovan. Det är viktigt att notera att oavsett den faktiska längden på halveringstiden (oavsett om den är miljontals år eller några nanosekunder) kommer formen på grafen att vara densamma.

Kunskapen om halveringstider är en del av hur geologer daterar bergarter med radioisotopisk datering.