Eulerova identita je rovnost vyskytující se v matematice, která byla přirovnána k Shakespearovu sonetu a označena jako „nejkrásnější rovnice“. Jedná se o speciální případ základní rovnice komplexní aritmetiky zvané Eulerova formule, kterou zesnulý velký fyzik Richard Feynman ve svých přednáškách nazval „naším klenotem“ a „nejpozoruhodnější formulí v matematice“.
Profesor David Percy z Institutu matematiky a jejích aplikací v rozhovoru pro BBC uvedl, že Eulerova rovnice je „skutečnou klasikou a nic lepšího nemůžete udělat… Je jednoduchá na pohled a přitom neuvěřitelně hluboká, obsahuje pět nejdůležitějších matematických konstant.“
Eulerova identita se zapisuje jednoduše: eiπ + 1 = 0
Pět konstant je:
- Číslo 0.
- Číslo 1.
- Číslo π, iracionální číslo (s nekonečnými číslicemi), které je poměrem obvodu kruhu k jeho průměru. Je to přibližně 3,14159…
- Číslo e, rovněž iracionální číslo. Je to základ přirozeného logaritmu, který vzniká přirozeně studiem složeného úroku a počítáním. Číslo e prostupuje matematikou, objevuje se zdánlivě odnikud v obrovském množství důležitých rovnic. Je přibližně 2,71828….
- Číslo i, definované jako odmocnina ze záporné jedničky: √(-1). Nejzákladnější z imaginárních čísel, které se tak nazývá proto, že ve skutečnosti nelze žádné číslo vynásobit sebou samým, aby vzniklo záporné číslo (a proto záporná čísla nemají reálné odmocniny). V matematice však existuje mnoho situací, kdy je člověk nucen odmocnit záporné číslo. Písmeno i se proto používá jako jakýsi zástupný znak pro označení míst, kde se tak stalo.
Plodný matematik
Leonhard Euler byl matematik švýcarského původu z 18. století, který vytvořil mnoho konceptů, jež jsou nedílnou součástí moderní matematiky. Většinu své kariéry strávil v ruském Petrohradě. Podle údajů Námořní akademie USA (USNA) byl jedním z nejplodnějších matematiků všech dob – publikoval 886 prací a knih. Velká část jeho díla vznikla v posledních dvou desetiletích jeho života, kdy byl zcela slepý. Práce bylo tolik, že petrohradská akademie pokračovala ve vydávání jeho prací posmrtně více než 30 let.
Mezi významné Eulerovy příspěvky patří Eulerova formule a Eulerova věta, přičemž obě mohou v závislosti na kontextu znamenat různé věci. Podle USNA v mechanice existují „Eulerovy úhly (k určení orientace tuhého tělesa), Eulerova věta (že každá rotace má osu), Eulerovy rovnice pro pohyb tekutin a Eulerova-Lagrangeova rovnice (která pochází z variačního počtu).“
Násobení komplexních čísel
Eulerova identita přirozeně vychází z interakcí komplexních čísel, což jsou čísla složená ze dvou částí: reálného čísla a imaginárního čísla; příkladem je 4+3i. Komplexní čísla se objevují v mnoha aplikacích, například ve vlnové mechanice (studium v rámci kvantové mechaniky) a při návrhu obvodů využívajících střídavý proud (běžná praxe v elektrotechnice). Kromě toho mají komplexní čísla (a jejich příbuzná hyperkomplexní čísla) vlastnost, díky níž jsou obzvláště užitečná při studiu počítačové grafiky, robotiky, navigace, letové dynamiky a orbitální mechaniky: jejich násobení způsobuje jejich rotaci. Tato vlastnost nám pomůže pochopit důvody Eulerovy identity.
V níže uvedeném příkladu je pět komplexních čísel vyneseno do komplexní roviny a dohromady tvoří „tvar domu“. Komplexní rovina je podobná číselné přímce s tím rozdílem, že je dvourozměrná. Vodorovný směr představuje reálná čísla a svislá osa imaginární čísla. Každé komplexní číslo ve tvaru domu je vynásobeno komplexním číslem 4+3i a znovu zakresleno (zelená šipka).
Jak je vidět, násobení číslem 4+3i vede k tomu, že se tvar domečku rozšiřuje (zvětšuje se jeho plocha a vzdaluje se od počátku 0+0i o stejnou hodnotu) a otáčí (naklání se o určitý úhel). Abychom ukázali, že právě toto je důsledek násobení číslem 4+3i, je znázorněn také důsledek pětinásobného zvětšení domku a jeho otočení o 36,9 stupně (červená šipka). Vznikne přesně stejný efekt.
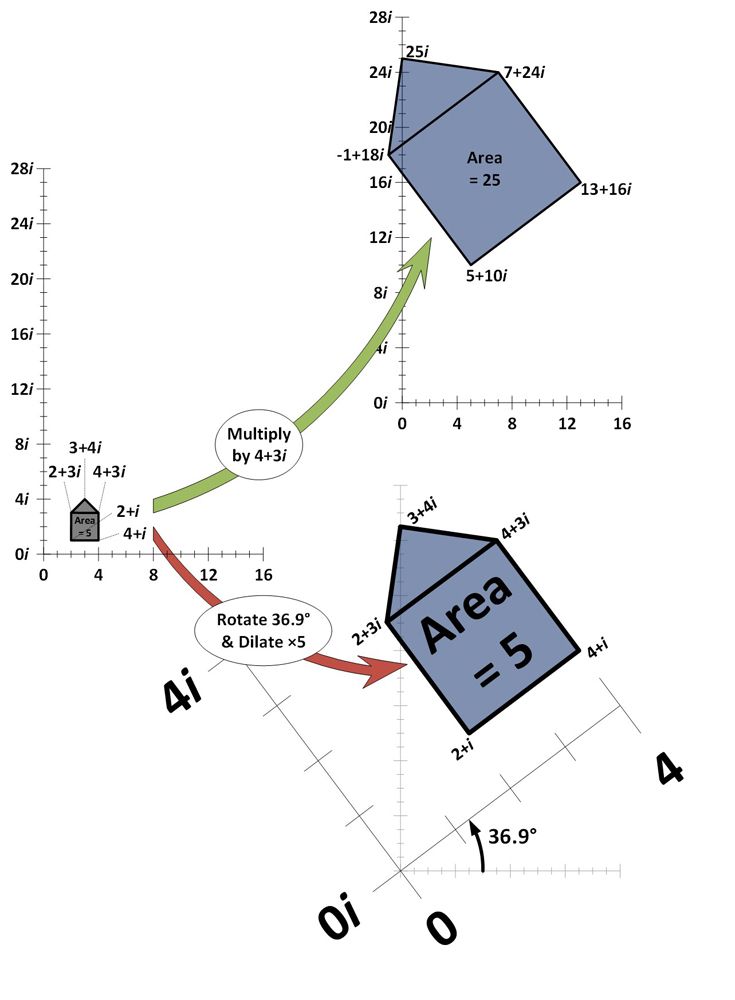
Různé velikosti dilatace a rotace mohou vyvolat efekt násobení libovolným číslem v komplexní rovině.
Polární tvar komplexních čísel
Velikost rotace a dilatace je dána vlastnostmi vlastními číslu 4+3i, které, jak je vidět na obrázku níže, je vzdáleno pět jednotek od počátku (r = 5) a svírá s vodorovnou osou úhel 36,9° (φ = 36,9°). Tyto míry se používají v tzv. polárním tvaru komplexního čísla (reiφ) na rozdíl od normálního obdélníkového tvaru (a+bi).
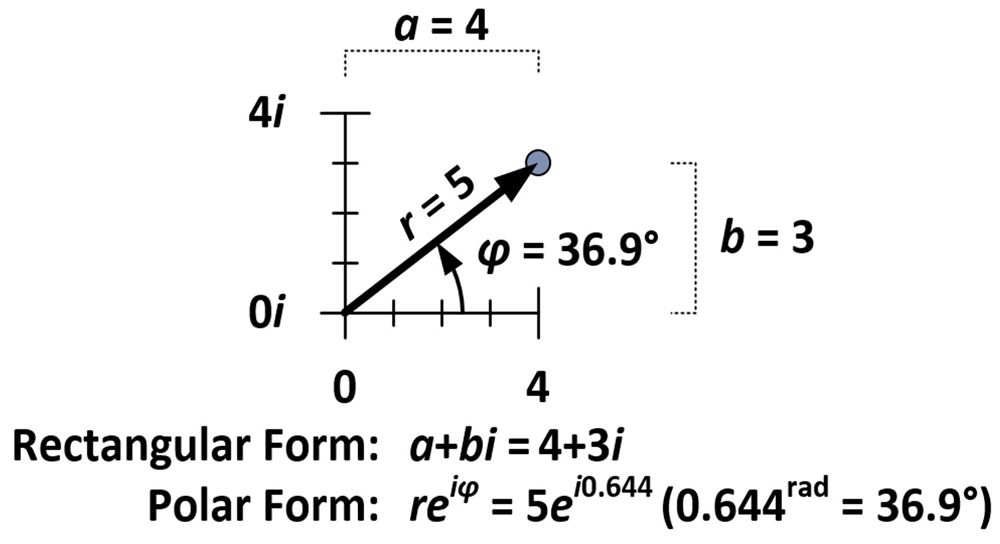
Polární tvar vyžaduje, aby se φ měřilo v radiánech. Jeden radián (1rad) je přibližně 57,3 stupně; je to míra úhlu, který svírá poloměr kružnice s obvodem této kružnice. Míra π radiánů obtáčí polovinu kruhu; míra 2π radiánů obtáčí celý kruh.
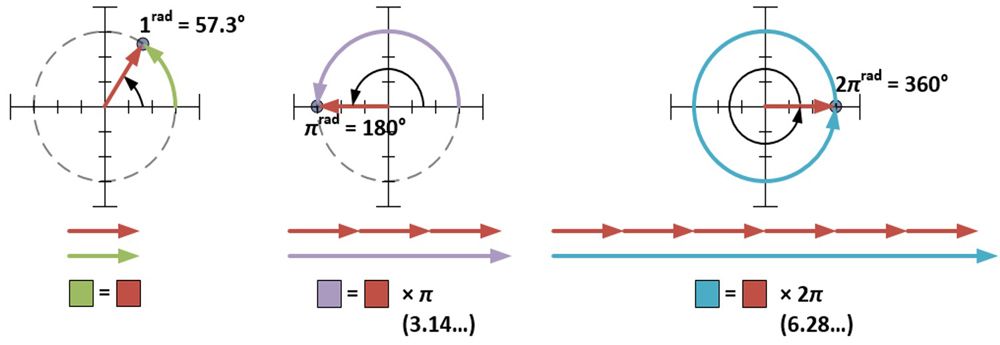
Úhlová míra pro 4+3i je 0,644 radiánu (36,9° = 0,644rad), což znamená, že polární tvar 4+3i je 5ei0,644. Míry pro r a φ lze také určit pro každý z bodů tvaru domu a ještě jeden způsob, jak dosáhnout rozšiřujícího/rotačního efektu násobení 4+3i, je vynásobit každé r pěti a ke každému φ přičíst 36,9° (neboli 0,644rad). Z této ukázky vidíme, že při násobení komplexních čísel se vzdálenosti násobí a úhly sčítají. Je to dáno vlastností vlastní exponentům, kterou lze ukázat algebraicky.
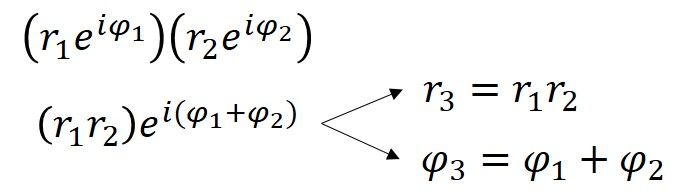
Při zavedeném polárním tvaru komplexních čísel je záležitost Eulerovy identity pouze speciálním případem a+bi pro a = -1 a b = 0. Z toho vyplývá, že pro polární tvar reiφ je to r = 1 a φ = π (protože πrad = 180°).
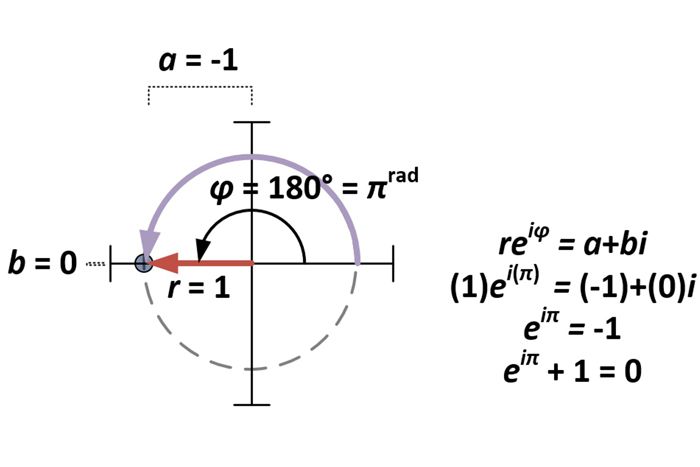
Odvození polárního tvaru
Ačkoli Eulerova identita vyplývá z polárního tvaru komplexního čísla, nelze polární tvar (zejména samočinný výskyt čísla e) odvodit bez kalkulu.
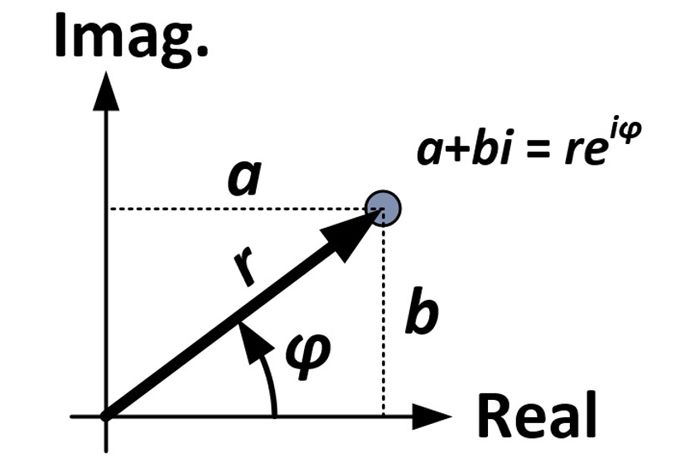
Začneme pravoúhlým tvarem komplexního čísla:
a + bi
Z diagramu a trigonometrie můžeme provést následující substituce:
(r-cosφ) + (r-sinφ)i
Odtud můžeme vynásobit r:
r-(cosφ + i-sinφ)
Někdy se „cosφ + i-sinφ“ nazývá cisφ, což je zkratka pro „kosinus plus imaginární sinus.“
r-cisφ
Ukazuje se, že funkce cisφ je rovna eiφ. To je část, kterou nelze ukázat bez počítání. Dvě derivace jsou uvedeny níže:

Takto se rovnice r-cisφ zapisuje ve standardním polárním tvaru r-eiφ.
.