Tożsamość Eulera jest równością występującą w matematyce, która została porównana do sonetu Szekspira i opisana jako „najpiękniejsze równanie”. Jest to szczególny przypadek fundamentalnego równania w arytmetyce złożonej zwanego Wzorem Eulera, który zmarły wielki fizyk Richard Feynman nazwał w swoich wykładach „naszym klejnotem” i „najbardziej niezwykłym wzorem w matematyce”.
W wywiadzie dla BBC, prof. David Percy z Instytutu Matematyki i jej Zastosowań powiedział, że Tożsamość Eulera była „prawdziwym klasykiem i nie można zrobić nic lepszego niż to … Jest prosta do spojrzenia, a jednak niesamowicie głęboka, obejmuje pięć najważniejszych stałych matematycznych.”
Tożsamość Eulera zapisuje się po prostu jako: eiπ + 1 = 0
Pięć stałych to:
- Liczba 0.
- Liczba 1.
- Liczba π, liczba irracjonalna (z niekończącymi się cyframi), która jest stosunkiem obwodu koła do jego średnicy. W przybliżeniu jest to 3,14159…
- Liczba e, również liczba irracjonalna. Jest podstawą logarytmów naturalnych, które powstają w sposób naturalny poprzez naukę o odsetkach składanych i rachunku. Liczba e przenika matematykę, pojawiając się pozornie znikąd w ogromnej liczbie ważnych równań. Jest to w przybliżeniu 2,71828….
- Liczba i, zdefiniowana jako pierwiastek kwadratowy z ujemnej jedynki: √(-1). Najbardziej podstawowa z liczb urojonych, nazwana tak, ponieważ w rzeczywistości żadna liczba nie może być pomnożona przez siebie, aby otrzymać liczbę ujemną (a zatem liczby ujemne nie mają rzeczywistych pierwiastków kwadratowych). Ale w matematyce istnieje wiele sytuacji, w których jesteśmy zmuszeni do wzięcia pierwiastka kwadratowego z liczby ujemnej. Litera i jest zatem używana jako rodzaj stand-in do oznaczania miejsc, gdzie to zrobiono.
Płodny matematyk
Leonhard Euler był osiemnastowiecznym matematykiem urodzonym w Szwajcarii, który opracował wiele koncepcji, które są integralną częścią współczesnej matematyki. Większość swojej kariery spędził w Petersburgu, w Rosji. Był jednym z najbardziej płodnych matematyków wszechczasów, według U.S. Naval Academy (USNA), z 886 pracami i książkami opublikowanymi. Znaczna część jego dorobku przypadła na ostatnie dwie dekady życia, kiedy był całkowicie niewidomy. Pracy było tak wiele, że Akademia Petersburska kontynuowała pośmiertne publikowanie jego prac przez ponad 30 lat.
Ważny wkład Eulera obejmuje Wzór Eulera i Twierdzenie Eulera, z których oba mogą oznaczać różne rzeczy w zależności od kontekstu. Według USNA, w mechanice istnieją „kąty Eulera (do określenia orientacji ciała sztywnego), twierdzenie Eulera (że każdy obrót ma oś), równania Eulera dla ruchu płynów i równanie Eulera-Lagrange’a (które pochodzi z rachunku wariacji).”
Mnożenie liczb zespolonych
Tożsamość Eulera wynika naturalnie z oddziaływań liczb zespolonych, które są liczbami składającymi się z dwóch części: liczby rzeczywistej i liczby urojonej; przykładem jest 4+3i. Liczby zespolone pojawiają się w wielu zastosowaniach, takich jak mechanika falowa (badanie w ramach mechaniki kwantowej) i projektowanie obwodów, które wykorzystują prąd zmienny (powszechna praktyka w inżynierii elektrycznej). Dodatkowo, liczby zespolone (i ich kuzyni, liczby hiperkompletne) mają własność, która czyni je szczególnie przydatnymi do badania grafiki komputerowej, robotyki, nawigacji, dynamiki lotu i mechaniki orbitalnej: mnożenie ich razem powoduje, że się obracają. Ta właściwość pomoże nam zrozumieć rozumowanie za Euler’s Identity.
W poniższym przykładzie, pięć liczb zespolonych są nakreślone na płaszczyźnie zespolonej i razem tworzą „kształt domu”. Płaszczyzna złożona jest podobna do linii liczbowej, z tym że jest dwuwymiarowa. W kierunku poziomym reprezentuje liczby rzeczywiste, a oś pionowa reprezentuje liczby urojone. Każda liczba złożona w kształcie domu jest pomnożona przez liczbę złożoną 4+3i i ponownie wykreślona (zielona strzałka).
Jak widać, mnożenie przez 4+3i powoduje rozszerzanie się kształtu domu (zwiększenie powierzchni i oddalenie się od początku 0+0i o tę samą wartość) i obracanie (przechylenie o pewien kąt). Aby pokazać, że jest to dokładnie efekt mnożenia przez 4+3i, pokazano również efekt pięciokrotnego powiększenia domu i obrócenia go o 36,9 stopnia (czerwona strzałka). Powstaje dokładnie taki sam efekt.
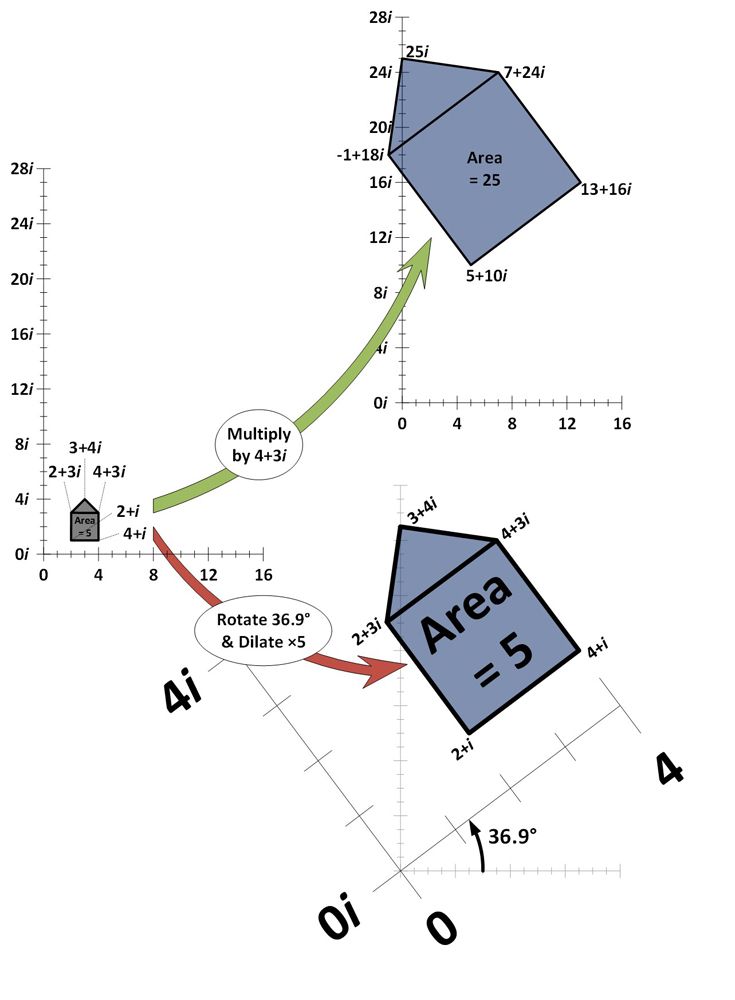
Różne ilości dylatacji i rotacji mogą dać efekt mnożenia przez dowolną liczbę na płaszczyźnie złożonej.
Postać biegunowa liczb zespolonych
Wielkość obrotu i dylatacji jest określona przez własności właściwe liczbie 4+3i, która, jak widać na poniższym rysunku, znajduje się pięć jednostek od początku (r = 5) i tworzy kąt 36,9 stopnia z osią poziomą (φ = 36,9°). Te pomiary są używane w tym, co jest znane jako polarnej postaci liczby złożonej (reiφ), w przeciwieństwie do normalnej postaci prostokątnej (a+bi).
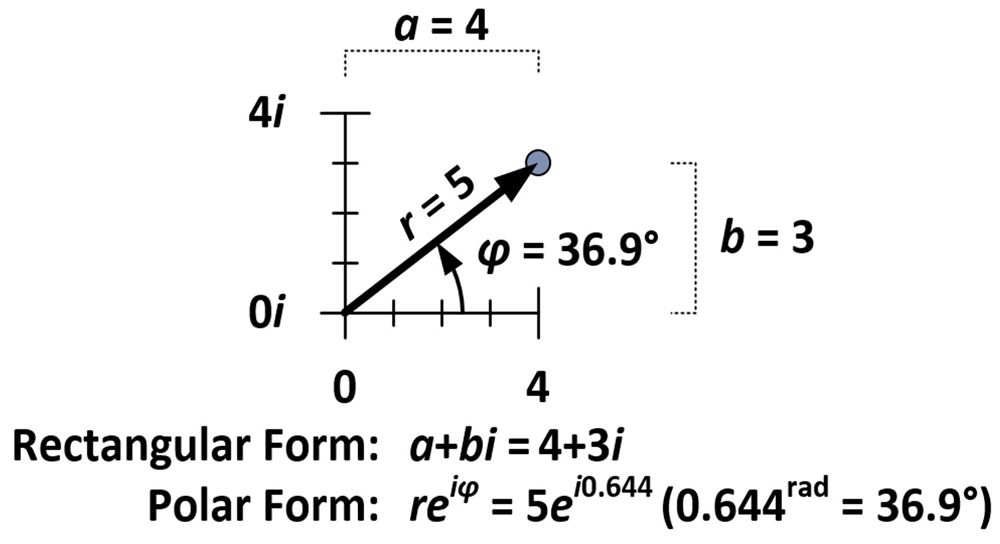
Forma biegunowa wymaga, aby φ była mierzona w radianach. Jeden radian (1rad) to w przybliżeniu 57,3 stopnia; jest to miara kąta utworzonego, gdy promień okręgu jest zawinięty względem obwodu tego okręgu. Miara π radianów owija połowę okręgu; miara 2π radianów owija pełne koło.
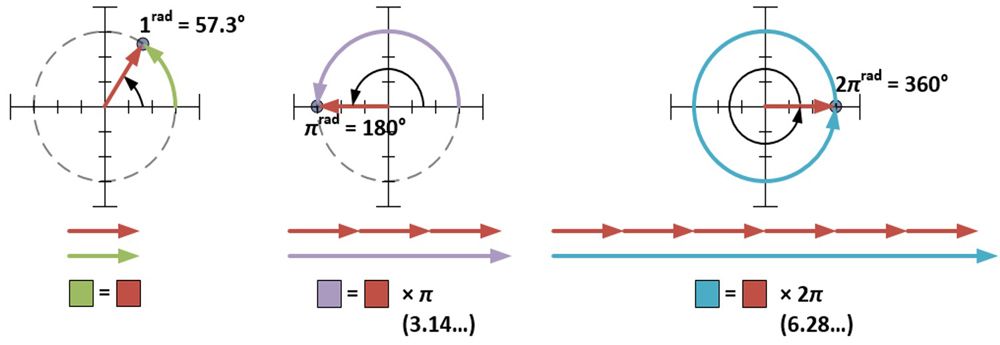
Miara kąta dla 4+3i wynosi 0,644 radiana (36,9° = 0,644rad), co oznacza, że biegunową postacią 4+3i jest 5ei0,644. Miary dla r i φ mogą być również wyznaczone dla każdego z punktów w kształcie domu, a jeszcze innym sposobem uzyskania efektu rozszerzania/obracania przez mnożenie przez 4+3i jest pomnożenie każdego r przez pięć i dodanie 36,9 stopni (lub 0,644rad) do każdego φ. Z tej demonstracji widzimy, że gdy liczby zespolone są mnożone razem, odległości się mnożą i kąty dodają. Wynika to z właściwości nierozerwalnie związanej z wykładnikami, którą można pokazać algebraicznie.
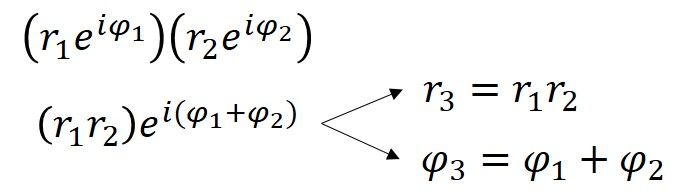
Po ustaleniu postaci biegunowej liczb zespolonych, zagadnienie tożsamości Eulera jest jedynie szczególnym przypadkiem a+bi dla a = -1 i b = 0. W konsekwencji dla formy biegunowej reiφ, to sprawia, że r= 1 i φ = π (ponieważ πrad = 180°).
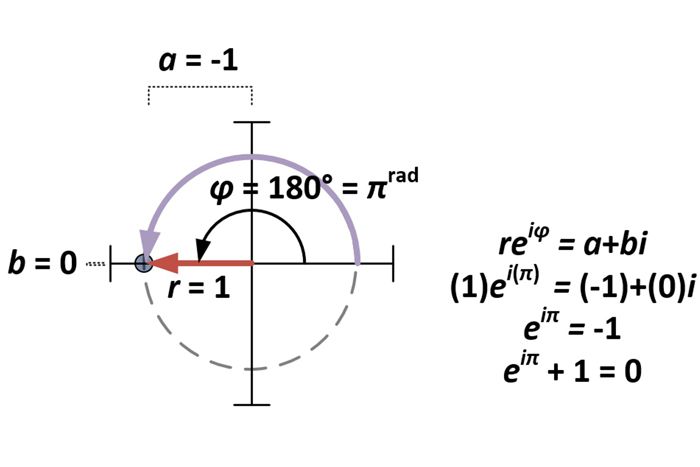
Pochodna postaci biegunowej
Chociaż Tożsamość Eulera wynika z postaci biegunowej liczb zespolonych, to nie da się jej wyprowadzić (w szczególności spontanicznego pojawienia się liczby e) bez rachunku.
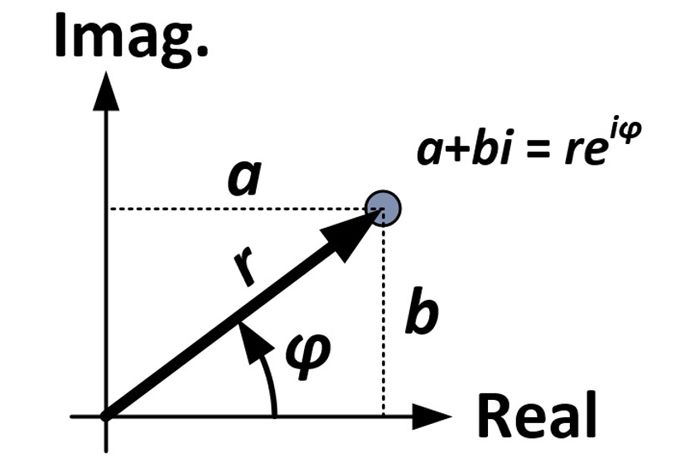
Zaczynamy od prostokątnej postaci liczby zespolonej:
a + bi
Z diagramu i trygonometrii możemy dokonać następujących podstawień:
(r-cosφ) + (r-sinφ)i
Z tego miejsca możemy wyfaktorować r:
r-(cosφ + i-sinφ)
Czasami „cosφ + i-sinφ” jest nazywane cisφ, co jest skrótem od „cosinus plus sinus urojony.”
r-cisφ
Funkcja cisφ okazuje się być równa eiφ. To jest ta część, której nie da się pokazać bez rachunku. Dwie pochodne są pokazane poniżej:

Tak więc, równanie r-cisφ zapisujemy w standardowej postaci biegunowej r-eiφ.
.