Eulerin identiteetti on matematiikassa esiintyvä yhtälö, jota on verrattu Shakespearen sonettiin ja kuvattu ”kauneimmaksi yhtälöksi”. Se on erikoistapaus kompleksisen aritmetiikan perustavanlaatuisesta yhtälöstä nimeltä Eulerin kaava, jota edesmennyt suuri fyysikko Richard Feynman kutsui luennoillaan ”jalokiveksemme” ja ”matematiikan merkittävimmäksi kaavaksi”.
BBC:n haastattelussa matematiikan ja sen sovellusten instituutin professori David Percy sanoi, että Eulerin identiteetti on ”todellinen klassikko, et voi tehdä mitään parempaa … Se on yksinkertainen katsoa ja silti uskomattoman syvällinen, se käsittää viisi tärkeintä matemaattista vakiota”.”
Eulerin identiteetti kirjoitetaan yksinkertaisesti: eiπ + 1 = 0
Viisi vakiota ovat:
- Luku 0.
- Luku 1.
- Luku π, irrationaaliluku (jossa on loputtomia numeroita), joka on ympyrän kehän ja halkaisijan suhde. Se on noin 3,14159…
- Luku e, myös irrationaaliluku. Se on luonnollisten logaritmien perusta, joka syntyy luonnollisesti koronkoron ja laskennan opiskelun kautta. Luku e läpäisee matematiikan, sillä se esiintyy näennäisesti tyhjästä valtavassa määrässä tärkeitä yhtälöitä. Se on noin 2.71828….
- Luku i, joka on määritelty negatiivisen ykkösen neliöjuurena: √(-1). Kuvitteellisista luvuista perustavanlaatuisin, niin kutsuttu, koska todellisuudessa mikään luku ei voi kertoa itsellään negatiivisen luvun saamiseksi (ja siksi negatiivisilla luvuilla ei ole todellisia neliöjuuria). Matematiikassa on kuitenkin monia tilanteita, joissa on pakko ottaa neliöjuuri negatiivisesta luvusta. Siksi i-kirjainta käytetään eräänlaisena sijaiskirjaimena merkitsemään paikkoja, joissa näin on tehty.
Tuottelias matemaatikko
Leonhard Euler oli 1700-luvun sveitsiläissyntyinen matemaatikko, joka kehitti monia käsitteitä, jotka ovat olennainen osa modernia matematiikkaa. Hän vietti suurimman osan urastaan Pietarissa, Venäjällä. Hän oli Yhdysvaltain merivoimien akatemian (USNA) mukaan yksi kaikkien aikojen tuotteliaimmista matemaatikoista 886 julkaistulla artikkelilla ja kirjalla. Suuri osa hänen tuotannostaan syntyi hänen elämänsä kahden viimeisen vuosikymmenen aikana, jolloin hän oli täysin sokea. Työtä oli niin paljon, että Pietarin akatemia jatkoi hänen töidensä julkaisemista postuumisti yli 30 vuoden ajan.
Eulerin tärkeisiin aikaansaannoksiin kuuluvat Eulerin kaava ja Eulerin teoreema, jotka molemmat voivat tarkoittaa eri asioita asiayhteydestä riippuen. USNA:n mukaan mekaniikassa on ”Eulerin kulmat (joilla määritetään jäykän kappaleen suunta), Eulerin teoreema (että jokaisella pyörimisellä on akseli), Eulerin yhtälöt nesteiden liikkeelle ja Euler-Lagrangen yhtälö (joka tulee variaatiolaskennasta).”
Kompleksilukujen kertominen
Eulerin identiteetti juontaa juurensa luonnollisesti kompleksilukujen vuorovaikutuksista, jotka ovat lukuja, jotka koostuvat kahdesta osasta: reaaliluvusta ja imaginääriluvusta; esimerkki on 4+3i. Kompleksiluvut esiintyvät monissa sovelluksissa, kuten aaltomekaniikassa (kvanttimekaniikkaan kuuluva tutkimus) ja vaihtovirtaa käyttävien piirien suunnittelussa (yleinen käytäntö sähkötekniikassa). Lisäksi kompleksiluvuilla (ja niiden sukulaisluvuilla, hyperkompleksiluvuilla) on ominaisuus, joka tekee niistä erityisen käyttökelpoisia tietokonegrafiikan, robotiikan, navigoinnin, lentodynamiikan ja kiertoratamekaniikan tutkimisessa: niiden kertominen keskenään saa ne pyörimään. Tämä ominaisuus auttaa meitä ymmärtämään Eulerin identiteetin taustalla olevia perusteluja.
Alla olevassa esimerkissä viisi kompleksilukua on piirretty kompleksitasolle ja ne muodostavat yhdessä ”talon muodon”. Kompleksitaso on samanlainen kuin lukujono, paitsi että se on kaksiulotteinen. Vaakasuunta edustaa reaalilukuja ja pystyakseli imaginaarilukuja. Jokainen talonmuotoinen kompleksiluku kerrotaan kompleksiluvulla 4+3i ja piirretään uudelleen (vihreä nuoli).
Kuten nähdään, kertominen luvulla 4+3i johtaa siihen, että talomuoto laajenee (pinta-ala kasvaa ja etääntyy origosta 0+0i saman verran) ja kiertyy (kallistuu jonkin kulman verran). Jotta voidaan osoittaa, että juuri tämä on 4+3i:llä kertomisen vaikutus, näytetään myös vaikutus, joka syntyy, kun taloa suurennetaan viisi kertaa ja käännetään 36,9 astetta (punainen nuoli). Saadaan aikaan täsmälleen sama vaikutus.
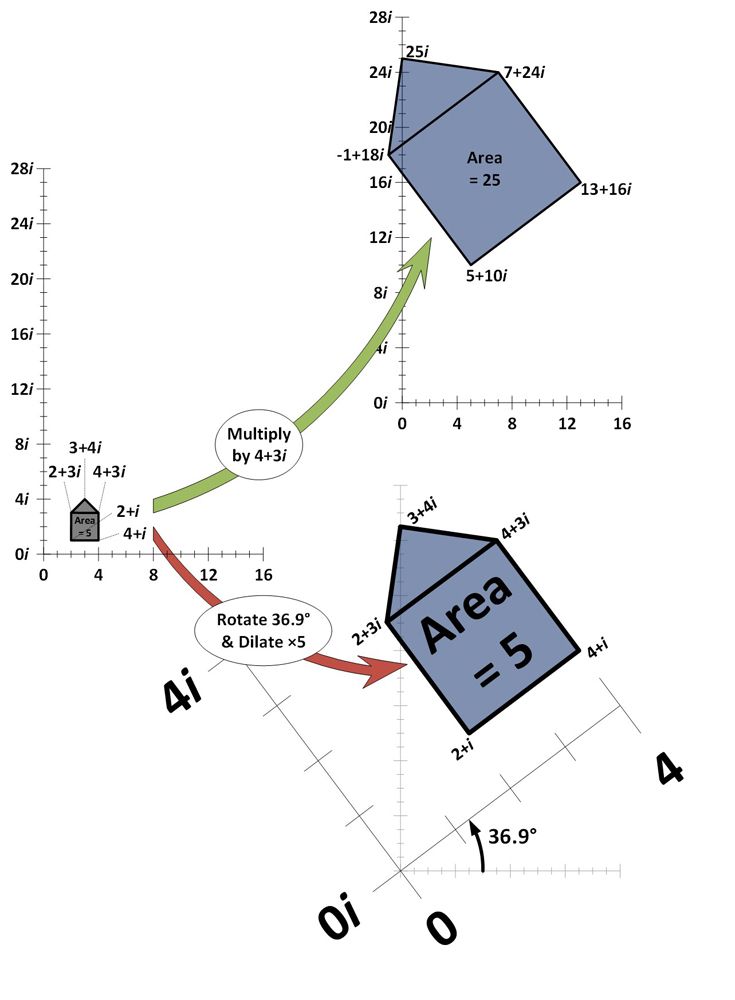
Erilukuisilla dilataatioilla ja rotaatioilla voidaan saada aikaan kompleksitasossa millä tahansa luvulla kertomisen vaikutus.
Kompleksilukujen polaarinen muoto
Kierron ja dilataation määrä määräytyy luvulle 4+3i ominaisten ominaisuuksien perusteella, joka, kuten alla olevasta kuvasta nähdään, on viisi yksikköä origosta (r = 5) ja muodostaa vaaka-akselin kanssa 36,9 asteen kulman (φ = 36,9°). Näitä mittoja käytetään niin sanotussa kompleksiluvun polaarisessa muodossa (reiφ) vastakohtana normaalille suorakulmaiselle muodolle (a+bi).
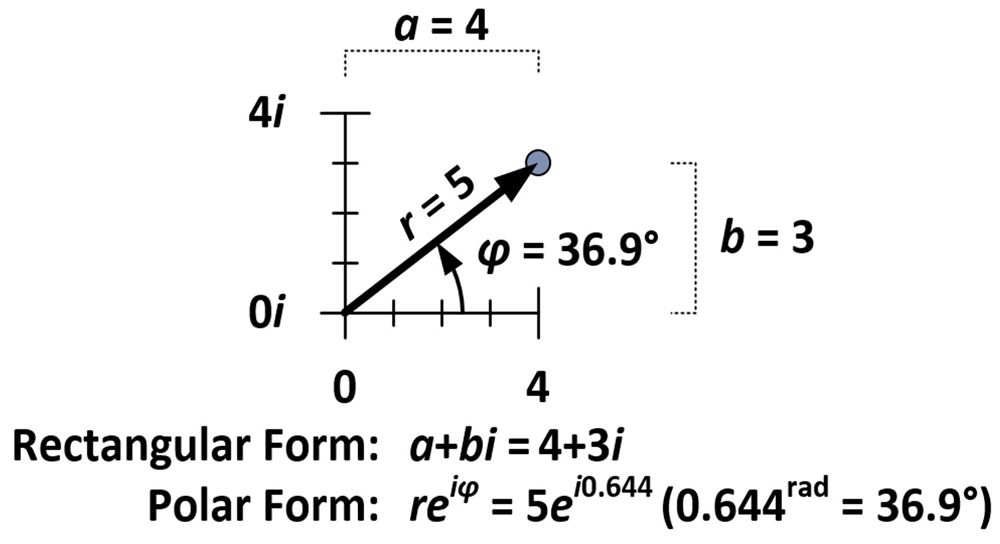
Polaarimuoto edellyttää, että φ mitataan radiaaneina. Yksi radiaani (1rad) on noin 57,3 astetta; se on kulman mitta, joka muodostuu, kun ympyrän säde kiedotaan ympyrän kehää vasten. Mitta π radiaania kiertää ympyrän puoliväliä; mitta 2π radiaania kiertää koko ympyrän.
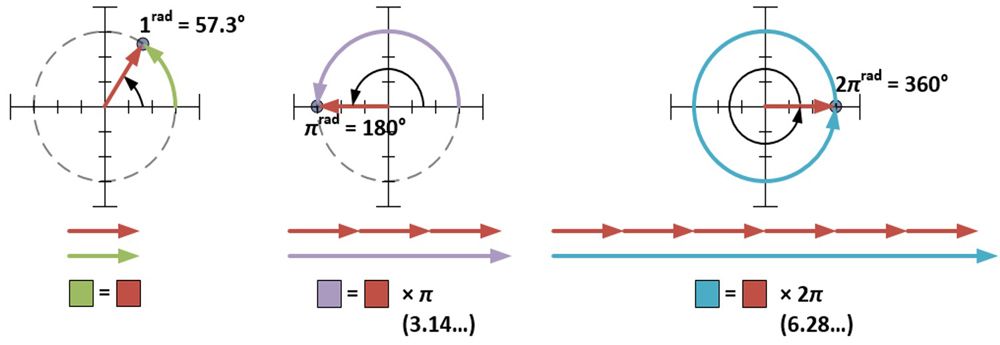
Kulmamitta 4+3i on 0,644 radiaania (36,9° = 0,644rad) eli 4+3i:n polaarimuoto on 5ei0,644. Myös r:n ja φ:n mitat voidaan määrittää kullekin talonmuotoiselle pisteelle, ja toinen tapa saada aikaan 4+3i:llä kertomisen laajentava/pyörittävä vaikutus on kertoa jokainen r viidellä ja lisätä 36,9 astetta (tai 0,644 radia) kuhunkin φ:hen. Tästä havainnosta nähdään, että kun kompleksiluvut kerrotaan keskenään, etäisyydet moninkertaistuvat ja kulmat summautuvat. Tämä johtuu eksponenttien luontaisesta ominaisuudesta, joka voidaan osoittaa algebrallisesti.
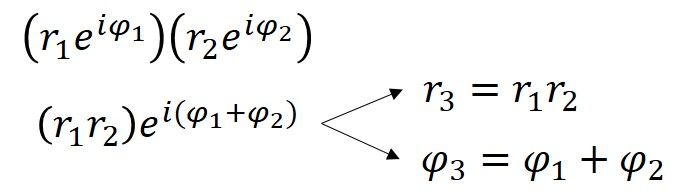
Kompleksilukujen polaarimuodon ollessa selvillä Eulerin identiteetin asia on vain erikoistapaus a+bi, kun a = -1 ja b = 0. Näin ollen polaarimuodolle reiφ tämä tekee r= 1 ja φ = π (koska πrad = 180°).
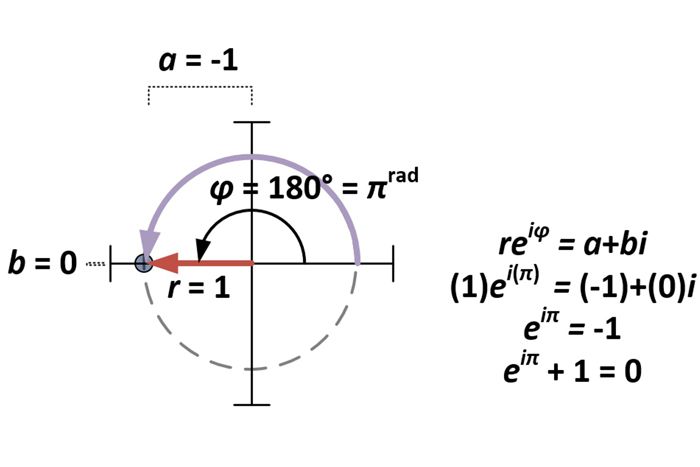
Polaarimuodon johtaminen
Vaikka Eulerin identiteetti seuraa kompleksilukujen polaarimuodosta, polaarimuodon johtaminen (erityisesti luvun e spontaani esiintyminen) on mahdotonta ilman laskutoimitusta.
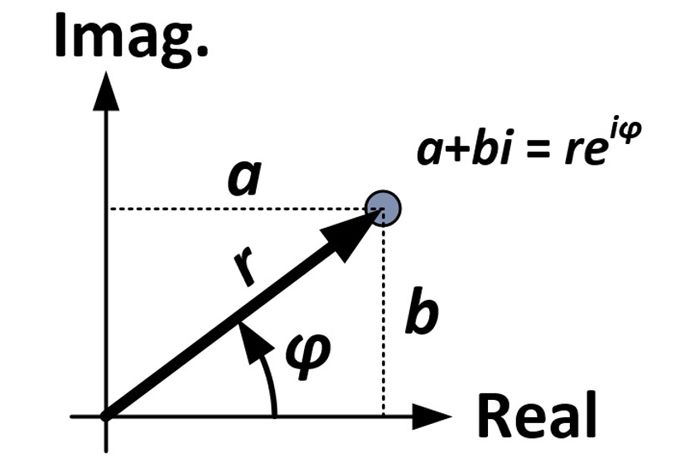
Aloitetaan kompleksiluvun suorakulmaisesta muodosta:
a + bi
Diagrammista ja trigonometriasta voimme tehdä seuraavat korvaukset:
(r-cosφ) + (r-sinφ)i
Tästä voimme kertoa r:
r-(cosφ + i-sinφ)
Joskus ”cosφ + i-sinφ” on nimetty cisφ:ksi, joka on lyhenne sanoista ”kosini plus imaginäärinen sini.”
r-cisφ
Funktio cisφ osoittautuu yhtä suureksi kuin eiφ. Tätä osaa on mahdotonta osoittaa ilman laskutoimitusta. Alla on esitetty kaksi derivaatiota:

Tällöin yhtälö r-cisφ kirjoitetaan tavallisessa polaarisessa muodossa r-eiφ.