L’identité d’Euler est une égalité trouvée en mathématiques qui a été comparée à un sonnet de Shakespeare et décrite comme « la plus belle équation ». C’est un cas particulier d’une équation fondatrice de l’arithmétique complexe appelée formule d’Euler, que le regretté grand physicien Richard Feynman appelait dans ses conférences « notre joyau » et « la formule la plus remarquable des mathématiques. »
Dans une interview accordée à la BBC, le professeur David Percy, de l’Institut des mathématiques et de leurs applications, a déclaré que l’identité d’Euler était « un véritable classique et vous ne pouvez pas faire mieux que cela… Elle est simple à regarder et pourtant incroyablement profonde, elle comprend les cinq constantes mathématiques les plus importantes. »
L’Identité d’Euler s’écrit simplement comme suit : eiπ + 1 = 0
Les cinq constantes sont :
- Le nombre 0,
- Le nombre 1,
- Le nombre π, un nombre irrationnel (avec des chiffres sans fin) qui est le rapport entre la circonférence d’un cercle et son diamètre. Il vaut approximativement 3,14159…
- Le nombre e, également un nombre irrationnel. C’est la base des logarithmes naturels qui naît naturellement de l’étude des intérêts composés et du calcul. Le nombre e est omniprésent en mathématiques, apparaissant apparemment de nulle part dans un grand nombre d’équations importantes. Il est approximativement égal à 2,71828….
- Le nombre i, défini comme la racine carrée du un négatif : √(-1). Le plus fondamental des nombres imaginaires, ainsi appelé parce que, en réalité, aucun nombre ne peut être multiplié par lui-même pour produire un nombre négatif (et, par conséquent, les nombres négatifs n’ont pas de véritables racines carrées). Mais en mathématiques, il existe de nombreuses situations où l’on est obligé de prendre la racine carrée d’un négatif. La lettre i est donc utilisée comme une sorte de doublure pour marquer les endroits où cela a été fait.
Mathématicien prolifique
Leonhard Euler était un mathématicien du 18e siècle, né en Suisse, qui a développé de nombreux concepts qui font partie intégrante des mathématiques modernes. Il a passé la majeure partie de sa carrière à Saint-Pétersbourg, en Russie. Il est l’un des mathématiciens les plus prolifiques de tous les temps, selon l’Académie navale américaine (USNA), avec 886 articles et livres publiés. La plupart de ses travaux ont été réalisés au cours des deux dernières décennies de sa vie, alors qu’il était totalement aveugle. Il y avait tellement de travail que l’Académie de Saint-Pétersbourg a continué à publier ses travaux à titre posthume pendant plus de 30 ans.
Les contributions importantes d’Euler comprennent la formule d’Euler et le théorème d’Euler, qui peuvent tous deux signifier différentes choses selon le contexte. Selon l’USNA, en mécanique, il y a « les angles d’Euler (pour spécifier l’orientation d’un corps rigide), le théorème d’Euler (que toute rotation a un axe), les équations d’Euler pour le mouvement des fluides, et l’équation d’Euler-Lagrange (qui vient du calcul des variations). »
Multiplication des nombres complexes
L’identité d’Euler découle naturellement des interactions des nombres complexes qui sont des nombres composés de deux morceaux : un nombre réel et un nombre imaginaire ; un exemple est 4+3i. Les nombres complexes apparaissent dans une multitude d’applications telles que la mécanique ondulatoire (une étude de la mécanique quantique) et la conception de circuits utilisant du courant alternatif (une pratique courante en électrotechnique). En outre, les nombres complexes (et leurs cousins, les nombres hyper complexes) ont une propriété qui les rend particulièrement utiles pour l’étude de l’infographie, de la robotique, de la navigation, de la dynamique de vol et de la mécanique orbitale : leur multiplication les fait tourner. Cette propriété nous aidera à comprendre le raisonnement derrière l’identité d’Euler.
Dans l’exemple ci-dessous, cinq nombres complexes sont tracés sur le plan complexe et forment ensemble une « forme de maison ». Le plan complexe est similaire à une ligne de nombres, sauf qu’il est bidimensionnel. L’axe horizontal représente les nombres réels et l’axe vertical les nombres imaginaires. Chaque nombre complexe en forme de maison est multiplié par le nombre complexe 4+3i et re-tracé (flèche verte).
Comme on peut le voir, la multiplication par 4+3i entraîne une dilatation (augmentation de la surface et éloignement de l’origine 0+0i de la même quantité) et une rotation (inclinaison d’un certain angle) de la forme de la maison. Pour montrer que c’est précisément l’effet de la multiplication par 4+3i, l’effet d’un zoom sur la maison cinq fois et d’une rotation de 36,9 degrés est également montré (flèche rouge). On obtient exactement le même effet.
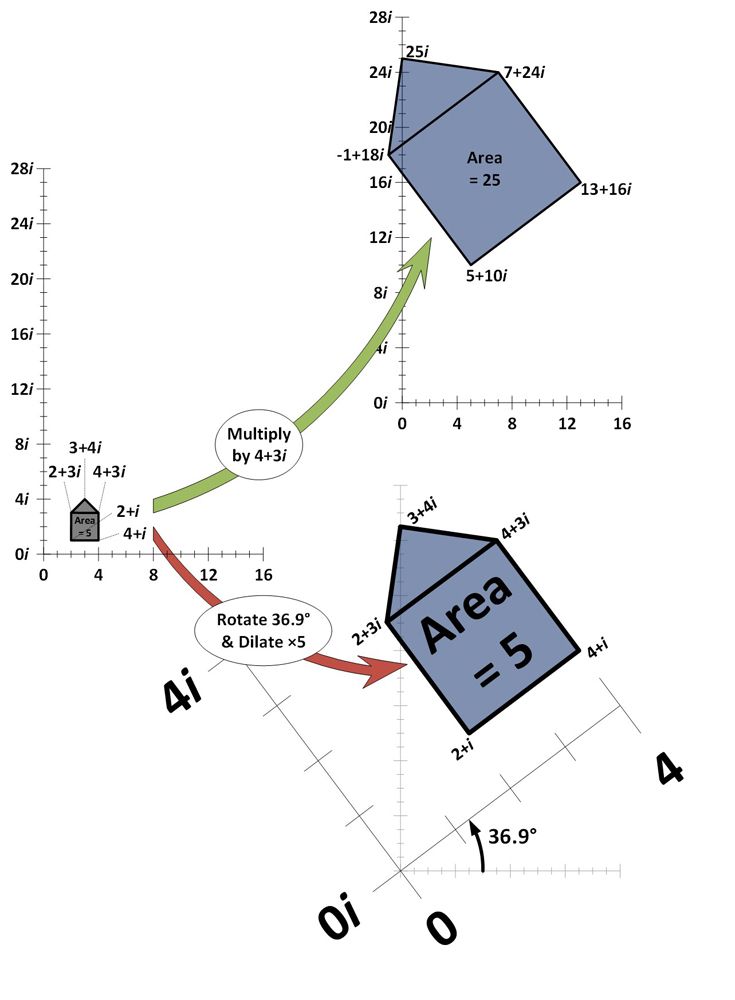
Différentes quantités de dilatation et de rotation peuvent produire les effets de la multiplication par n’importe quel nombre sur le plan complexe.
Forme polaire des nombres complexes
La quantité de rotation et de dilatation est déterminée par des propriétés intrinsèques au nombre 4+3i, qui, comme on le voit dans la figure ci-dessous, est à cinq unités de l’origine (r = 5) et forme un angle de 36,9 degrés avec l’axe horizontal (φ = 36,9°). Ces mesures sont utilisées dans ce que l’on appelle la forme polaire d’un nombre complexe (reiφ) par opposition à la forme rectangulaire normale (a+bi).
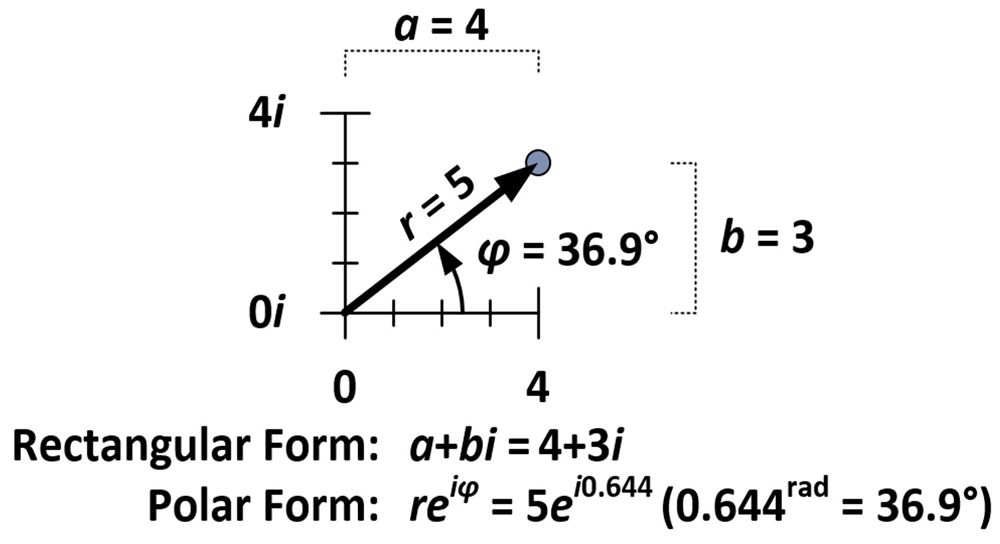
La forme polaire exige que φ soit mesuré en radians. Un radian (1rad) correspond à environ 57,3 degrés ; c’est la mesure de l’angle fait lorsque le rayon d’un cercle est enroulé contre la circonférence de ce cercle. Une mesure de π radians enveloppe la moitié d’un cercle ; une mesure de 2π radians enveloppe un cercle complet.
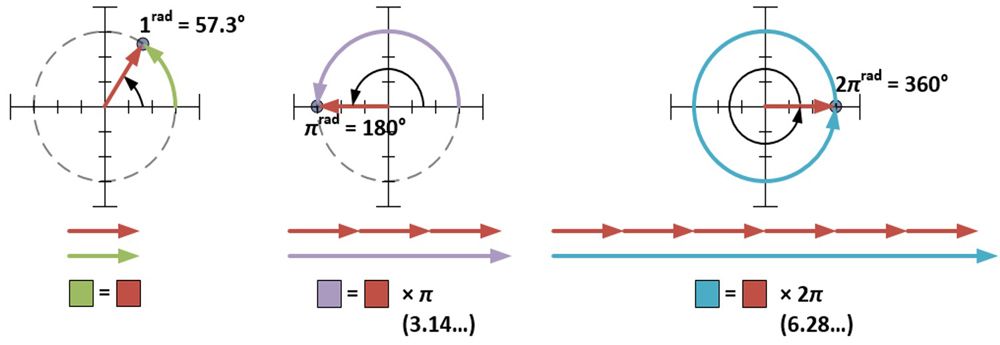
La mesure de l’angle pour 4+3i est de 0,644 radians (36,9° = 0,644rad) ce qui signifie que la forme polaire de 4+3i est 5ei0,644. Les mesures de r et φ peuvent également être déterminées pour chacun des points en forme de maison, et une autre façon d’obtenir l’effet de dilatation/rotation de la multiplication par 4+3i est de multiplier chaque r par cinq, et d’ajouter 36,9 degrés (ou 0,644rad) à chaque φ. D’après cette démonstration, nous voyons que lorsque des nombres complexes sont multipliés ensemble, les distances se multiplient et les angles s’additionnent. Cela est dû à une propriété intrinsèque aux exposants, qui peut être montrée algébriquement.
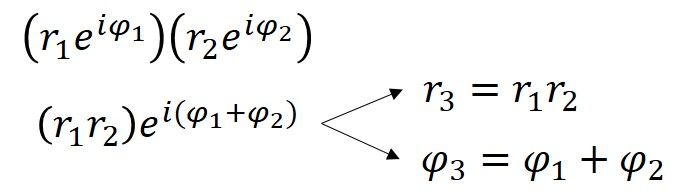
Avec la forme polaire des nombres complexes établie, la question de l’identité d’Euler est simplement un cas particulier de a+bi pour a = -1 et b = 0. Par conséquent pour la forme polaire reiφ, cela fait r= 1 et φ = π (puisque πrad = 180°).
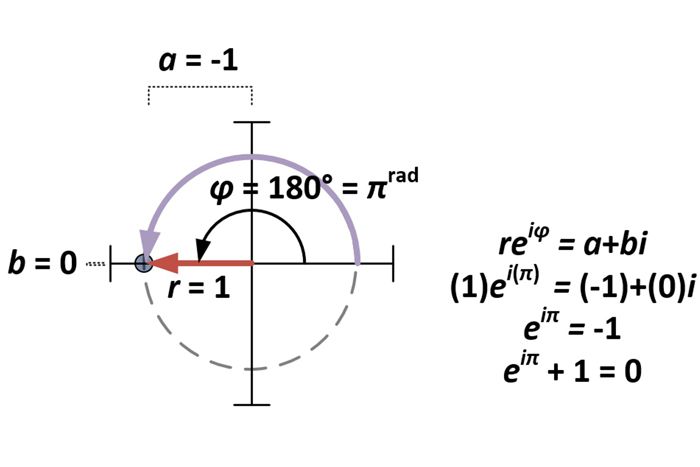
Dérivation de la forme polaire
Bien que l’Identité d’Euler découle de la forme polaire des nombres complexes, il est impossible de dériver la forme polaire (en particulier l’apparition spontanée du nombre e) sans calcul.
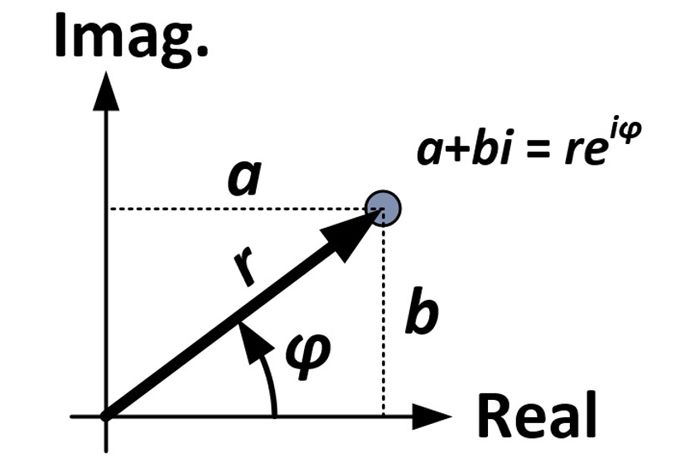
Nous commençons par la forme rectangulaire d’un nombre complexe :
a + bi
À partir du diagramme et de la trigonométrie, nous pouvons effectuer les substitutions suivantes :
(r-cosφ) + (r-sinφ)i
De là, nous pouvons factoriser r:
r-(cosφ + i-sinφ)
Parfois, « cosφ + i-sinφ » est nommé cisφ, ce qui est un raccourci pour « cosinus plus sinus imaginaire. »
r-cisφ
La fonction cisφ s’avère être égale à eiφ. C’est la partie impossible à démontrer sans calcul. Deux dérivations sont montrées ci-dessous:

Ainsi, l’équation r-cisφ s’écrit sous la forme polaire standard r-eiφ.