Eulers identitet er en lighed, der findes i matematikken, og som er blevet sammenlignet med en sonet fra Shakespeare og beskrevet som “den smukkeste ligning”. Det er et specialtilfælde af en grundlæggende ligning i kompleks aritmetik kaldet Eulers formel, som den afdøde store fysiker Richard Feynman i sine foredrag kaldte “vores juvel” og “den mest bemærkelsesværdige formel i matematikken”.
I et interview med BBC sagde professor David Percy fra Institute of Mathematics and its Applications, at Eulers identitet var “en ægte klassiker, og man kan ikke gøre det bedre end det … Den er enkel at se på og alligevel utrolig dybtgående, den omfatter de fem vigtigste matematiske konstanter.”
Eulers Identitet skrives simpelt som: eiπ + 1 = 0
De fem konstanter er:
- Tallet 0.
- Tallet 1.
- Tallet π, et irrationelt tal (med uendelige cifre), som er forholdet mellem omkredsen af en cirkel og dens diameter. Det er ca. 3,14159…
- Tallet e, som også er et irrationelt tal. Det er basen for naturlige logaritmer, der opstår naturligt ved studiet af sammensatte renter og beregning. Tallet e gennemsyrer matematikken og optræder tilsyneladende fra ingen steder i et stort antal vigtige ligninger. Det er ca. 2,71828….
- Tallet i, der er defineret som kvadratroden af negativ et: √(-1). Det mest fundamentale af de imaginære tal, der kaldes sådan, fordi intet tal i virkeligheden kan multipliceres med sig selv for at give et negativt tal (og derfor har negative tal ingen reelle kvadratrødder). Men i matematik er der mange situationer, hvor man er tvunget til at tage kvadratroden af et negativt tal. Bogstavet i bruges derfor som en slags stand-in til at markere steder, hvor dette er sket.
Fremgangsrig matematiker
Leonhard Euler var en schweiziskfødt matematiker fra det 18. århundrede, som udviklede mange begreber, der er en integreret del af den moderne matematik. Han tilbragte det meste af sin karriere i Sankt Petersborg i Rusland. Han var en af de mest produktive matematikere gennem tiderne, ifølge U.S. Naval Academy (USNA), med 886 udgivne artikler og bøger. En stor del af hans produktion kom i løbet af de sidste to årtier af hans liv, hvor han var fuldstændig blind. Der blev arbejdet så meget, at Sankt Petersborg-akademiet fortsatte med at udgive hans arbejde posthumt i mere end 30 år.
Eulers vigtige bidrag omfatter Eulers formel og Eulers sætning, som begge kan betyde forskellige ting afhængigt af sammenhængen. Ifølge USNA er der i mekanikken “Eulers vinkler (til at angive orienteringen af et stift legeme), Eulers sætning (at enhver rotation har en akse), Eulers ligninger for væskers bevægelse og Euler-Lagrange-ligningen (der stammer fra variationskalkulen).”
Multiplikation af komplekse tal
Eulers identitet stammer naturligt fra interaktioner af komplekse tal, som er tal, der består af to dele: et reelt tal og et imaginært tal; et eksempel er 4+3i. Komplekse tal optræder i et væld af anvendelser som f.eks. bølgemekanik (et studie inden for kvantemekanikken) og design af kredsløb, der anvender vekselstrøm (en almindelig praksis inden for elektroteknik). Desuden har komplekse tal (og deres fætre, de hyperkomplekse tal) en egenskab, der gør dem særligt nyttige til undersøgelse af computergrafik, robotteknik, navigation, flydynamik og kredsløbsmekanik: hvis man multiplicerer dem sammen, får man dem til at rotere. Denne egenskab vil hjælpe os med at forstå ræsonnementet bag Eulers identitet.
I eksemplet nedenfor er fem komplekse tal plottet på det komplekse plan og danner sammen en “husform”. Det komplekse plan svarer til en tallinje, bortset fra at det er todimensionalt. Den vandrette retning repræsenterer de reelle tal, og den lodrette akse repræsenterer de imaginære tal. Hvert komplekst tal i husform multipliceres med det komplekse tal 4+3i og plottes igen (grøn pil).
Som det fremgår, resulterer multiplikation med 4+3i i, at husformen udvides (øges i areal og bevæger sig lige meget væk fra oprindelsen 0+0i) og roterer (bliver skråt med en vis vinkel). For at vise, at dette netop er effekten af at gange med 4+3i, vises også effekten af at zoome fem gange ind på huset og dreje det 36,9 grader (rød pil). Der fremkommer nøjagtig den samme effekt.
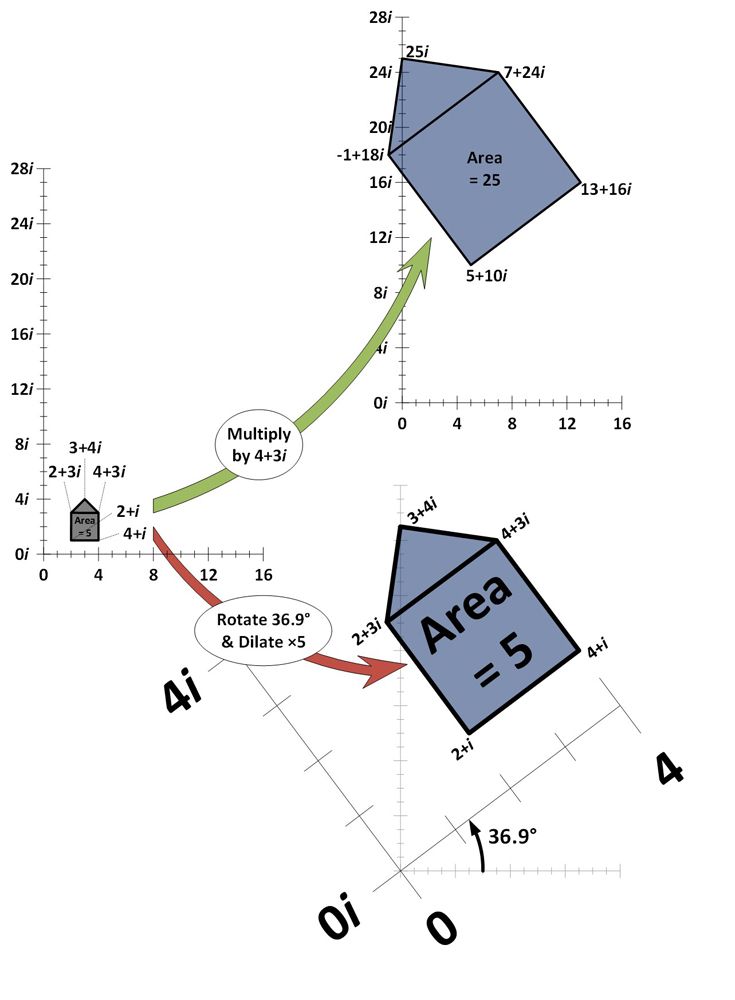
Differentierede mængder af dilatation og rotation kan producere virkningerne af multiplikation med et hvilket som helst tal i det komplekse plan.
Komplekse tals polære form
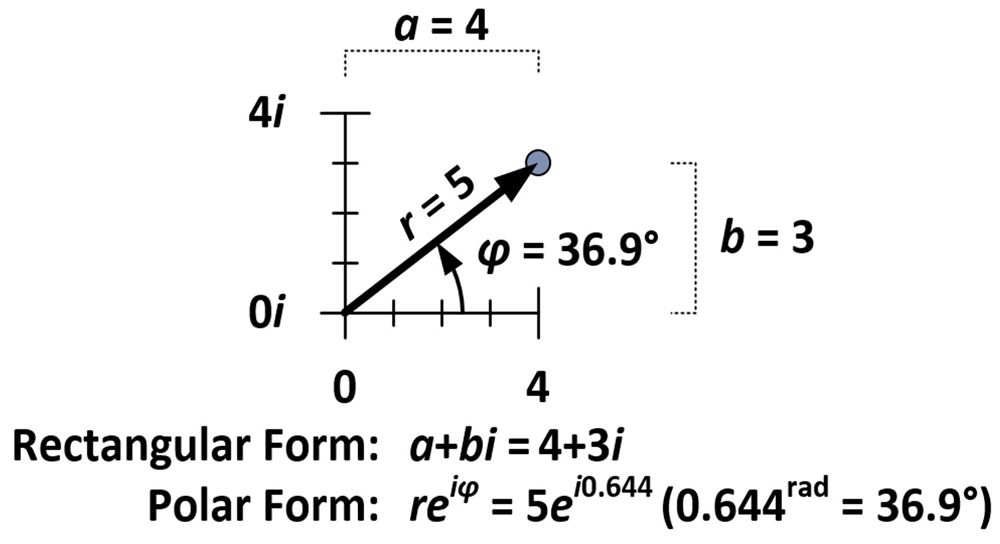
Mængden af rotation og dilatation bestemmes af egenskaber, der er indbygget i tallet 4+3i, der, som det ses i figuren nedenfor, er fem enheder fra oprindelsen (r = 5) og danner en vinkel på 36,9 grader med den horisontale akse (φ = 36,9°). Disse mål anvendes i det, der er kendt som den polære form af et komplekst tal (reiφ) i modsætning til den normale rektangulære form (a+bi).
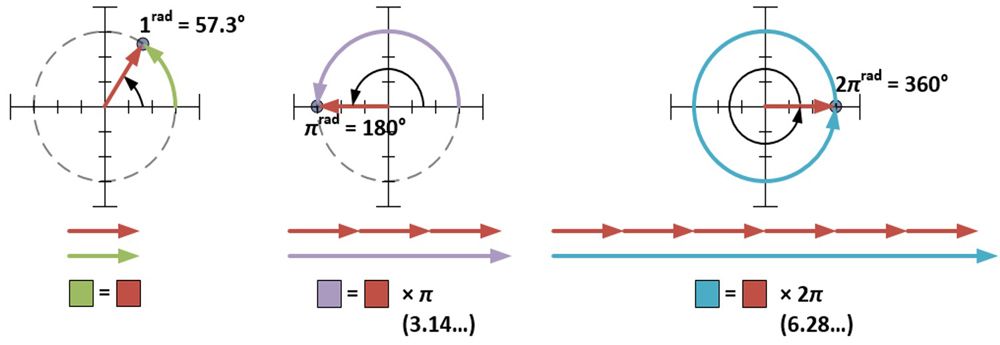
Den polære form kræver, at φ måles i radianer. En radian (1rad) er ca. 57,3 grader; det er det mål for den vinkel, der dannes, når en cirkels radius vikles mod denne cirkels omkreds. Et mål på π radianer omslutter halvdelen af en cirkel; et mål på 2π radianer omslutter en hel cirkel.
Vinkelmålet for 4+3i er 0,644 radianer (36,9° = 0,644rad), hvilket betyder, at den polære form af 4+3i er 5ei0,644. Målene for r og φ kan også bestemmes for hvert af de husformede punkter, og endnu en måde at opnå den udvidende/roterende effekt af multiplikation med 4+3i på er at gange hvert r med fem og tilføje 36,9 grader (eller 0,644rad) til hvert φ. Af denne demonstration kan vi se, at når komplekse tal multipliceres sammen, multipliceres afstandene og vinklerne lægges sammen. Dette skyldes en egenskab, der er indbygget i eksponenter, og som kan vises algebraisk.
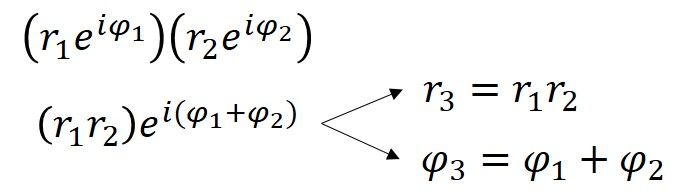
Med polærformen af komplekse tal fastlagt er spørgsmålet om Eulers identitet blot et specialtilfælde af a+bi for a = -1 og b = 0. For polarformen reiφ giver det følgelig r = 1 og φ = π (da πrad = 180°).
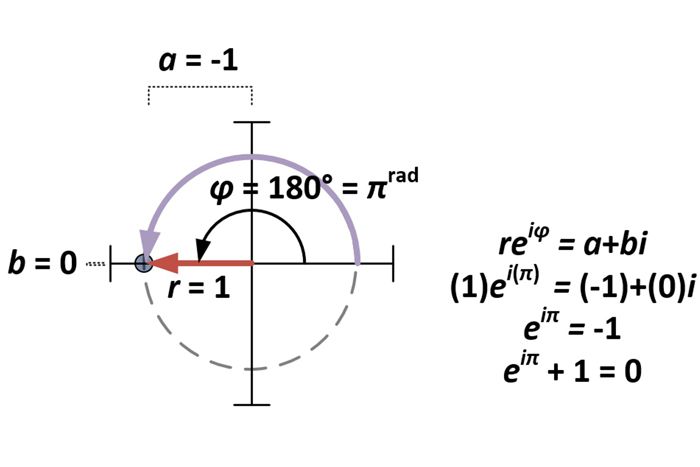
Afledning af polarform
Selv om Eulers Identitet følger af polarformen for komplekse tal, er det umuligt at aflede polarformen (især den spontane fremkomst af tallet e) uden beregning.
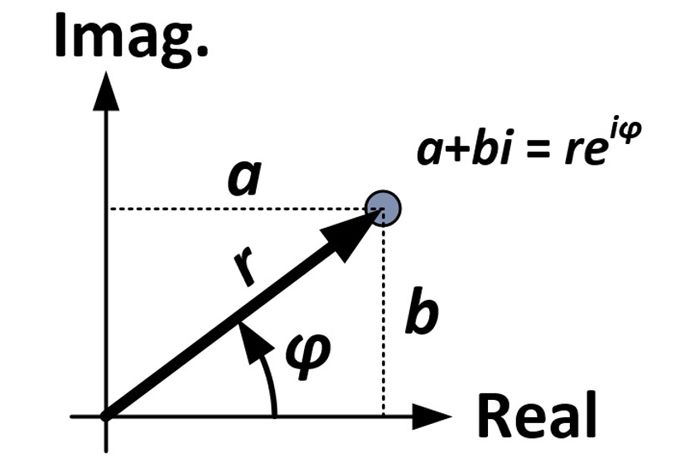
Vi starter med den rektangulære form af et komplekst tal:
a + bi
Fra diagrammet og trigonometrien kan vi foretage følgende substitutioner:
(r-cosφ) + (r-sinφ)i
Herfra kan vi faktorisere r:
r-(cosφ + i-sinφ)
I nogle tilfælde kaldes “cosφ + i-sinφ” for cisφ, hvilket er en forkortelse for “cosinus plus imaginær sinus”.”
r-cisφ
Funktionen cisφ viser sig at være lig med eiφ. Dette er den del, der er umulig at vise uden beregning. To afledninger er vist nedenfor:

Sådan skrives ligningen r-cisφ i den polære standardform r-eiφ.