Was ist Frequenz? Frequenz ist „wie oft“ etwas passiert. Da es sich bei Schall um Schwingungen handelt, verwenden wir die Frequenz, um zu beschreiben, wie oft etwas schwingt.Die Frequenz wird in Hertz (Hz) gemessen, was einfach bedeutet, wie oft pro Sekunde etwas schwingt. Eine „vollständige“ Schwingung wird als „Zyklus“ bezeichnet, gemessen an einem vollen Scheitel- und Tiefpunkt einer Welle (d. h. dem maximalen Abstand oder der „Amplitude“ über dem Mittel- oder „0“-Punkt, dargestellt auf der x-Achse). (In den frühen Tagen der elektronischen Musik wurde der Begriff „Zyklen pro Sekunde“ anstelle von Hz verwendet, den man heute auf vielen alten Synthesizern sehen kann).
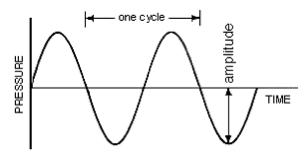
Das obige Bild ist eine Sinuswelle – die reinste Darstellung einer einzelnen Frequenz oder Schwingung. Die Zeit, die die Welle braucht, um einen Zyklus zu vollenden, ist die Frequenz der Welle (wieder, „wie oft“ sie schwingt). Mehr Schwingungen pro Sekunde (d. h. schnellere Schwingungen) erzeugen „höhere“ klingende Frequenzen und weniger Schwingungen pro Sekunde (d. h. langsamere Schwingungen) erzeugen „niedrigere“ klingende Frequenzen. Der Mensch kann nur Frequenzen zwischen 20Hz – 20.000Hz (20kHz) hören (mehr dazu siehe https://en.wikipedia.org/wiki/Hearing_range).
In der Musik sind die Begriffe Frequenz, Tonhöhe und Ton verwandt.Ein Ton ist ein Klang mit einer oder mehreren identifizierbaren Frequenzen. Die Frequenz ist die empirische Messung eines physikalischen Phänomens, definiert als die Anzahl der Schwingungen pro Sekunde. Die Tonhöhe ist eine subjektive Wahrnehmung der relativen Höhe eines Tons, wie z. B. „hoch“ oder „tief“ (mehr dazu siehe Conceptual Modelsand Cross-Domain Mapping von Lawerence Zbikowskihttp://zbikowski.uchicago.edu/pdfs/ZbikowskiConceptualmodels_1997.pdf).
Während Frequenzen mit Zahlen (Hz) dargestellt werden, wird die Tonhöhe mit Buchstaben dargestellt. Wenn Sie zum Beispiel jemals ein Orchester zu Beginn eines Konzerts „stimmen“ gehört haben, spielt ein einzelner Spieler (normalerweise eine Oboe oder Geige) ein „A“, das mit 440 Hz gemessen wird (bezeichnet als A440). Bei der Tonhöhe verwenden wir nur die Buchstaben A, B, C, D, E, F und G (zusätzliche Symbole werden verwendet, um sie zu erhöhen oder zu senken, mehr dazu später). Diese Tonhöhen wiederholen sich alle 8 Töne, was als Oktave bezeichnet wird. Um zu unterscheiden, auf welche Oktaven wir uns beziehen, wenn wir über die Tonhöhe sprechen, wird nach dem Buchstaben eine Zahl hinzugefügt. Zum Beispiel wird A440(Hz) als A4 in Bezug auf die Tonhöhe bezeichnet. Aber nicht verwirren lassen, die 4 bezieht sich auf die Oktave, in der wir uns auf dieses bestimmte A (speziell auf dem Klavier) beziehen – es ist nur ein Zufall, dass die Frequenz zufällig 440 ist, die 4 bezieht sich nicht speziell darauf. Aber warum ist A4 dann 440 Hz, werden Sie sich fragen… Nun, darauf gibt es eine ziemlich komplizierte Antwort, aber letztlich ist es tatsächlich willkürlich. Einfach ausgedrückt: Im 19. Jahrhundert haben sich ein paar Leute zusammengetan und beschlossen, dass dies der Fall ist. (Wenn Sie mehr über das Thema wissen möchten, recherchieren Sie unter A440 oder Tonhöhen-/Stimmstandardshttps://en.wikipedia.org/wiki/A440(pitchstandard)).
Es ist wichtig zu wissen, dass die Frequenz absolut ist, während die Tonhöhe relativ ist (diese relativen Änderungen werden als „Stimmung“ bezeichnet). Wir verwenden Tonhöhen, um ihre Beziehung (d.h. ihr Verhältnis) zu anderen Tonhöhen zu beschreiben, und die Analyse dieser Beziehungen ist die Grundlage der „Musiktheorie“. Im Allgemeinen haben wir uns darauf geeinigt, dass A4 als diejenige Tonhöhe definiert wird, deren Frequenz 440 Hz beträgt (eine absolute Referenz). Wir können dann die „Tonhöhe“ oder „Stimmung“ aller anderen Noten im Verhältnis zu dieser mit Hilfe einer bestimmten Stimmformel bestimmen.
Ein sehr wichtiger Aspekt der gesamten Musiktheorie ist, dass Oktaven speziell als „Verdoppelung“ oder „Halbierung“ der Frequenz einer Tonhöhe definiert werden. Zum Beispiel sind die Frequenzen 220 Hz, 440 Hz und 880 Hz alle A’s, aber in verschiedenen Oktaven: A3, A4 bzw. A5. In der westlichen Musiktheorie haben wir uns im Allgemeinen (und offen gesagt willkürlich) darauf geeinigt, dass es innerhalb jeder Oktave 12 gleiche Unterteilungen oder Tonhöhen gibt. Wie können wir also bestimmen, wo diese anderen Noten im Verhältnis zu A440 „gestimmt“ sind? Nun, nach vielen Jahren des Experimentierens kam man zu dem Schluss, dass die folgende Formel das relative Verhältnis zwischen den Tonhöhen bestimmt (genauer gesagt, die Frequenz f der n-ten Taste auf einem Standardklavier):
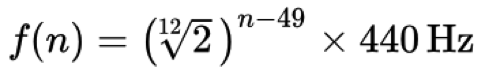https://en.wikipedia.org/wiki/Pianokeyfrequencies
Einfach ausgedrückt, wird jeder Ton/Tonhöhe in der westlichen klassischen Musikstimmung abgeleitet, indem man mit A440 als „Referenzton“ beginnt und dann mit der zwölften Wurzel aus zwei (~1,059463) multipliziert oder dividiert, um einen anderen Ton über oder unter diesem Referenzton zu erhalten. Die Zahl 49 ist in diesem Fall willkürlich (A4 ist die 49. Taste auf einer Standardklaviertastatur) und in der Computermusik verwenden wir normalerweise MIDI-Nummern für unsere Berechnungen – A440 ist zum Beispiel die MIDI-Tastennummer 69 (mehr über MIDI-Standards in einer separaten Lektion).
Es sollte beachtet werden, dass diese Formel nur einen bestimmten Stil der „Stimmung“ repräsentiert, der innerhalb der westlichen klassischen Musiktradition existiert und im Allgemeinen als „Weltstandard“ verwendet wird, wenn man über Tonhöhen/Frequenz/Tonhöhen-Beziehungen im Allgemeinen spricht, obwohl diese Beziehungen willkürlich sind und andere Stimmsysteme innerhalb verschiedener Kulturen und Traditionen existieren.Dieses System behält eine wichtige „Regel“ bei, die besagt, dass Oktaven als exakte Verdoppelung oder Halbierung von Frequenzen definiert werden, während die gleichen (Tonhöhen-)Verhältnisse beibehalten werden, indem jede Oktave in 12 gleiche Teile unterteilt wird. Wir nennen dieses Stimmsystem 12-Ton-Gleichschwebungs-Temperament und es dient als Grundlage für den größten Teil der Welt als grundlegendes und vereinbartes Stimmsystem, insbesondere wenn es um die Standardisierung von elektronischen Musikgeräten geht. (Alle Klaviere sind in diesem System gestimmt und alle MIDI-Daten folgen diesem allgemeinen Prinzip).
In der Musikterminologie beschreiben wir Tonhöhen (oder Töne) als auf- oder absteigend in Form von „Schritten“. Es gibt zwei Arten von Schritten: Halbtonschritte und Ganztonschritte (auch Halbtöne oder Ganztöne genannt).Das Anheben von Tönen um einen Halbtonschritt (d.h. einen Halbton) wird mit einem ♯Symbol, dem so genannten „sharp“ (Zahlen- oder Hashtag-Symbol), und das Absenken von Tönen um einen Halbtonschritt mit einem ♭-Symbol, dem so genannten „flat“ (häufig wird auch ein kleines „b“ verwendet), angegeben. Man kann sich Halbtöne oder Halbtonschritte als den Mindestabstand zwischen zwei benachbarten Klaviertasten oder Gitarrenbünden vorstellen.
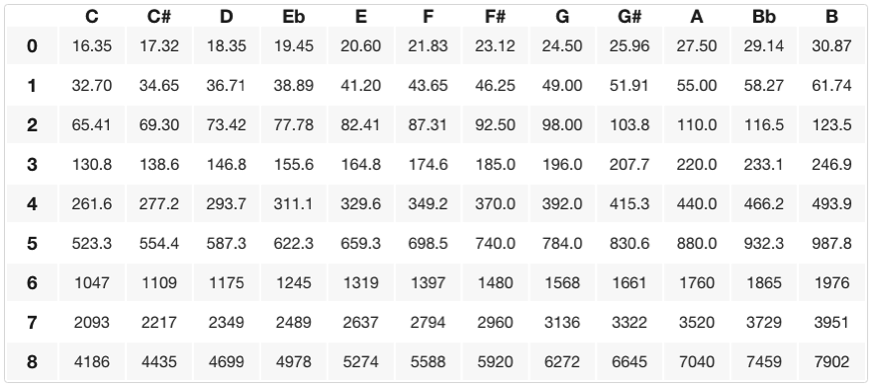
Um die Frequenz einen Halbton höher als A4 zu erhalten, multiplizieren wir 440 Hz mit der Zwölftelwurzel von zwei und erhalten ~466,2 Hz, was uns ein A# (oder Bb) gibt. A# und Bb werden als „enharmonische Noten“ bezeichnet, d. h. Tonhöhen, die technisch gesehen dieselbe Frequenz haben, aber je nach Tonart oder musikalischem Kontext unterschiedlich „geschrieben“ werden können (mehr dazu in einer anderen Lektion). Um die Frequenz einen ganzen Schritt höher als A4 zu erhalten, können wir 440 Hz zweimal mit der zwölften Wurzel aus zwei multiplizieren, was uns ~493,9 Hz oder B4 ergibt. Unten ist eine Tabelle mit allen spezifischen Frequenzen und ihrer Tonhöhe/Oktave-Beziehung (Notennamen auf der x-Achse und Oktavzahlen auf der y-Achse).
https://www.seventhstring.com/resources/notefrequencies.html
Diese Sammlung von „zwölf Noten pro Oktave“ wird chromatische Tonleiter genannt. Eine chromatische Tonleiter beginnt auf einer beliebigen Tonhöhe und steigt (oder sinkt) um 11 aufeinander folgende Halbtonschritte (Halbtöne) von der Grundtonhöhe aus. In der obigen Tabelle kannst du die spezifischen Frequenzen oder Noten/Tonhöhen jeder chromatischen Tonleiter finden, indem du bei einer bestimmten Note (dem Grundton) beginnst und 11 Halbtöne (benachbarte Tonhöhen) aufwärts oder abwärts zählst.
Wie du bemerkt hast, werden einige der Noten in der obigen Tabelle mit einem # (scharf) geschrieben, während andere mit einem b (flach) geschrieben werden. Theoretisch kann jede Note um einen halben oder ganzen Schritt/Ton erhöht oder erniedrigt werden, indem man eines dieser Symbole anfügt. Aufgrund der weit verbreiteten und vorhersehbaren Praktiken der westlichen Musiktheorie gibt es jedoch Konventionen, dass bestimmte Noten auf eine bestimmte Weise „geschrieben“ werden. Was die „enharmonischen Schreibweisen“ von Noten und Tonhöhen angeht (Noten mit gleicher Frequenz, aber unterschiedlichen Tonhöhen), so stellt die obige Tabelle die gängigsten Schreibweisen von Noten und Tonhöhen im Hinblick auf die traditionelle Praxis der „Tonart“ in der Musik dar, enthält aber nicht alle Möglichkeiten. Die folgenden Noten sind gängige enharmonische Schreibweisen (Schrägstriche zeigen an, dass die Noten/Tonhöhen dieselbe Frequenz haben, aber als unterschiedliche Tonhöhen dargestellt oder „geschrieben“ werden können):
C#/Db D#/Eb F#/Gb G#/Ab A#/Bb
Natürlich kann theoretisch jede Note mit einem #- oder b-Symbol um einen Halbton oder sogar einen Ganzton erhöht oder erniedrigt werden, und etwas fortgeschrittenere Musiktheorie befasst sich mit den so genannten Doppelbögen und -tönen.Ohne zu kompliziert zu werden oder in die Tiefe zu gehen, sind alle Tonleitern oder musikalischen Tonarten eine Sammlung von Halbtonschritten und Ganztonschritten, und die Schreibweise dieser Tonhöhen gibt dem Interpreten Hinweise auf die Beziehungen (d.h. Verhältnisse) zwischen den vom Komponisten verwendeten Tonhöhen.
- Hertz (Hz)
- Frequenz
- Tonhöhe
- Tonhöhe
- A4 (A440)
- Oktaven
- Ganzschritte (Ganztöne)
- Halbtonschritte (Halbtöne)
Selbst-Quiz
- Der Ton G3 hat eine Grundfrequenz von 196 Hz. Wie lauten die Frequenzen der Tonhöhen G2 und G4 (eine Oktave unter und über G4), ohne eine Tabelle zu Rate zu ziehen?
Zusätzliche Hilfsmittel
- Schalleigenschaften – Khan Academy
- Schall: Crashkurs Physik