Lassen Sie uns untersuchen, was passiert, wenn negative Werte unter dem Radikalsymbol (als Radikand) für Kubikwurzeln und Quadratwurzeln erscheinen.
In manchen Situationen sind negative Zahlen unter einem Radikalsymbol in Ordnung. Zum Beispiel ist 
kein Problem, da (-2) – (-2) – (-2) = -8 ist, was die Antwort -2 ergibt. Bei Würfelwurzelproblemen ist es möglich, einen negativen Wert dreimal mit sich selbst zu multiplizieren und eine negative Antwort zu erhalten.
Schwierigkeiten entstehen jedoch, wenn wir ein Problem wie 
betrachten. Bei diesem Quadratwurzelproblem wird nach einer Zahl gefragt, die mit sich selbst multipliziert ein Produkt (Antwort) von -16 ergibt. Es gibt einfach keine Möglichkeit, eine Zahl mit sich selbst zu multiplizieren und ein negatives Ergebnis zu erhalten. Überlegen Sie: (4) – (4) = 16 und (-4) – (-4) = 16.
|
Kubuswurzeln:
 |
Aber
|
Quadratwurzeln:
 |
|
Ja, (-2) x (-2) x (-2) = -8.
Kein Problem. |
Nein! (4) x (4) ≠ -16. |
Quadratwurzeln sind die Übeltäter! Die Schwierigkeiten entstehen, wenn man einen negativen Wert unter einer Quadratwurzel findet. Es ist nicht möglich, einen Wert zu quadrieren (ihn mit sich selbst zu multiplizieren) und dabei einen negativen Wert zu erhalten. Was ist also zu tun?
 |
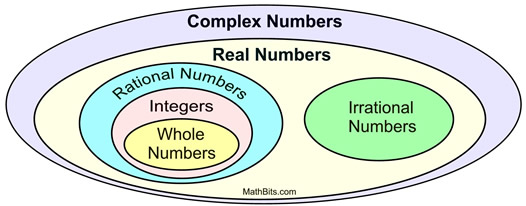
Die Quadratwurzel einer negativen Zahl gibt es in der Menge der reellen Zahlen nicht.
|
Als Probleme mit negativen Werten unter einer Quadratwurzel zum ersten Mal auftauchten, dachten die Mathematiker, dass es keine Lösung gibt. Sie sahen Gleichungen wie x2 + 1 = 0 und fragten sich, was die Lösung 
wirklich bedeutete.
In dem Bemühen, dieses Problem zu lösen, „schufen“ die Mathematiker eine neue Zahl, i, die als „imaginäre Zahl“ bezeichnet wurde, da sie nicht in der Menge der „Reellen Zahlen“ enthalten war. Diese neue Zahl wurde mit viel Skepsis betrachtet. Die imaginäre Zahl erschien erstmals im Jahr 1545 im Druck.
 |
Die imaginäre Zahl „i“ ist die Quadratwurzel aus minus eins. |
Eine imaginäre Zahl besitzt die einzigartige Eigenschaft, dass das Ergebnis negativ ist, wenn man es quadriert.
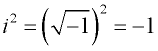
Betrachte: 
Das Verfahren zur Vereinfachung eines Radikals, das einen negativen Faktor enthält, ist dasselbe wie die normale Radikalvereinfachung. Der einzige Unterschied ist, dass das 
durch ein „i“ ersetzt wird.
Als die Forschung mit imaginären Zahlen fortgesetzt wurde, entdeckte man, dass sie tatsächlich eine Lücke in der Mathematik füllten und einen nützlichen Zweck erfüllten. Imaginäre Zahlen sind für das Studium von Wissenschaften wie Elektrizität, Quantenmechanik, Schwingungsanalyse und Kartographie unerlässlich.
Als das imaginäre i mit der Menge der reellen Zahlen kombiniert wurde, entstand die allumfassende Menge der komplexen Zahlen.
