Tarkastellaan, mitä tapahtuu, kun negatiiviset arvot esiintyvät radikaalisymbolin alla (radikaattina) kuutio- ja neliöjuurille.
Jossain tilanteissa negatiiviset luvut radikaalisymbolin alla ovat OK. Esimerkiksi 
ei ole ongelma, koska (-2) – (-2) – (-2) = -8, jolloin vastaus on -2. Kuutiojuuriongelmissa on mahdollista kertoa negatiivinen arvo kolme kertaa itsellään ja saada negatiivinen vastaus.
Vaikeuksia syntyy kuitenkin, kun tarkastelemme 
kaltaista ongelmaa. Tässä neliöjuuritehtävässä kysytään lukua kerrottuna itsellään, joka antaa tulokseksi (vastaukseksi) -16. Ei yksinkertaisesti ole mitään tapaa kertoa luku kertaa itsensä ja saada negatiivinen tulos. Mieti asiaa: (4) – (4) = 16 ja (-4) – (-4) = 16.
|
Kuutiojuuret:
 |
MUTTA
|
NELIPUOLISET JUURET:
 |
|
Niin, (-2) x (-2) x (-2) = -8.
Ei ongelmaa. |
Ei! (4) x (4) ≠ -16. |
Neliöjuuret ovat syyllisiä! Vaikeuksia syntyy, kun neliöjuuren alla on negatiivinen arvo. Ei ole mahdollista neliöidä arvoa (kertoa se kertaa itsensä) ja saada tulokseksi negatiivinen arvo. Mitä siis tehdään?
 |
Negatiivisen luvun neliöjuurta ei ole olemassa reaalilukujen joukossa.
|
Kun neliöjuuren alle jääviin negatiivisiin arvoihin liittyvät ongelmat ilmaantuivat ensimmäisen kerran, matemaatikot ajattelivat, ettei ratkaisua ole olemassa. He näkivät yhtälöitä, kuten x2 + 1 = 0, ja ihmettelivät, mitä ratkaisu 
todella tarkoitti.
Tämän ongelman ratkaisemiseksi matemaatikot ”loivat” uuden luvun, i:n, jota kutsuttiin ”imaginaariluvuksi”, koska se ei kuulunut ”reaalilukujen” joukkoon. Tähän uuteen lukuun suhtauduttiin hyvin epäilevästi. Kuvitteellinen luku ilmestyi ensimmäisen kerran painettuna vuonna 1545.
 |
Kuvitteellinen luku ”i” on negatiivisen ykkösen neliöjuuri. |
Kuvituksellisella luvulla on se ainutkertainen ominaisuus, että kun se neliöityy, tulos on negatiivinen.
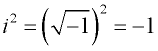
Harkitse: 
Negatiivisen tekijän sisältävän radikaalin yksinkertaistaminen on sama prosessi kuin normaali radikaalin yksinkertaistaminen. Ainoa ero on, että 
korvataan ”i ” -merkillä.
Kun mielikuvituslukujen tutkiminen jatkui, huomattiin, että ne itse asiassa täyttivät aukon matematiikassa ja niillä oli hyödyllinen tarkoitus. Mielikuvitusluvut ovat välttämättömiä esimerkiksi sähkön, kvanttimekaniikan, värähtelyanalyysin ja kartografian kaltaisten tieteiden tutkimuksessa.
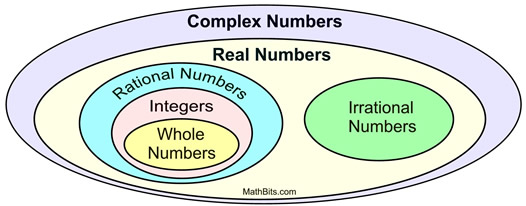
Kun mielikuvitusluku i yhdistettiin reaalilukujen joukkoon, syntyi kaiken kattava kompleksilukujen joukko.
